2020年济南市槐荫区中考数学一模 模拟试卷（含答案）

2020年济南市槐荫区中考数学一模 模拟试卷（含答案）

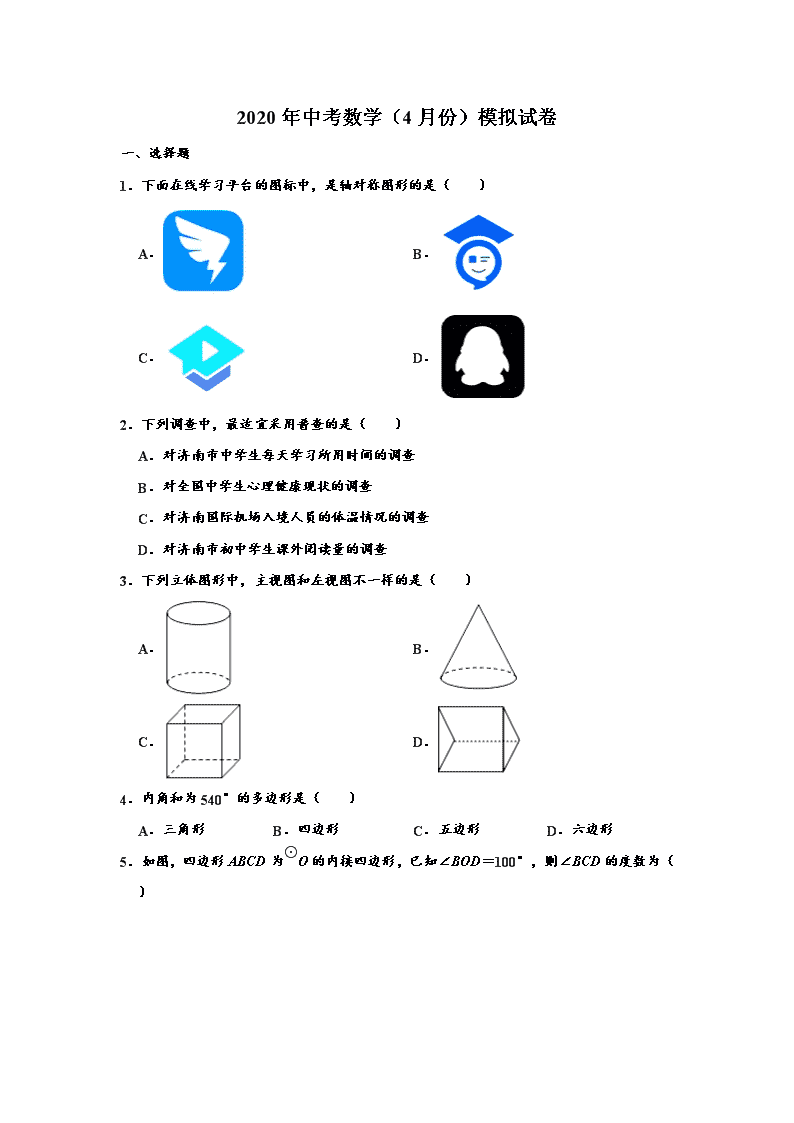
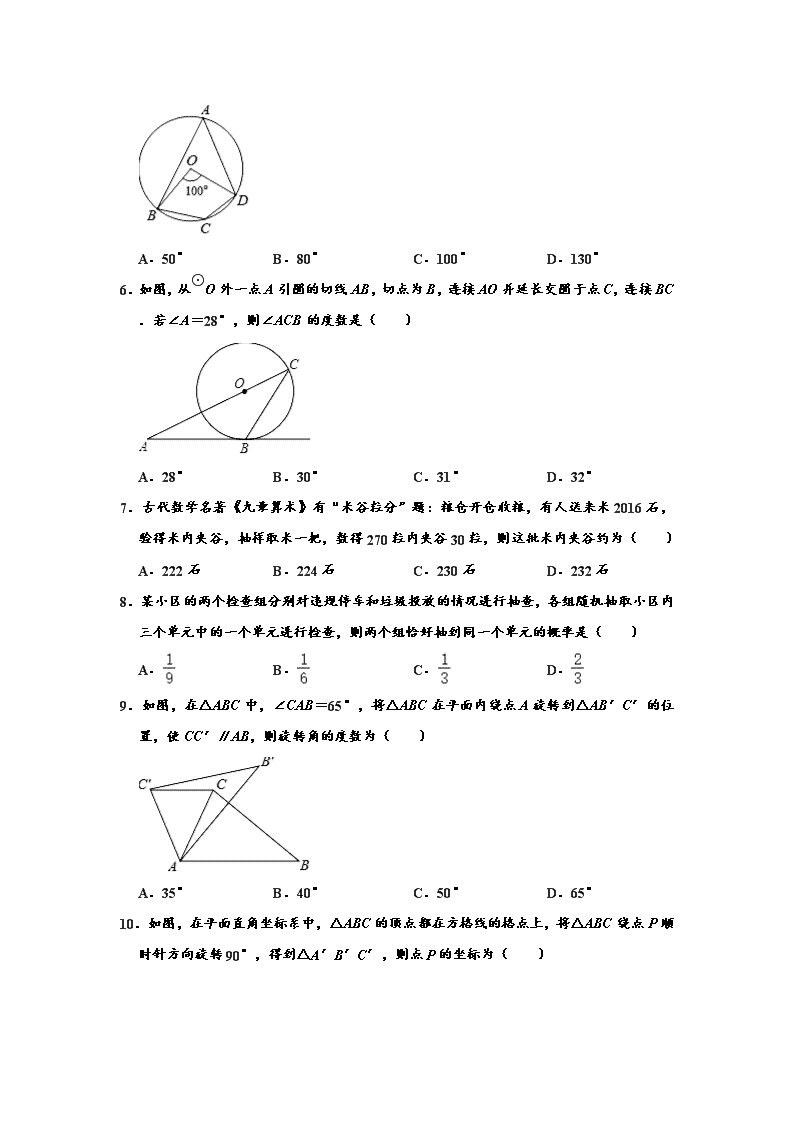
‎2020年中考数学（4月份）模拟试卷 一、选择题 ‎1．下面在线学习平台的图标中，是轴对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎2．下列调查中，最适宜采用普查的是（　　）‎ A．对济南市中学生每天学习所用时间的调查 ‎ B．对全国中学生心理健康现状的调查 ‎ C．对济南国际机场入境人员的体温情况的调查 ‎ D．对济南市初中学生课外阅读量的调查 ‎3．下列立体图形中，主视图和左视图不一样的是（　　）‎ A． B． ‎ C． D．‎ ‎4．内角和为540°的多边形是（　　）‎ A．三角形 B．四边形 C．五边形 D．六边形 ‎5．如图，四边形ABCD为⊙O的内接四边形，已知∠BOD＝100°，则∠BCD的度数为（　　）‎ A．50° B．80° C．100° D．130°‎ ‎6．如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC．若∠A＝28°，则∠ACB的度数是（　　）‎ A．28° B．30° C．31° D．32°‎ ‎7．古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米2016石，验得米内夹谷，抽样取米一把，数得270粒内夹谷30粒，则这批米内夹谷约为（　　）‎ A．222石 B．224石 C．230石 D．232石 ‎8．某小区的两个检查组分别对违规停车和垃圾投放的情况进行抽查，各组随机抽取小区内三个单元中的一个单元进行检查，则两个组恰好抽到同一个单元的概率是（　　）‎ A． B． C． D．‎ ‎9．如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（　　）‎ A．35° B．40° C．50° D．65°‎ ‎10．如图，在平面直角坐标系中，△ABC的顶点都在方格线的格点上，将△ABC绕点P顺时针方向旋转90°，得到△A′B′C′，则点P的坐标为（　　）‎ A．（0，4） B．（1，1） C．（1，2） D．（2，1）‎ ‎11．为了了解某校九年级学生的体能情况，随机抽查了该校九年级若干名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的直方图，请根据图示计算，仰卧起坐次数在25～30次的学生人数占被调查学生人数的百分比为（　　）‎ A．40% B．30% C．20% D．10%‎ ‎12．如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（　　）‎ A．（2，5） B．（5，2） C．（2，﹣5） D．（5，﹣2）‎ ‎13．为了解某班学生每天使用零花钱的情况，小敏随机调查了15名同学，结果如表：‎ 每天用零花钱（单位：元）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 人数 ‎2‎ ‎4‎ ‎5‎ ‎3‎ ‎1‎ 则这15名同学每天使用零花钱的众数和中位数分别是（　　）‎ A．3，3 B．5，2 C．3，2 D．3，5‎ ‎14．如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎15．如图，在矩形AOBC中，O为坐标原点，OA、OB分别在x轴、y轴上，点B的坐标为（0，3），∠ABO＝30°，将△ABC沿AB所在直线对折后，点C落在点D处，则点D的坐标为（　　）‎ A．（，） B．（2，） C．（，） D．（，3﹣）‎ ‎16．如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'＝1，则A'D等于（　　）‎ A．2 B．3 C． D．‎ ‎17．如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A、B、C、D不重合），经过P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为（　　）‎ A． B． C． D．‎ ‎18．如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S△PAB＝S矩形ABCD，则点P到A、B两点距离之和PA+PB的最小值为（　　）‎ A． B． C．5 D．‎ ‎19．如图，扇形AOB的半径为1，∠AOB＝90°，以AB为直径画半圆，则图中的阴影部分的面积为（　　）‎ A． B．π C．π D．π ‎20．如图，在Rt△ACB中，∠ACB＝90°，AC＝BC，点D是AB上的一个动点（不与点A，B重合），连接CD，将CD绕点C顺时针旋转90°得到CE，连接DE，DE与AC相交于点F，连接AE，则图中与△ACE全等或相似的三角形有（　　）‎ A．1个 B．2个 C．3个 D．4个 二、填空题（本大题共5个小题．每小题4分，共20分．把答案填在答题卡的横线上.）‎ ‎21．已知一个正n边形的每个内角都为144°，则边数n为　 　．‎ ‎22．如图，已知路灯离地面的高度AB为4.8m，身高为1.6m的小明站在D处的影长为2m，那么此时小明离电杆AB的距离BD为　 　m．‎ ‎23．一个不透明的口袋中共有8个白球、5个黄球、5个绿球、2个红球，这些球除颜色外都相同．从口袋中随机摸出一个球，这个球是白球的概率是　 　．‎ ‎24．如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD＝90°，CO＝CD，若B（1，0），则点C的坐标为　 　．‎ ‎25．如图，在正方形ABCD中，E是边AD的中点．将△ABE沿直线BE翻折，点A落在点F处，联结DF，那么∠EDF的正切值是　 　．‎ 参考答案 一、选择题（本大题共20个小题，每小题4分，共80分．在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1．下面在线学习平台的图标中，是轴对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴可得答案．‎ 解：A、不是轴对称图形，故此选项不合题意；‎ B、不是轴对称图形，故此选项不合题意；‎ C、不是轴对称图形，故此选项不合题意；‎ D、是轴对称图形，故此选项符合题意；‎ 故选：D．‎ ‎【点评】此题主要考查了轴对称图形，关键是掌握轴对称图形的概念．‎ ‎2．下列调查中，最适宜采用普查的是（　　）‎ A．对济南市中学生每天学习所用时间的调查 ‎ B．对全国中学生心理健康现状的调查 ‎ C．对济南国际机场入境人员的体温情况的调查 ‎ D．对济南市初中学生课外阅读量的调查 ‎【分析】直接利用抽样调查和全面调查的意义分别分析得出答案．‎ 解：A、对济南市中学生每天学习所用时间的调查，适合抽样调查，不合题意；‎ B、对全国中学生心理健康现状的调查，适合抽样调查，不合题意；‎ C、对济南国际机场入境人员的体温情况的调查，必须采用普查，符合题意；‎ D、对济南市初中学生课外阅读量的调查，适合抽样调查，不合题意；‎ 故选：C．‎ ‎【点评】此题主要考查了抽样调查和全面调查的意义，正确掌握相关定义是解题关键．‎ ‎3．下列立体图形中，主视图和左视图不一样的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】主视图、左视图是分别从物体正面、左面看，所得到的图形．‎ 解：A、圆柱的主视图和左视图均为全等的长方形，不符合题意；‎ B、圆锥的主视图和左视图均为全等的等腰三角形，不符合题意；‎ C、正方体的主视图和左视图均为全等的正方形，不符合题意；‎ D、这个三棱柱的主视图是正方形，左视图是三角形，符合题意；‎ 故选：D．‎ ‎【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图，左视图是从物体的左面看得到的视图．‎ ‎4．内角和为540°的多边形是（　　）‎ A．三角形 B．四边形 C．五边形 D．六边形 ‎【分析】n边形的内角和公式为（n﹣2）•180°，由此列方程求n．‎ 解：设这个多边形的边数是n，‎ 则（n﹣2）•180°＝540°，‎ 解得n＝5，‎ 故选：C．‎ ‎【点评】本题考查了多边形外角与内角．此题比较简单，只要结合多边形的内角和公式来寻求等量关系，构建方程即可求解．‎ ‎5．如图，四边形ABCD为⊙O的内接四边形，已知∠BOD＝100°，则∠BCD的度数为（　　）‎ A．50° B．80° C．100° D．130°‎ ‎【分析】首先根据圆周角与圆心角的关系，求出∠BAD的度数；然后根据圆内接四边形的对角互补，用180°减去∠BAD的度数，求出∠BCD的度数是多少即可．‎ 解：∵∠BOD＝100°，‎ ‎∴∠BAD＝100°÷2＝50°，‎ ‎∴∠BCD＝180°﹣∠BAD ‎＝180°﹣50°‎ ‎＝130°‎ 故选：D．‎ ‎【点评】（1）此题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，要熟练掌握．‎ ‎（2）此题还考查了圆内接四边形的性质，要熟练掌握，解答此题的关键是要明确：①圆内接四边形的对角互补． ②圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）．‎ ‎6．如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC．若∠A＝28°，则∠ACB的度数是（　　）‎ A．28° B．30° C．31° D．32°‎ ‎【分析】连接OB，如图，先根据切线的性质得到∠ABO＝90°，再利用互余计算出∠AOB＝62°，然后根据圆周角定理得到∠ACB的度数．‎ 解：连接OB，如图，‎ ‎∵AB为切线，‎ ‎∴OB⊥AB，‎ ‎∴∠ABO＝90°，‎ ‎∴∠AOB＝90°﹣∠A＝90°﹣28°＝62°，‎ ‎∴∠ACB＝∠AOB＝31°．‎ 故选：C．‎ ‎【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理．‎ ‎7．古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米2016石，验得米内夹谷，抽样取米一把，数得270粒内夹谷30粒，则这批米内夹谷约为（　　）‎ A．222石 B．224石 C．230石 D．232石 ‎【分析】用总数量乘以样本中谷所占比例即可得．‎ 解：这批米内夹谷约为2016×＝224（石），‎ 故选：B．‎ ‎【点评】本题主要考查用样本估计总体，从一个总体得到一个包含大量数据的样本，我们很难从一个个数字中直接看出样本所包含的信息．这时，我们用频率分布直方图来表示相应样本的频率分布，从而去估计总体的分布情况．‎ ‎8．某小区的两个检查组分别对违规停车和垃圾投放的情况进行抽查，各组随机抽取小区内三个单元中的一个单元进行检查，则两个组恰好抽到同一个单元的概率是（　　）‎ A． B． C． D．‎ ‎【分析】将三个小区分别记为A、B、C，列举出所有情况即可，看所求的情况占总情况的多少即可．‎ 解：将三个小区分别记为A、B、C，‎ 列表如下：‎ A B C A ‎（A，A）‎ ‎（B，A）‎ ‎（C，A）‎ B ‎（A，B）‎ ‎（B，B）‎ ‎（C，B）‎ C ‎（A，C）‎ ‎（B，C）‎ ‎（C，C）‎ 由表可知，共有9种等可能结果，其中两个组恰好抽到同一个小区的结果有3种，‎ ‎∴两个组恰好抽到同一个单元的概率是＝，‎ 故选：C．‎ ‎【点评】此题主要考查了列表法求概率，列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适用于两步或两步以上完成的事件；解题时还要注意是放回试验还是不放回试验．用到的知识点为：概率＝所求情况数与总情况数之比．‎ ‎9．如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（　　）‎ A．35° B．40° C．50° D．65°‎ ‎【分析】根据两直线平行，内错角相等可得∠ACC′＝∠CAB，根据旋转的性质可得AC＝AC′，然后利用等腰三角形两底角相等求∠CAC′，再根据∠CAC′、∠BAB′都是旋转角解答．‎ 解：∵CC′∥AB，‎ ‎∴∠ACC′＝∠CAB＝65°，‎ ‎∵△ABC绕点A旋转得到△AB′C′，‎ ‎∴AC＝AC′，‎ ‎∴∠CAC′＝180°﹣2∠ACC′＝180°﹣2×65°＝50°，‎ ‎∴∠CAC′＝∠BAB′＝50°．‎ 故选：C．‎ ‎【点评】本题考查了旋转的性质，等腰三角形两底角相等的性质，熟记性质并准确识图是解题的关键．‎ ‎10．如图，在平面直角坐标系中，△ABC的顶点都在方格线的格点上，将△ABC绕点P 顺时针方向旋转90°，得到△A′B′C′，则点P的坐标为（　　）‎ A．（0，4） B．（1，1） C．（1，2） D．（2，1）‎ ‎【分析】选两组对应点，连接后作其中垂线，两中垂线的交点即为点P．‎ 解：由图知，旋转中心P的坐标为（1，2），‎ 故选：C．‎ ‎【点评】本题主要考查坐标与图形的变化﹣旋转，解题的关键是掌握旋转变换的性质．‎ ‎11．为了了解某校九年级学生的体能情况，随机抽查了该校九年级若干名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的直方图，请根据图示计算，仰卧起坐次数在25～30次的学生人数占被调查学生人数的百分比为（　　）‎ A．40% B．30% C．20% D．10%‎ ‎【分析】根据频率直方图可以知道被调查的总人数，又在要求的范围可以很直观地由图形看出，即可得出百分比．‎ 解：由频率直方图可以得出，被调查的总人数＝3+10+12+5＝30．又仰卧起坐次数在25～30次的学生人数为12，故百分比为40%．‎ ‎【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．‎ ‎12．如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（　　）‎ A．（2，5） B．（5，2） C．（2，﹣5） D．（5，﹣2）‎ ‎【分析】由线段AB绕点O顺时针旋转90°得到线段A′B′可以得出△ABO≌△A′B′O′，∠AOA′＝90°，作AC⊥y轴于C，A′C′⊥x轴于C′，就可以得出△ACO≌△A′C′O，就可以得出AC＝A′C′，CO＝C′O，由A的坐标就可以求出结论．‎ 解：∵线段AB绕点O顺时针旋转90°得到线段A′B′，‎ ‎∴△ABO≌△A′B′O′，∠AOA′＝90°，‎ ‎∴AO＝A′O．‎ 作AC⊥y轴于C，A′C′⊥x轴于C′，‎ ‎∴∠ACO＝∠A′C′O＝90°．‎ ‎∵∠COC′＝90°，‎ ‎∴∠AOA′﹣∠COA′＝∠COC′﹣∠COA′，‎ ‎∴∠AOC＝∠A′OC′．‎ 在△ACO和△A′C′O中，‎ ‎，‎ ‎∴△ACO≌△A′C′O（AAS），‎ ‎∴AC＝A′C′，CO＝C′O．‎ ‎∵A（﹣2，5），‎ ‎∴AC＝2，CO＝5，‎ ‎∴A′C′＝2，OC′＝5，‎ ‎∴A′（5，2）．‎ 故选：B．‎ ‎【点评】本题考查了旋转的性质的运用，全等三角形的判定及性质的运用，等式的性质的运用，点的坐标的运用，解答时证明三角形全等是关键．‎ ‎13．为了解某班学生每天使用零花钱的情况，小敏随机调查了15名同学，结果如表：‎ 每天用零花钱（单位：元）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 人数 ‎2‎ ‎4‎ ‎5‎ ‎3‎ ‎1‎ 则这15名同学每天使用零花钱的众数和中位数分别是（　　）‎ A．3，3 B．5，2 C．3，2 D．3，5‎ ‎【分析】根据众数和中位数的定义分别进行解答即可．‎ 解：这15名同学每天使用零花钱的众数为3元，‎ 中位数为3元，‎ 故选：A．‎ ‎【点评】此题考查了众数和中位数，众数是一组数据中出现次数最多的数；中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．‎ ‎14．如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎【分析】直接利用平移中点的变化规律求解即可．‎ 解：由B点平移前后的纵坐标分别为1、2，可得B点向上平移了1个单位，‎ 由A点平移前后的横坐标分别是为2、3，可得A点向右平移了1个单位，‎ 由此得线段AB的平移的过程是：向上平移1个单位，再向右平移1个单位，‎ 所以点A、B均按此规律平移，‎ 由此可得a＝0+1＝1，b＝0+1＝1，‎ 故a+b＝2．‎ 故选：A．‎ ‎【点评】本题考查了坐标系中点、线段的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．‎ ‎15．如图，在矩形AOBC中，O为坐标原点，OA、OB分别在x轴、y轴上，点B的坐标为（0，3），∠ABO＝30°，将△ABC沿AB所在直线对折后，点C落在点D处，则点D的坐标为（　　）‎ A．（，） B．（2，） C．（，） D．（，3﹣）‎ ‎【分析】根据翻折变换的性质结合锐角三角函数关系得出对应线段长，进而得出D点坐标．‎ 解：∵四边形AOBC是矩形，∠ABO＝30°，点B的坐标为（0，3），‎ ‎∴AC＝OB＝3，∠CAB＝30°，‎ ‎∴BC＝AC•tan30°＝3×＝3，‎ ‎∵将△ABC沿AB所在直线对折后，点C落在点D处，‎ ‎∴∠BAD＝30°，AD＝3，‎ 过点D作DM⊥x轴于点M，‎ ‎∵∠CAB＝∠BAD＝30°，‎ ‎∴∠DAM＝30°，‎ ‎∴DM＝AD＝，‎ ‎∴AM＝3×cos30°＝，‎ ‎∴MO＝﹣3＝，‎ ‎∴点D的坐标为（，）．‎ 故选：A．‎ ‎【点评】此题主要考查了翻折变换以及矩形的性质和锐角三角函数关系，正确得出∠DAM＝30°是解题关键．‎ ‎16．如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'＝1，则A'D等于（　　）‎ A．2 B．3 C． D．‎ ‎【分析】由S△ABC＝9、S△A′EF＝4且AD为BC边的中线知S△A′DE＝S△A′EF＝2，S△ABD＝S△ABC＝，根据△DA′E∽△DAB知（）2＝，据此求解可得．‎ 解：如图，‎ ‎∵S△ABC＝9、S△A′EF＝4，且AD为BC边的中线，‎ ‎∴S△A′DE＝S△A′EF＝2，S△ABD＝S△ABC＝，‎ ‎∵将△ABC沿BC边上的中线AD平移得到△A'B'C'，‎ ‎∴A′E∥AB，‎ ‎∴△DA′E∽△DAB，‎ 则（）2＝，即（）2＝，‎ 解得A′D＝2或A′D＝﹣（舍），‎ 故选：A．‎ ‎【点评】本题主要平移的性质，解题的关键是熟练掌握平移变换的性质与三角形中线的性质、相似三角形的判定与性质等知识点．‎ ‎17．如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A、B、C、D不重合），经过P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为（　　）‎ A． B． C． D．‎ ‎【分析】OP的长度不变，始终等于半径，则根据矩形的性质可得OQ＝1，再由走过的角度代入弧长公式即可．‎ 解：∵PM⊥AB于点M，PN⊥CD于点N，‎ ‎∴四边形ONPM是矩形，‎ 又∵点Q为MN的中点，‎ ‎∴点Q为OP的中点，‎ 则OQ＝1，‎ 点Q走过的路径长＝＝．‎ 故选：A．‎ ‎【点评】本题考查了弧长的计算及矩形的性质，解答本题的关键是根据矩形的性质得出点Q运动轨迹的半径，要求同学们熟练掌握弧长的计算公式．‎ ‎18．如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S△PAB＝S矩形ABCD，则点P到A、B两点距离之和PA+PB的最小值为（　　）‎ A． B． C．5 D．‎ ‎【分析】首先由S△PAB＝S矩形ABCD，得出动点P在与AB平行且与AB的距离是2的直线l上，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．然后在直角三角形ABE中，由勾股定理求得BE的值，即PA+PB的最小值．‎ 解：设△ABP中AB边上的高是h．‎ ‎∵S△PAB＝S矩形ABCD，‎ ‎∴AB•h＝AB•AD，‎ ‎∴h＝AD＝2，‎ ‎∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．‎ 在Rt△ABE中，∵AB＝5，AE＝2+2＝4，‎ ‎∴BE＝＝＝，‎ 即PA+PB的最小值为．‎ 故选：D．‎ ‎【点评】本题考查了轴对称﹣最短路线问题，三角形的面积，矩形的性质，勾股定理，两点之间线段最短的性质．得出动点P所在的位置是解题的关键．‎ ‎19．如图，扇形AOB的半径为1，∠AOB＝90°，以AB为直径画半圆，则图中的阴影部分的面积为（　　）‎ A． B．π C．π D．π ‎【分析】根据阴影部分的面积＝△AOB的面积+半圆的面积﹣扇形AOB的面积和扇形的面积公式S＝计算即可．‎ 解：扇形AOB的半径为1，∠AOB＝90°，‎ ‎∴AB＝，‎ 阴影部分的面积＝×1×1+π×（）2﹣‎ ‎＝+π﹣π ‎＝‎ 故选：A．‎ ‎【点评】本题考查的是阴影面积的计算，掌握扇形的面积公式S＝是解题的关键．‎ ‎20．如图，在Rt△ACB中，∠ACB＝90°，AC＝BC，点D是AB上的一个动点（不与点A，B重合），连接CD，将CD绕点C顺时针旋转90°得到CE，连接DE，DE与AC相交于点F，连接AE，则图中与△ACE全等或相似的三角形有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【分析】先证明△ACE≌△BCD，得∠CAE＝∠CEF＝45°，再证明△ACE∽△ECF，最后证明△ACE∽△ADF，便可得结论．‎ 解：∵将CD绕点C顺时针旋转90°得到CE，‎ ‎∴CE＝CB，∠ACB＝∠DCE＝90°，‎ ‎∴∠BCD＝∠ACE，‎ 在△ACE和△BCD中，‎ ‎，‎ ‎∴△ACE≌△BCD（SAS）；‎ ‎∴∠CAE＝∠B＝∠CEF＝45°，‎ ‎∵∠ACE＝∠ECF，‎ ‎∴△ACE∽△ECF；‎ ‎∵∠FAD＝∠FEC＝45°，∠AFD＝∠EFC，‎ ‎∴∠ADF＝∠ACE，‎ ‎∵∠DAF＝∠CAE＝45°，‎ ‎∴△ACE∽△ADF，‎ 综上，图中与△ACE全等或相似的三角形有3个．‎ 故选：C．‎ ‎【点评】本题主要考查了等腰直角三角形的性质，旋转的性质，相似三角形的性质与判定，全等三角形的性质与判定，图形复杂，要善于观察，不重不漏地找出符合条件的三角形．‎ 二、填空题（本大题共5个小题．每小题4分，共20分．把答案填在答题卡的横线上.）‎ ‎21．已知一个正n边形的每个内角都为144°，则边数n为　十　．‎ ‎【分析】根据多边形的内角和公式（n﹣2）•180°列方程求解即可．‎ 解：由题意得，（n﹣2）•180°＝144°•n，‎ 解得n＝10．‎ 故答案为：十．‎ ‎【点评】本题考查了多边形的内角与外角，熟记内角和公式并列出方程是解题的关键．‎ ‎22．如图，已知路灯离地面的高度AB为4.8m，身高为1.6m的小明站在D处的影长为2m，那么此时小明离电杆AB的距离BD为　4　m．‎ ‎【分析】利用中心投影的性质可判断△CDE∽△CBA，再根据相似三角形的性质求出BC的长，然后计算BC﹣CD即可．‎ 解：∵DE∥AB，‎ ‎∴△CDE∽△CBA，‎ ‎∴＝，即＝，‎ ‎∴CB＝6，‎ ‎∴BD＝BC﹣CD＝6﹣2＝4（m）．‎ 故答案为4．‎ ‎【点评】本题考查了中心投影：中心投影的光线特点是从一点出发的投射线．物体与投影面平行时的投影是放大（即位似变换）的关系．‎ ‎23．一个不透明的口袋中共有8个白球、5个黄球、5个绿球、2个红球，这些球除颜色外都相同．从口袋中随机摸出一个球，这个球是白球的概率是　　．‎ ‎【分析】先求出袋子中球的总个数及确定白球的个数，再根据概率公式解答即可．‎ 解：袋子中球的总数为8+5+5+2＝20，而白球有8个，‎ 则从中任摸一球，恰为白球的概率为＝．‎ 故答案为：．‎ ‎【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝．‎ ‎24．如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD＝90‎ ‎°，CO＝CD，若B（1，0），则点C的坐标为　（1，1）　．‎ ‎【分析】首先利用等腰直角三角形的性质得出A点坐标，再利用位似是特殊的相似，若两个图形△ABC和△A′B′C′以原点为位似中心，相似比是k，△ABC上一点的坐标是（x，y），则在△A′B′C′中，它的对应点的坐标是（kx，ky）或（﹣kx，﹣ky），进而求出即可．‎ 解：∵∠OAB＝∠OCD＝90°，AO＝AB，CO＝CD，等腰Rt△OAB与等腰Rt△OCD是位似图形，点B的坐标为（1，0），‎ ‎∴BO＝1，则AO＝AB＝，‎ ‎∴A（，），‎ ‎∵等腰Rt△OAB与等腰Rt△OCD是位似图形，O为位似中心，相似比为1：2，‎ ‎∴点C的坐标为：（1，1）．‎ 故答案为：（1，1）．‎ ‎【点评】此题主要考查了位似变换的性质，正确理解位似与相似的关系，记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键．‎ ‎25．如图，在正方形ABCD中，E是边AD的中点．将△ABE沿直线BE翻折，点A落在点F处，联结DF，那么∠EDF的正切值是　2　．‎ ‎【分析】由折叠可得AE＝FE，∠AEB＝∠FEB，由折叠的性质以及三角形外角性质，即可得到∠AEB＝∠EDF，进而得到tan∠EDF＝tan∠AEB＝＝2．‎ 解：如图所示，由折叠可得AE＝FE，∠AEB＝∠FEB＝∠AEF，‎ ‎∵正方形ABCD中，E是AD的中点，‎ ‎∴AE＝DE＝AD＝AB，‎ ‎∴DE＝FE，‎ ‎∴∠EDF＝∠EFD，‎ 又∵∠AEF是△DEF的外角，‎ ‎∴∠AEF＝∠EDF+∠EFD，‎ ‎∴∠EDF＝∠AEF，‎ ‎∴∠AEB＝∠EDF，‎ ‎∴tan∠EDF＝tan∠AEB＝＝2．‎ 故答案为：2．‎ ‎【点评】本题主要考查了折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．‎