- 2021-11-06 发布 |
- 37.5 KB |
- 72页
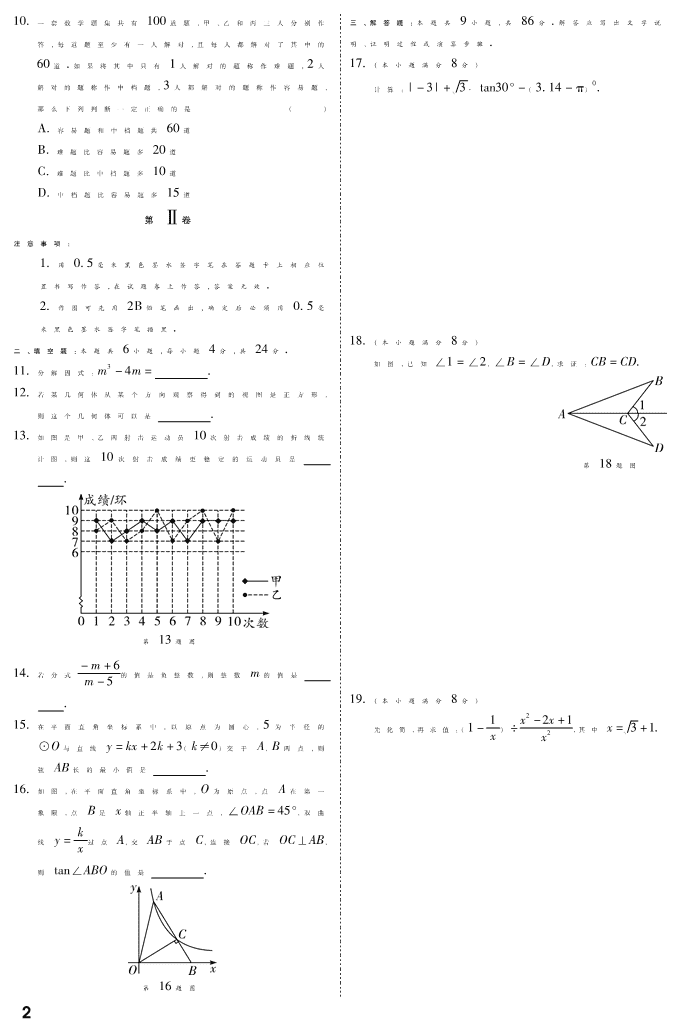

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
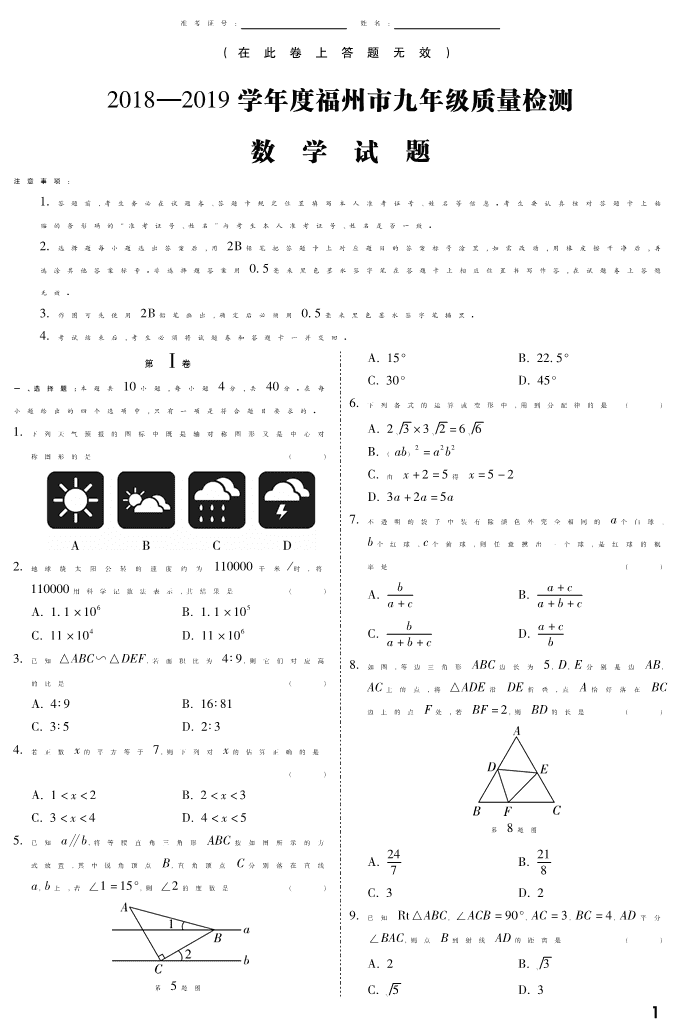
2019福建各地市数学5月质检卷及答案
书书书 准考证号: 姓名: (在此卷上答题无效) 2018—2019学年度福州市九年级质量检测 数 学 试 题 注意事项: 1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘 贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致. 2.选择题每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再 选涂其他答案标号.非选择题答案用 0.5毫米黑色墨水签字笔在答题卡上相应位置书写作答,在试题卷上答题 无效. 3.作图可先使用 2B铅笔画出,确定后必须用 0.5毫米黑色墨水签字笔描黑. 4.考试结束后,考生必须将试题卷和答题卡一并交回. 第Ⅰ卷 一、选择题:本题共 10小题,每小题 4分,共 40分.在每 小题给出的四个选项中,只有一项是符合题目要求的. 1.下列天气预报的图标中既是轴对称图形又是中心对 称图形的是 ( ) 2.地球 绕 太 阳 公 转 的 速 度 约 为 110000千 米/时,将 110000用科学记数法表示,其结果是 ( ) A.1.1×106 B.1.1×105 C.11×104 D.11×106 3.已知△ABC∽△DEF,若面积比为 4∶9,则它们对应高 的比是 ( ) A.4∶9 B.16∶81 C.3∶5 D.2∶3 4.若正数 x的平方等于 7,则下列对 x的估算正确的是 ( ) A.1<x<2 B.2<x<3 C.3<x<4 D.4<x<5 5.已知 a∥b,将等腰直角三角形 ABC按如图所示的方 式放置,其中锐角顶点 B,直角顶点 C分别落在直线 a,b上,若∠1=15°,则∠2的度数是 ( ) 第 5题图 A.15° B.22.5° C.30° D.45° 6.下列各式的运算或变形中,用到分配律的是 ( ) 槡 槡 槡A.2 3×3 2=6 6 B.(ab)2 =a2b2 C.由 x+2=5得 x=5-2 D.3a+2a=5a 7.不透明的袋子中装有除颜色外完全相同的 a个白球、 b个红球、c个黄球,则任意摸出一个球,是红球的概 率是 ( ) A. b a+c B. a+c a+b+c C. b a+b+c D.a+c b 8.如图,等边三角形 ABC边长为 5,D,E分别是边 AB, AC上的点,将△ADE沿 DE折叠,点 A恰好落在 BC 边上的点 F处,若 BF=2,则 BD的长是 ( ) 第 8题图 A.24 7 B.21 8 C.3 D.2 9.已知 Rt△ABC,∠ACB=90°,AC=3,BC=4,AD平分 ∠BAC,则点 B到射线 AD的距离是 ( ) 槡A.2 B. 3 槡 C. 5 D.3 1 10.一套数学题集共有 100道题,甲、乙和丙三人分别作 答,每道题至少有一人解对,且每人都解对了其中的 60道.如果将其中只有 1人解对的题称作难题,2人 解对的题称作中档题,3人都解对的题称作容易题, 那么下列判断一定正确的是 ( ) A.容易题和中档题共 60道 B.难题比容易题多 20道 C.难题比中档题多 10道 D.中档题比容易题多 15道 第Ⅱ卷 注意事项: 1.用 0.5毫米黑色墨水签字笔在答题卡上相应位 置书写作答,在试题卷上作答,答案无效. 2.作图可先用 2B铅笔画出,确定后必须用 0.5毫 米黑色墨水签字笔描黑. 二、填空题:本题共 6小题,每小题 4分,共 24分. 11.分解因式:m3 -4m= . 12.若某几何体从某个方向观察得到的视图是正方形, 则这个几何体可以是 . 13.如图是甲、乙两射击运动员 10次射击成绩的折线统 计图,则这 10次射击成绩更稳定的运动员是 . 第 13题图 14.若分式 -m+6 m-5的值是负整数,则整数 m的值是 . 15.在平面直角坐标系中,以原点为圆心,5为半径的 ⊙O与直线 y=kx+2k+3(k≠0)交于 A,B两点,则 弦 AB长的最小值是 . 16.如图,在平面直角坐标系中,O为原点,点 A在第一 象限,点 B是 x轴正半轴上一点,∠OAB=45°,双曲 线 y=k x过点 A,交 AB于点 C,连接 OC,若 OC⊥AB, 则 tan∠ABO的值是 . 第 16题图 三、解答题:本题共 9小题,共 86分.解答应写出文字说 明、证明过程或演算步骤. 17.(本小题满分 8分) 计算: 槡|-3|+ 3·tan30°-(3.14-π)0. 18.(本小题满分 8分) 如图,已知∠1=∠2,∠B=∠D,求证:CB=CD. 第 18题图 19.(本小题满分 8分) 先化简,再求值:(1-1 x)÷x2-2x+1 x2 ,其中 x 槡=3+1 . 2 20.(本小题满分 8分) 如图,在 Rt△ABC中,∠ACB=90°,BD平分∠ABC. 求作⊙O,使得点 O在边 AB上,且⊙O经过 B,D两 点;并证明 AC与⊙O相切.(要求尺规作图,保留作 图痕迹,不写作法) 第 20题图 21.(本小题满分 8分) 如图,将△ABC沿射线 BC平移得到△A′B′C′,使得 点 A′落在∠ABC的平分线 BD上,连接 AA′,AC′. (1)判断四边形 ABB′A′的形状,并证明; (2)在△ABC中,AB=6,BC=4,若 AC′⊥A′B′,求四 边形 ABB′A′的面积. 第 21题图 22.(本小题满分 10分) 为了解某校九年级学生体能训练情况,该年级在 3 月份进行了一次体育测试,决定对本次测试的成绩 进行抽样分析.已知九年级共有学生 480人.请按要 求回答下列问题: (1)把全年级同学的测试成绩分别写在没有明显差 别的小纸片上,揉成小球,放到一个不透明的袋子 中,充分搅拌后,随意抽取 30个,展开小球,记录这 30张纸片中所写的成绩,得到一个样本.你觉得上 面的抽取过程是简单随机抽样吗? 答: .(填“是”或“不是”) (2)下表是用简单随机抽样方法抽取的 30名同学 的体育测试成绩(单位:分): 59 69 77 73 72 62 79 78 66 81 85 84 83 84 86 87 88 85 86 89 90 97 91 98 90 95 96 93 92 99 若成绩为 x分,当 x≥90时记为 A等级,80≤x<90 时记为 B等级,70≤x<80时记为 C等级,x<70时 记为 D等级,根据表格信息,解答下列问题: ①本次抽样调查获取的样本数据的中位数是 ; 估计全年级本次体育测试成绩在 A,B两个等级的 人数是 ; ②经过一个多月的强化训练发现 D等级的同学平 均成绩提高 15分,C等级的同学平均成绩提高 10 分,B等级的同学平均成绩提高 5分,A等级的同学 平均成绩没有变化,请估计强化训练后全年级学生 的平均成绩提高多少分? 23.(本小题满分 10分) 某汽车销售公司销售某厂家的某款汽车,该款汽车 现在的售价为每辆 27万元,每月可售出两辆.市场 调查反映:在一定范围内调整价格,每辆降低 0.1万 元,每月能多卖一辆.已知该款汽车的进价为每辆 25万元.另外,月底厂家根据销售量一次性返利给 销售公司,销售量在 10辆以内(含 10辆),每辆返利 0.5万元;销售量在 10辆以上, 超过的部分每辆返 3 利 1万元.设该公司当月售出 x辆该款汽车.(总利 润 =销售利润 +返利) (1)设每辆汽车的销售利润为 y万元,求 y与 x之间 的函数关系式; (2)当 x>10时,该公司当月销售这款汽车所获得的 总利润为 20.6万元,求 x的值. 24.(本小题满分 13分) 在正方形 ABCD中,E是对角线 AC上一点(不与点 A,C重合),以 AD,AE为邻边作平行四边形 AEGD, GE交 CD于点 M,连接 CG. (1)如图①,当 AE<1 2AC时,过点 E作 EF⊥BE交 CD于点 F,连接 GF并延长交 AC于点 H. ①求证:EB=EF; ②判断 GH与 AC的位置关系,并证明; (2)过点 A作 AP⊥直线 CG于点 P,连接 BP,若 BP =10,当点 E不与 AC中点重合时,求 PA与 PC的数 量关系. 第 24题图 25.(本小题满分 13分) 已知抛物线 y=-1 2(x+5)(x-m)(m>0)与 x轴 交于点 A,B(点 A在点 B的左边),与 y轴交于点 C. (1)直接写出点 B,C的坐标;(用含 m的式子表示) (2)若抛物线与直线 y=1 2x交于点 E,F,且点 E,F 关于原点对称,求抛物线的解析式; (3)若点 P是线段 AB上一点,过点 P作 x轴的垂线 交抛物线于点 M,交直线 AC于点 N,当线段 MN长 的最大值为25 8时,求 m的取值范围 . 4 2019年厦门市初中毕业班教学质量检测数学 (试卷满分:150分 考试时间:120分钟) 一、选择题(本大题有 10小题,每小题 4分,共 40分.每 小题都有四个选项,其中有且只有一个选项正确) 1.计算(-1)3,结果正确的是 ( ) A.-3 B.-1 C.1 D.3 2.如图,在△ACB中,∠C=90°,则BC AB等于 ( ) A.sinA B.sinB C.tanA D.tanB 第 2题图 第 5题图 3.在平面直角坐标系中,若点 A在第一象限,则点 A关 于原点的中心对称点在 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.若槡n是有理数,则 n的值可以是 ( ) A.-1 B.2.5 C.8 D.9 5.如图,AD,CE是△ABC的高,过点 A作 AF∥BC,则下 列线段的长可表示图中两条平行线之间的距离的是 ( ) A.AB B.AD C.CE D.AC 6.命题:直角三角形的一条直角边与以另一条直角边为 直径的圆相切.符合该命题的图形是 ( ) 7.若方程(x-m)(x-a)=0(m≠0)的根是 x1 =x2 =m, 则下列结论正确的是 ( ) A.a=m且 a是该方程的根 B.a=0且 a是该方程的根 C.a=m但 a不是该方程的根 D.a=0但 a不是该方程的根 8.一个不透明盒子里装有 a只白球、b只黑球、c只红 球,这些球 仅 颜 色 不 同.从中 随机 摸出 一只 球,若 P(摸出白球)=1 3,则下列结论正确的是 ( ) A.a=1 B.a=3 C.a=b=c D.a=1 2(b+c) 9.已知菱形 ABCD与线段 AE,且 AE与 AB重合.现将线 段 AE绕点 A逆时针旋转 180°,在旋转过程中,若不 考虑点 E与点 B重合的情形,点 E还有三次落在菱 形 ABCD的边上,设∠B=α,则下列结论正确的是 ( ) A.0°<α<60° B.α=60° C.60°<α<90° D.90°<α<180° 10.已知二次函数 y=-3x2 +2x+1的图象经过点 A(a, y1),B(b,y2),C(c,y3),其中 a,b,c均大于 0.记点 A,B,C到该二次函数的对称轴的距离分别为 dA, dB,dC.若 dA <1 2<dB <dC,则下列结论正确的是 ( ) A.当 a≤x≤b时,y随着 x的增大而增大 B.当 a≤x≤c时,y随着 x的增大而增大 C.当 b≤x≤c时,y随着 x的增大而减小 D.当 a≤x≤c时,y随着 x的增大而减小 二、填空题(本大题有 6小题,每小题 4分,共 24分) 11.计算:-a+3a= . 12.不等式 2x-3≥0的解集是 . 第 13题图 13.如图,在平面直角坐标系中, 若ABCD的顶点 A,B,C的 坐标 分 别 是 (2,3),(1,- 1),(7,-1),则点 D的坐标 是 . 14.某服装店为调动营业员的积极性,决定实行目标管 理,根据每月销售目标完成情况发放奖金.该店统计 了每位营业员前半年的月均销售额,并算出所得数 据的平均数、众数、中位数,分别为 22,15,18(单位: 万元).若想让一半左右的营业员都能达到月销售 目标,则月销售额定为 万元较为合适. 15.在平面直角坐标系 xOy中,直线 y=x与双曲线 y=k x (k>0,x>0)交于点 A.过点 A作 AC⊥x轴于点 C,过 双曲线上另一点 B作 BD⊥x轴于点 D,作 BE⊥AC于 点 E,连接 AB.若 OD=3OC,则 tan∠ABE= . 第 16题图 16.如图,在矩形 ABCD中,AB>BC,以点 B为圆心,AB的长为半径的圆分别 交 CD边于点 M,交 BC边的延长线 于点 E.若 DM=CE, ) AE的长为 2π,则 CE的长 . 5 三、解答题(本大题有 9小题,共 86分) 17.(本题满分 8分)解方程组 x+y=4, x-2y=1{ . 18.(本题满分 8分)如图,已知点 B,C,D,E在一条直线 上,AB∥FC,AB=FC,BC=DE. 求证:AD∥FE. 第 18题图 19.(本 题 满 分 8分)化 简 并 求 值:(2a2 -4 a2 -1) ÷ a2 +2a a2 ,其中 a 槡= 2. 20.(本题满分 8分)在正方形 ABCD中,E是 CD边上的 点,过点 E作 EF⊥BD于 F. (1)尺规作图:在图中求作点 E,使得 EF=EC; (保留作图痕迹,不写作法) (2)在(1)的条件下,连接 FC,求∠BCF的度数. 第 20题图 21.(本题满分 8分)某路段上有 A,B两处相距近 200m 且未设红绿灯的斑马线.为使交通高峰期该路段车 辆与行人的通行更有序,交通部门打算在汽车平均 停留时间较长的一处斑马线上放置移动红绿灯.图 ①,图②分别是交通高峰期来往车辆在 A,B斑马线 前停留时间的抽样统计图.根据统计图解决下列 问题: 第 21题图 6 (1)若某日交通高峰期共有 350辆车经过 A斑马 线,请估计该日停留时间为 10s~12s的车辆数,以 及这些停留时间为 10s~12s的车辆的平均停留时 间;(直接写出答案) (2)移动红绿灯放置在哪一处斑马线上较为合适? 请说明理由. 22.(本题满分 10分)如图,已知△ABC及其外接圆, ∠C=90°,AC=10. (1)若该圆的半径为 槡5 2,求∠A的度数; (2)点 M在 AB边上(AM>BM),连接 CM并延长交 该圆于点 D,连接 DB,过点 C作 CE垂直 DB的延长 线于 E.若 BE=3,CE=4,试判断 AB与 CD是否互 相垂直,并说明理由. 23.(本题 满 分 10分)在 四 边 形 ABCD中,AB∥ CD, ∠ABC=60°,AB=BC=4,CD=3. (1)如图①,求△BCD的面积; (2)如图②,M是 CD边上一点,将线段 BM绕点 B 逆时针旋转 60°,可得线段 BN,过点 N作 NQ⊥BC, 垂足为 Q,设 NQ=n,BQ=m,求 n关于 m的函数解 析式.(自变量 m的取值范围只需直接写出) 第 23题图 24.(本题满分 12分)某村启动“脱贫攻坚”项目,根据 当地的地理条件,要在一座高为 1000m的山上种植 一种经济作物.农业技术人员在种植前进行了主要 相关因素的调查统计,结果如下: ①这座山的山脚下温度约为22℃,山高 h(单位:m)每 增加 100m,温度 T(单位:℃)下降约 0.5℃; ②该作物的种植成活率 p受温度 T影响,且在 19℃ 时达到最大.大致如表一: 表一 温度 T℃ 21 20.5 20 19.5 19 18.5 18 17.5 种植成 活率 p 90% 92% 94% 96% 98% 96% 94% 92 % 7 ③该作物在这座山上的种植量 w受山高 h影响,大 致如图: 第 24题图 (1)求 T关于 h的函数解析式,并求 T的最小值; (2)若要求该作物种植成活率 p不低于 92%,根据 上述统计结果,山高 h为多少米时该作物的成活量 最大?请说明理由. 25.(本题满分 14分)在平面直角坐标系 xOy中,已知点 A,对点 A作如下变换: 第一步:作点 A关于 x轴的对称点 A1;第二步:以 O 为位似中心,作线段 OA1 的位似图形 OA2,且相似比 OA2 OA1 =q,则称 A2 是点 A的对称位似点. (1)若 A(2,3),q=2,直接写出点 A的对称位似点的 坐标; (2)已知直线 l:y=kx-2,抛物线 C:y=-1 2x2 +mx -2(m>0).点 N(m(m-k) k2 ,2k-2)在直线 l上. ①当 k=1 2时,判断 E(1,-1)是否是点 N的对称位 似点,请说明理由; ②若直线 l与抛物线 C交于点 M(x1,y1)(x1≠0),且 点 M不是抛物线的顶点,则点 M的对称位似点是否 可能仍在抛物线 C上?请说明理由 . 8 2019年福建省泉州市初中学业质量检查 数学试卷 (满分:150分;考试时间:120分钟) 第Ⅰ卷 一、选择题:本大题共 10小题,每小题 4分,共 40分.在每 小题给出的四个选项中,只有一项是符合题目要求的. 1.在 -1,2,1 3,槡3这四个数中,无理数是 ( ) A.-1 B.2 C.1 3 D.槡3 2.下列运算结果为 a3 的是 ( ) A.a+a+a B.a5 -a2 C.a·a·a D.a6 ÷a2 3.一个几何体的三视图如图所示,则这个几何体是 ( ) 4.人 体 中 红 细 胞 的 直 径 约 为 0.0000077m,将 数 字 0.0000077用科学记数法表示为 ( ) A.7.7×10-5 B.0.77×10-5 C.7.7×10-6 D.77×10-7 5.下列事件中,是必然事件的是 ( ) A.从装有 10个黑球的不透明袋子中摸出一个球,恰 好是红球 B.抛掷一枚普通正方体骰子所得的点数小于 7 C.抛掷一枚普通硬币,正面朝上 D.从一副没有大小王的扑克牌中抽出一张牌,恰好 是方块 6.小王和小丽下棋,小王执圆子,小丽执方子.如图是在 直角坐标系中棋子摆出的图案,若再摆放一圆一方两 第 6题图 枚棋子,使 9枚棋子组成的图案 既是轴对称图形又是中心对称 图形,则这两枚棋子的坐标分别 是 ( ) A.圆子(2,3),方子(1,3) B.圆子(1,3),方子(2,3) C.圆子(2,3),方子(4,0) D.圆子(4,0),方子(2,3) 7.关于 x的一元二次方程 x2 -mx-1=0的根的情况是 ( ) A.有两个不相等的实数根 B.有两个相等的实数根 C.无实数根 D.不能确定 8.一次函数 y=-2x+1的图象不经过 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 9.如图,抛物线 y=ax2 +bx+c(a>0)过原点 O,与 x轴 另一交点为 A,顶点为 B,若△AOB为等边三角形,则 b的值为 ( ) A. 槡- 3 B. 槡-2 3 C. 槡-3 3 D. 槡-4 3 第 9题图 第 10题图 10.如图,点 E为△ABC的内心,过点 E作 MN∥BC交 AB于点 M,交 AC于点 N,若 AB=7,AC=5,BC=6, 则 MN的长为 ( ) A.3.5 B.4 C.5 D.5.5 第Ⅱ卷 二、填空题:本大题共 6小题,每小题 4分,共 24分. 11.计算:(1 2)-1 +(槡3-1)0 = . 12.若一组数据 1,3,x,5,8的众数为 8,则这组数据的中 位数为 . 13.在五边形 ABCDE中,若 ∠A+∠B+∠C+∠D= 440°,则∠E= °. 14.若 x=a, y={ b 是 方 程 组 2x-y=1, -x+5y{ =5 的 解,则 a+4b = . 第 15题图 15.如图,PA切⊙O于点 A,点 B是 线段 PO的中点,若⊙O的半径 为槡3,则图中阴影部分的面积 为 . 16.在平面直角坐标系中,点 A的 坐标为(4,0),点 B为 y轴上的一动点,将线段 AB 绕点 B顺时针旋转 90°得线段 BC,若点 C恰好落在 反比 例 函 数 y= 3 x的 图 象 上,则 点 B的 坐 标 为 . 9 三、解答题:本大题共 9小题,共 86分,解答应写出文字 说明,证明过程或演算步骤. 17.(8分)解不等式组 x+4≥2, 2x>-3+3x{ , 并将解集在数轴 上表示出来. 第 17题图 18.(8分)先化简,再求值:(a+ 1 a-2)÷a2 -1 a2 +a,其中 a =-2. 19.(8分)如图,在△ABC中,AB=AC,CD⊥AB于点 D, BE⊥AC于点 E. 第 19题图 求证:BD=CE. 20.(8分)《杨辉算法》中有这么一道题:“直田积八百 六十四步,只云长阔共六十步,问长多阔几何?”意 思是:一块矩形田地的面积为 864平方步,只知道它 的长与宽共 60步,问它的长比宽多了多少步? 21.(8分)如图,在ABCD中,AC与 BD相交于点 O, AC⊥BC,垂足为 C,将△ABC沿 AC翻折得到△AEC, 连接 DE. (1)求证:四边形 ACED是矩形; (2)若 AC=4,BC=3,求 sin∠ABD的值. 第 21题图 22.(10分)电器专营店的经营利润受地理位置、顾客消 费能力等因素的影响.某品牌电脑专营店设有甲、乙 两家分店,均销售 A、B、C、D四种款式的电脑,每种 款式电脑的利润如表 1所示.现从甲、乙两店每月售 出的电脑中各随机抽取所记录的 50台电脑的款式, 统计各种款式电脑的销售数量,如表 2所示. 表 1:四种款式电脑的利润 电脑款式 A B C D 利润(元 /台) 160 200 240 320 表 2:甲、乙两店电脑销售情况 电脑款式 A B C D 甲店销售数量(台) 20 15 10 5 乙店销售数量(台) 8 10 14 18 试运用统计与概率知识,解决下列问题: (1)从甲店每月售出的电脑中随机抽取一台,其利 润不少于 240元的概率为 ; (2)经市场调查发现,甲、乙两店每月电脑的总销量 相当.现由于资金限制,需对其中一家分店作出暂停 营业的决定,若从每台电脑的平均利润的角度考虑, 你认为应对哪家分店作出暂停营业的决定?并说明 理由 . 01 23.(10分)在平面直角坐标系中,反比例函数 y=k x(k >0,x>0)图象上有两点(n,3n)、(n+1,2n). (1)求 n的值; (2)如图,直线 l为正比例函数 y=x的图象,点 A在 反比例函数 y= k x(k>0,x>0)图象上,过点 A作 AB⊥l于点 B,过点 B作 BC⊥x轴于点 C,过点 A作 AD⊥BC于点 D,记△BOC的面积为 S1,△ABD的面 积为 S2,求 S1 -S2 的值. 第 23题图 24.(13分)如图,在菱形 ABCD中,点 E是 BC边上一动 点(不与点 C重合),对角线 AC与 BD相交于点 O, 连接 AE,交 BD于点 G. (1)根据给出的△AEC,作出它的外接圆⊙F,并标 出圆心 F(不写作法和证明,保留作图痕迹); (2)在(1)的条件下,连接 EF. ①求证:∠AEF=∠DBC; ②记 t=GF2 +AG·GE,当 AB=6,BD 槡=6 3时,求 t 的取值范围. 第 24题图 25.(13分)如图,二次函数 y=x2 +bx-3的图象与 x轴 分别相交于 A,B两点,点 B的坐标为(3,0),与 y轴 的交点为 C,动点 T在射线 AB上运动,在抛物线的 对称轴 l上有一定点 D,其纵坐标为 槡2 3,l与 x轴的 交点为 E,经过 A,T,D三点作⊙M. (1)求二次函数的表达式; (2)在点 T的运动过程中, ①∠DMT是否为定值?若是,请求出该定值;若不 是,请说明理由; ②若 MT=1 2AD,求点 M的坐标; (3)当动点 T在射线 EB上运动时,过点 M作MH⊥x 轴于点 H,设 HT=a,当 OH≤x≤OT时,求 y的最大 值与最小值(用含 a的式子表示). 第 25题图 11 2019年漳州市初中毕业班质量检测数学试卷 (满分:150分;考试时间:120分钟) 一、选择题(本大题共 10小题,每小题 4分,共 40分.在 每小题给出的四个选项中,只有一项是符合题目要求 的,请在答题卡的相应位置填涂) 1.-3的倒数是 A.3 B.-3 C.1 3 D.-1 3 2.在百度搜索引擎中,输入“魅力漳州”四个字,百度为 您找到相关结果约 1600000个,数据 1600000用科学 记数法表示,正确的是 A.16×105 B.1.6×106 C.1.6×107 D.0.16×108 3.下面四大手机品牌图标中,轴对称图形的是 4.在圆锥、圆柱、球、正方体这四个几何体中,主视图不 可能是多边形的是 A.圆锥 B.圆柱 C.球 D.正方体 5.如图,AB∥CD∥EF,AC=4,CE=6,BD=3,则 DF的 值是 A.4.5 B.5 C.5.5 D.1.5 第 5题图 第 6题图 6.实数 a,b,c在数轴上的对应点的位置如图所示,如果 a+b=0,那么下列结论错误的是 A.|a|=|b| B.a+c>0 C.a b=-1 D.abc>0 7.如图,向正六边形的飞镖游戏盘内随机投掷一枚飞 镖,则该飞镖落在阴影部分的概率是 第 7题图 A.1 2 B.1 3 C.1 4 D.2 3 8.下列函数中,对于任意实数 x,y随 x的增大而减小 的是 A.y=1 2x B.y=2 x C.y=-x+2 D.y=2x2 9.若 x=2是关于 x的一元一次方程 ax-2=b的解,则 3b-6a+2的值是 A.-8 B.-4 C.8 D.4 10.如图,正方形 ABCD中,对角线 AC、BD相交于点 O, 点 E是 BC的中点,AE交 BD于点 F,BH⊥AE于点 G,连接 OG,则下列结论中: 第 10题图 ①OF=OH;②△AOF∽△BGF;③ tan∠GOH=2;④FG+GH 槡= 2GO. 正确的个数是 A.1 B.2 C.3 D.4 二、填空题(本大题共 6小题,每小题 4分,共 24分.请将 答案填入答题卡的相应位置) 11.计算:槡( )3-10 = . 12.若直角三角形两直角边长为 6和 8,则此直角三角形 斜边上的中线长是 . 13.若一组数据 1,2,3,x的平均数是 2,则这组数据的 方差是 . 14.如 图,⊙O 是 △ABC 的 外 接 圆,∠A=45°,则 cos∠OCB的值是 . 第 14题图 第 16题图 15.若 x1,x2 是一元二次方程 ax2 +bx+c=0(a≠0)的两 根,则 x1 +x2 =-b a,x1x2 = c a;已知 m,n是方程 x2 +2x-1=0的两个根,则 m2n+mn2 = . 16.如图,矩形 OABC的边 OA,OC分别在 x轴、y轴上, 点 B的坐标为(8,4),反比例函数 y=k x(k>0)的图 象分别交边 BC,AB于点 D,E,连接 DE,△DEF与 △DEB关于直线 DE对称.当点 F恰好落在线段 OA 上时,则 k的值是 . 21 三、解答题(本大题共 9小题,共 86分.请在答题卡的相 应位置解答) 17. (本 小 题 满 分 8 分 ) 解 不 等 式 组: 1-x≤ -2, 3(x-1)<x+5{ , 并把解集在数轴上表示出来. 18.(本小题满分 8分)先化简,再求值:(a2 +b2 a -2b)÷ a2 -b2 a ,其中 a 槡= 2-1,b=1. 19.(本小题满分 8分)求证:等腰三角形两底角的角平 分线相等. (要求:画出图形,写出已知、求证,并给予证明) 20.(本小题满分 8分)我国古代《算法统宗》里有这样 一首诗:我问开店李三公,众客都来到店中,一房七 客多七客,一房九客一房空.诗中后两句的意思是: 如果每一间客房住 7人,那么有 7人无房可住;如果 每一间客房住 9人,那么就空出一间房.求该店有客 房多少间?房客多少人? 21.(本小题满分 8分)某校兴趣小组就“最想去的漳州 5个最美乡村”随机调查了本校部分学生,要求每位 同学选择且只能选择一个最想去的最美乡村.下面 是根据调查结果绘制出的尚不完整统计表和统计 图,其中 x、y是满足 x<y的正整数. 最美乡村意向统计表 最美乡村 人数 A:龙海埭美村 10 B:华安官畲村 11 C:长泰山重村 4x D:南靖塔下村 9 E:东山澳角村 3y 最美乡村意向扇形统计图 第 21题图 根据以上信息,解答下列问题 (1)求 x、y的值; (2)若该校有 1200名学生,请估计“最想去华安官 畲村”的学生人数. 22.(本小题满分 10分)如图,在△ABC中,AB 槡= 3,AC 槡= 6,BC=3,将△ABC沿射线 BC平移,使边 AB平 移到 DE,得到△DEF. (1)作出平移后的△DEF(要求:尺规作图,保留作 图痕迹,不写作法); (2)若 AC、DE相交于点 H,BE=2,求四边形 DHCF 的面积. 第 22题图 31 23.(本小题满分 10分)如图,AB是⊙O的直径,AC为 ⊙O的弦,OD⊥AB,OD与 AC的延长线交于点 D,点 E在 OD上,且∠ECD=∠B. (1)求证:EC是⊙O的切线; (2)若 OA=3,AC=2,求线段 CD的长. 第 23题图 24.(本小题满分 12分)已知,如图①,在平行四边形 ABCD中,AB=6,∠B=α(60°<α≤90°),点 E在 BC 上,连接 AE,把△ABE沿 AE折叠,使点 B与 AD上 的点 F重合,连接 EF. (1)求证:四边形 ABEF是菱形; (2)如图②,点 M是 BC上的动点,连接 AM,把线段 AM绕点 M顺时针旋转 α得线段 MN,连接 FN,求 FN的最小值(用含 α的代数式表示). 第 24题图 25.(本小题满分 14分)已知,抛物线 y=x2 +(2m-1)x -2m(-1 2<m≤ 3 2),直线 l的解析式为 y=(k- 1)x+2m-k+2. (1)若抛物线与 y轴交点的纵坐标为 -3,试求抛物 线的顶点坐标; (2)试证明:抛物线与直线 l必有两个交点; (3)若抛物线经过点(x0,-4),且对于任意实数 x, 不等式 x2 +(2m-1)x-2m≥ -4都成立;当k-2≤ x≤k时,抛物线的最小值为 2k+1,求直线 l的解 析式 . 41 2019年莆田市初中毕业班质量检查试卷数学 (满分:150分;考试时间:120分钟) 一、选择题:本大题共 10小题,每小题 4分,共 40分.在 每小题 给 出 的 四 个 选 项 中,只 有 一 项 是 符 合 题 目 要 求的. 1.下列四个数中,最大的数是 A.-2 B.-1 C.0 D.|-3| 2.下列几何体中,俯视图为三角形的是 3.下列式子中,可以表示为 2-3的是 A.22 ÷25 B.25 ÷22 C.22 ×25 D.(-2)×(-2)×(-2) 4.将一把直尺和一块含 30°的直角三角板 ABC按如图所 示的位置放置,若∠CDE=40°,则∠BAF的大小为 第 4题图 A.10° B.15° C.20° D.25° 5.若 4<k<5,则 k的可能值是 A. 3槡 2 槡 槡B.8 C.2 3 D.槡 槡4+ 5 6.点 E(m,n)在平面直角坐标系中的位置如图所示,则 第 6题图 坐标 (m+1,n-1)对应的点可 能是 A.A点 B.B点 C.C点 D.D点 7.某排球队 6名场上队员的身高(单位:cm)是:180, 184,188,190,192,194.现用一名身高为 186cm的队 员换下场上身高为 192cm的队员,与换人前相比,场 上队员的身高 A.平均数变小,中位数变小 B.平均数变小,中位数变大 C.平均数变大,中位数变小 D.平均数变大,中位数变大 8.下列直线与过(-2,0),(0,3)的直线的交点在第一象 限的是 A.x=-3 B.x=3 C.y=-3 D.y=3 9.如图,AB,AC均为⊙O的切线,切点分别为 B,C,点 D 在优弧 ) BC上.则下列关系式中一定成立的是 A.∠A+∠D=180° B.∠A+2∠D=180° C.∠B+∠C=270° D.∠B+2∠C=270° 第 9题图 第 10题图 10.加工爆米花时,爆开且不糊的粒数占加工总粒数的 百分比称为“可食用率”.在特定条件下,可食用率 p 与加工时间 t(单位:分钟)满足的函数关系为 p=at2 +bt+c(a,b,c是常数),如图记录了三次实验的数 据.根据上述函数模型和实验数据,可得到最佳加工 时间为 A.4.25分钟 B.4.00分钟 C.3.75分钟 D.3.50分钟 二、填空题:本大题共 6小题,每小题 4分,共 24分. 11.莆田市政府推出“YouBike微笑自行车”的社会公共 服务项目,旨在发展全民健身,打造健康莆田.预计 2019年年底将建设 970个公共自行车租赁站点,投 入自行车 31000辆.将 31000写成科学记数法为 . 12.方程组 x-y=2, 2x+y{ =4 的解是 . 第 13题图 13.如图,△ABC中,AB+AC=6, BC的垂直平分线 DE交 AB 于 点 D,交 BC 于 点 E,则 △ACD的周长为 . 14.在一个不透明的袋子里,有 2 个黑球和 1个白球,除了颜色外全部相同,任意摸出 两个球,这两个球中有白球的概率是 . 15.尺规作图特有的魅力使无数人沉湎其中.传说拿破 仑曾通过下列尺规作图将圆等分: ①将半径为 r的⊙O六等分,依次得到 A,B,C,D,E, F六个分点 ; 51 ②分别以点 A,D为圆心,AC长为半径画弧,两弧相 交于点 G; ③连接 OG,以 OG长为半径,从点 A开始,在圆周上 依次截取,刚好将圆等分.顺次连接这些等分点构成 的多边形面积为 . 第 15题图 第 16题图 16.如图,点 P为函数 y=2 x(x>0)上一点,过点 P作 x 轴、y轴的平行线,分别与函数 y=10 x(x>0)的图象 交于点 A,B,则△AOB的面积为 . 三、解答题:本大题共 9小题,共 86分.解答应写出必要 的文字说明、证明过程、正确作图或演算步骤. 17.(本小题满分 8分)计算:π0 -3 槡8+cos60°. 18.(本小题满分 8分)求证:角的平分线上的点到角的 两边的距离相等. 19.(本小题满分 8分)化简求值:(1-2m m +1)÷1-m2 m , 其中 m=2. 20.(本小题满分 8分)如图,△ABC中,AB=AC,∠A= 80°,点 D,E分别在边 AB,AC上,且 DA=DE=CE. (1)求作点 F,使得四边形 BDEF为平行四边形;(要 求:尺规作图,保留痕迹,不写作法) (2)连接 CF,写出图中经过旋转可完全重合的两个 三角形,并指出旋转中心和旋转角. 第 20题图 21.(本小题满分 8分)我市“木兰溪左岸绿道”工程已全 部建成并投入使用,10公里的河堤便道铺满了彩色 的透水沥青,堤岸旁的各类花草争奇斗艳,与木兰溪 河滩上的特色花草相映成趣,吸引着众多市民在此 休闲锻炼、散步观光.某小区随机调查了部分居民在 一周内前往“木兰溪左岸绿道”锻炼的次数,并制成 如图不完整的统计图表. 居民前往“木兰溪左岸绿道”锻炼的次数统计表 锻炼次数 0次 1次 2次 3次 4次及以上 人数 7 13 a 10 3 居民前往“木兰溪左岸绿道”锻炼的次数统计图 第 21题图 请你根据统计图表中的信息,解答下列问题: (1)a= ,b= ; (2)请计算扇形统计图中“3次”所对应扇形的圆心 角的度数; (3)若该小区共有 2000名居民,根据调查结果,估计 该小区居民在一周内前往“木兰溪左岸绿道”锻炼“4 次及以上”的人数. 22.(本小题满分 10分)如图,在⊙O中,弦 AC⊥BD于点 E,连接 AB,CD,BC. (1)求证:∠AOB+∠COD=180°; (2)若 AB=8,CD=6,求⊙O的直径 . 61 第 22题图 23.(本小题满分 10分)直觉的误差:有一张 8cm×8cm 的正方形纸片,面积是 64cm2.把这些纸片按图①所 示剪开成四小块,其中两块是三角形,另外两块是梯 形.把剪出的 4个小块按图②所示重新拼合,这样就 得到了一个 13cm×5cm的长方形,面积是 65cm2, 面积多了 1cm2.这是为什么? 小明给出如下证明:如图②可知,tan∠CEF=8 3,tan ∠EAB=13 5, ∵tan∠CEF>tan∠EAB,∴∠CEF>∠EAB, ∵EF∥ AB,∴ ∠EAB+∠AEF=180°,∴ ∠CEF+ ∠AEF>180°, 因此 A、E、C三点不共线. 同理 A、G、C三点不共线,所以拼合的长方形内部有 空隙,故面积多了 1cm2. (1)小红给出的证明思路为:以 B为原点,BC所在的 直线为 x轴,建立平面直角坐标系,证明三点不共 线.请你帮小红完成她的证明; (2)将 13cm×13cm的正方形做类似的剪开拼合, 是否可以拼合成一个长方形,但面积少了1cm2?如 果能,求出剪开的三角形的短边长;如果不能,请说 明理由. 第 23题图 24.(本小题满分 12分)如图①,在 Rt△ABC中,∠ABC =90°,AB=BC,将△ABC绕点 A逆时针旋转,得到 △ADE,旋转角为 α(0°<α<90°),连接 BD交 CE于 点 F. (1)如图②,当 α=45°时,求证:CF=EF; (2)在旋转过程中,问(1)中的结论是否仍然成立? 证明你的结论; (3)连接 CD,当△CDF为等腰直角三角形时,求 tan α 2的值. 第 24题图 25.(本小题满分 14分)函数 y1 =kx2 +ax+a的图象与 x 轴交于点 A,B(点 A在点 B的左侧),函数 y2 =kx2 + bx+b的图象与 x轴交于点 C,D(点 C在点 D的左 侧),其中 k≠0,a≠b. (1)求证:函数 y1与 y2 的图象交点落在一条定直 线上; (2)若 AB=CD,求 a,b和 k应满足的关系式; (3)是否存在函数 y1和 y2,使得 B,C为线段 AD的三 等分点?若存在,求 a b的值;若不存在,说明理由 . 71 2019年宁德市初中毕业班质量检测 数 学 试 题 (满分 150分 考试时间:120分钟) 注意事项: 1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的 条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致. 2.选择题每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂 其他答案标号.非选择题答案用 0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效. 3.作图可先使用 2B铅笔画出,确定后必须用 0.5毫米黑色签字笔描黑. 4.考试结束,考生必须将试题卷和答题卡一并上交. 第 Ⅰ 卷 一、选择题:本题共 10小题,每小题 4分,共 40分.在每 小题给出的四个选项中,只有一项是符合题目要求的. 1.2019的绝对值是 ( ) A. 1 2019 B.2019 C.- 1 2019 D.-2019 2.下列几何体中,主视图与俯视图相同的是 ( ) 3.下列运算正确的是 ( ) A.a3·a2 =a6 B.a6 ÷a2 =a3 C.(槡2)0 =0 D.3-2 =1 9 4.若三角形的三边长分别为 3,x,5,则 x的值可以是 ( ) A.2 B.5 C.8 D.11 5.如图,在 4×4的正方形网格中,点 A,B,M,N都在格 点上.从点 M,N中任取一点,与点 A,B顺次连接组成 一个三角形,则下列事件是必然事件的是 ( ) 第 5题图 A.所得三角形是锐角三角形 B.所得三角形是直角三角形 C.所得三角形是钝角三角形 D.所得三角形是等腰三角形 6.一元二次方程 x2 -2x-1=0根的情况是 ( ) A.只有一个实数根 B.有两个相等的实数根 C.有两个不相等的实数根 D.没有实数根 7.我国古代数学名著《九章算术》有“米谷粒分”题:粮 仓开仓收粮,有人送来谷米 1534石,验得其中夹有谷 粒.现从中抽取谷米一把,共数得 254粒,其中夹有谷 粒 28粒,则这批谷米内夹有谷粒约是 ( ) A.134石 B.169石 C.338石 D.1365石 8.小卖部从批发市场购进一批杨梅,在销售了部分杨梅 之后,余下的每千克降价 3元,直至全部售完.销售金 额 y元与杨梅销售量 x千克之间的关系如图所示.若 销售这批杨梅一共赢利 220元,那么这批杨梅的进价 是 ( ) 第 8题图 A.10元/千克 B.12元 /千克 C.12.5元/千克 D.14.4元/千克 9.如图,AB是⊙O的直径,AB=AC,AC交⊙O于点 E, BC交⊙O于点 D,F是 CE的中点,连接 DF.则下列 结论错误的是 ( ) 第 9题图 A.∠A=∠ABE B. ) BD= ) DE C.BD=DC D.DF是⊙O 的切线 81 10.点 A(2,m),B(2,m-5)在平面直角坐标系中,点 O 为坐标原点.若△ABO是直角三角形,则 m的值不 可能是 ( ) A.4 B.2 C.1 D.0 第 Ⅱ 卷 注意事项: 1.用 0.5毫米黑色签字笔在答题卡上相应位置书写作 答,在试题卷上作答,答案无效. 2.作图可先使用 2B铅笔画出,确定后必须用 0.5毫米 黑色签字笔描黑. 二、填空题:本题共 6小题,每小题 4分,共 24分. 11.2018年国庆假期宁德市接待游客 2940000人次.将 数据 2940000用科学记数法表示为 . 12.如图,DA⊥CE于点 A,CD∥AB,∠1=30°,则∠D= °. 第 12题图 第 14题图 13.学校组织户外研学活动,安排给九年级三辆车,小明 与小慧都可以从三辆车中任选一辆搭乘,则小明和 小慧搭乘同一辆车的概率是 . 14.关于 x的一元一次不等式组 2-x>1, x+5 2 ≤{ m中两个不等 式的解集在同一数轴上的表示如图所示,则该不等 式组解集是 . 15.小宇计算分式的过程如图所示,他开始出现计算错 误的是在第 步.(填序号) 第 15题图 第 16题图 16.如图,已知正方形 ABCD中,点 E 是 BC上的一个动点,EF⊥AE交 CD于点 F,以 AE,EF为边作矩形 AEFG,若 AB=4,则点 G到 AD距 离的最大值是 . 三、解答题:本题共 9小题,共 86分. 17.(本题满分 8分)先化简,再求值:(x-3)2 +x(2+ x)-9,其中 x 槡=- 3. 18.(本题满分 8分)如图,F,C是 AD上两点,且 AF= CD,点 E,F,G在同一直线上,且 F,G分别是 AC,AB 中点,BC=EF. 求证:△ABC≌△DEF. 第 18题图 19.(本题满分 8分)春晓中学为开展“校园科技节”活 动,计划购买 A型、B型两种型号的航模.若购买 8 个 A型航模和 5个 B型航模需用 2200元;若购买 4 个 A型航模和 6个 B型航模需用 1520元.求 A,B两 种型号航模的单价分别是多少元 . 91 20.(本题满分 8分)某校九年级共有 80名同学参与数 学科托底训练.其中(1)班 30人,(2)班 25人,(3) 班 25人,吕老师在托底训练后对这些同学进行测 试,并对测试成绩进行整理,得到下面统计图表. 九年级托底成绩统计表 班级 平均数 中位数 众数 (1)班 75.2 m 82 (2)班 71.2 68 79 (3)班 72.8 75 75 (1)班成绩分布直方图 第 20题图 (1)表格中的 m落在 组;(填序号) ①40≤x<50, ②50≤x<60, ③60≤x<70, ④70≤x<80, ⑤80≤x<90, ⑥90≤x≤100. (2)求这 80名同学的平均成绩; (3)在本次测试中,(2)班小颖同学的成绩是 70分, (3)班小榕同学的成绩是 74分,这两位同学成绩在 自己所在班级托底同学中的排名谁更靠前?请简要 说明理由. 21.(本题满分 8分)如图,点 O是菱形 ABCD对角线的 交点,点 E在 BO上,EF垂直平分 AB,垂足为 F. (1)求证:△BEF∽△DCO; (2)若 AB=10,AC=12,求线段 EF的长. 第 21题图 22.(本题满分 8分)已知反比例函数图象上两点 A(2,3), B(-2x+2,y1)的位置如图所示. (1)求 x的取值范围; (2)若点 C(-x,y2)也在该反比例函数的图象上,试 比较 y1,y2 的大小. 第 22题图 02 23.(本题满分 12分)定义:平面内,如果一个四边形的 四个顶点到某一点的距离都相等,则称这一点为该 四边形的外心. (1)下列四边形:平行四边形、矩形、菱形中,一定有 外心的是 ; (2)已知四边形 ABCD有外心 O,且 A,B,C三点的 位置如图①所示,请用尺规确定该四边形的外心,并 画出一个满足条件的四边形 ABCD; (3)如图②,已知四边形 ABCD有外心 O,且 BC=8, sin∠BDC=4 5,求 OC的长. 第 23题图 24.(本题满分 13分)如图,在矩形 ABCD中,AB=4,AD =6,E是 AD边上的一个动点,将四边形 BCDE沿直 线 BE折叠,得到四边形 BC′D′E,连接 AC′,AD′. (1)若直线 DA交 BC′于点 F,求证:EF=BF; (2)当 AE=4 3槡3时,求证:△AC′D′是等腰三角形; (3)在 点 E的 运 动 过 程 中,求 △AC′D′面 积 的 最 小值. 第 24题图 12 25.(本题满分 13分)如图①,已知水龙头喷水的初始速 度 v0可以分解为横向初始速度 vx和纵向初始速度 vy,θ是水龙头的仰角,且 v0 2 =vx 2 +vy 2.图②是一个 建在斜坡上的花圃场地的截面示意图,水龙头的喷 射点 A在山坡的坡顶上(喷射点离地面高度忽略不 计),坡顶的铅直高度 OA为 15米,山坡的坡比为 1 3.离开水龙头后的水(看成点)获得初始速度 v0 米/秒后的运动路径可以看作是抛物线,点 M是运 动过程中的某一位置.忽略空气阻力,实验表明:M 与 A的高度之差 d(米)与喷出时间 t(秒)的关系为 d=vyt-5t2;M与 A的水平距离为 vxt米.已知该水 流的 初 始 速 度 v0 为 15米 /秒,水 龙 头 的 仰 角 θ 为 53°. (1)求水流的横向初始速度 vx和纵向初始速度 vy; (2)用含 t的代数式表示点 M的横坐标 x和纵坐标 y,并求 y与 x的关系式(不写 x的取值范围); (3)水流在山坡上的落点 C离喷射点 A的水平距离 是多少米?若要使水流恰好喷射到坡脚 B处的小 树,在相同仰角下,则需要把喷射点 A沿坡面 AB方 向移动多少米? (参考数据:sin53°≈ 4 5,cos53°≈ 3 5,tan53°≈ 4 3) 第 25题图 22 2019年龙岩市九年级学业(升学)质量检查数学试题 (满分:150分 考试时间:120分钟) 一、选择题:本大题共 10小题,每小题 4分,共 40分.每 小题的四个选项中,只有一项符合题目要求. 1.如图,数轴上的单位长度为 1,若实数 a,b所表示的数 恰好在整数点上,则 a+b= ( ) A.0 B.-1 C.1 D.5 第 1题图 2.下列所给的汽车标志图案中,既是轴对称图形,又是 中心对称图形的是 ( ) 3.下列调查中,适合采用全面调查(普查)方式的是 ( ) A.对汀江流域水质情况的调查 B.对端午节期间市场上粽子质量情况的调查 C.对某班 40名同学身高情况的调查 D.对某类烟花爆竹燃放安全情况的调查 4.若 x=a y={ b ,是方程组 2x+y=3 3x-2y{ =7 ,的解,则 5a-b的值 是 ( ) A.10 B.-10 C.14 D.21 5.下列图形中,∠1一定大于∠2的是 ( ) 6.若关于 x的一元一次不等式组 2x-1>3(x-2), x<{ m 的解 集是 x<5,则 m的取值范围是 ( ) A.m≥5 B.m>5 C.m≤5 D.m<5 7.如图,x,y,z分别表示以直角三角形三边为边长的正 方形面积,则下列结论正确的是 ( ) A.x2 =y2 +z2 B.x<y+z C.x-y>z D.x=y+z 第 7题图 第 8题图 8.三个等边三角形的摆放位置如图,若∠3=60°,则∠1 +∠2的度数为 ( ) A.90° B.120° C.270° D.360° 第 9题图 9.如图,抛物线 y=ax2 +bx+c与 x轴交于点 A(-1,0),顶点坐 标是(1,n),与 y轴的交点在 (0,3)和 (0,6)之间 (包 含端 点),则下列结论错误的是 ( ) A.3a+b<0 B.-2≤a≤ -1 C.abc>0 D.9a+3b+2c>0 10.某些整数的所有正约数之和可以按如下方法求得, 如:6=2×3,则 6的所有正约数之和为(1+3)+(2 +6)=(1+2)×(1+3)=12;12=22 ×3,则 12的 所有正约数之和为(1+3)+(2+6)+(4+12)=(1 +2+22)×(1+3)=28;36=22 ×32,则 36的所有 正约数之和为(1+3+9)+(2+6+18)+(4+12+ 36)=(1+2+22)×(1+3+32)=91,参照上述方 法,那么 144的所有正约数之和为 ( ) A.424 B.421 C.420 D.403 二、填空题:本大题共 6小题,每小题 4分,共 24分. 11.(-2)-1 = . 12.一个不透明的袋子中装有 4个黑球,2个白球,每个 球除颜色外其他都相同,从中任意摸出 1个球是白 球的概率是 . 13.已知∠A是锐角,且 sinA=1 3,则 cosA= . 14.当 x=a与 x=b(a≠b)时,代数式 x2 -2x+3的值相 等,则 x=a+b时,代 数 式 x2 -2x+3的 值 为 . 15.如图,AB是⊙O的直径,点 E是 ) BF的中点,过点 E 的切线分别交 AF,AB的延长线于点 D,C,若∠C= 30°,⊙O的半径是 2,则图形中阴影部分的面积是 . 第 15题图 第 16题图 16.如图,在△ABC中,∠ABC=30°,AB=4,BC=5,P 是 32 △ABC内部的任意一点,连接 PA,PB,PC,则 PA+ PB+PC的最小值为 . 三、解答题:本大题共 9小题,共 86分. 17.(8分)解方程: x x-1-2 x=1. 18.(8分)先化简,再求值: x-2 1+2x+x2 ÷(x- 3x x+1),其 中 x=1 3. 19.(8分)在四边形 ABCD中,AB∥CD. (1)如图①,已知∠A=∠B,求证:AD=BC; (2)如图②,已知∠A=60°,∠B=45°,AD=2,求 BC 的长. 第 19题图 20.(8分)证明:三角形的中位线平行于三角形的第三 边,并且等于第三边的一半. (要求:在给出的△ABC中用尺规作出 AB,AC边的 中点 M,N,保留作图痕迹,不要求写作法,并根据图 形写出已知、求证和证明) 第 20题图 21.(8分) (1)计算: 1 1×2+ 1 2×3+ 1 3×4+ 1 4×5+ 1 5×6; (2)求证:1 3< 1 1×3+ 1 2×4+ 1 3×5+ 1 4×6<4 5. 22.(10分)小宝大学毕业后回家乡进行园艺创业,第一 期培植盆景与花卉各 50盆,售后进行统计得知:盆 景的平均每盆利润是 160元,花卉的平均每盆利润 是 20元.调研发现:①盆景每增加 1盆,盆景的平均 每盆利润减少 2元;每减少 1盆,盆景的平均每盆利 润增加 2元;②花卉的平均每盆利润始终不变.小宝 计划第二期培植盆景与花卉共 100盆,设培植的盆 景比第一期增加 x盆,第二期盆景与花卉售完后的 利润分别为 W1,W2(单位:元). (1)用含 x的代数式分别表示 W1,W2; (2)当 x取何值时,第二期培植的盆景与花卉售完 后获得的总利润 W最大?最大总利润是多少? 23.(10分)随着互联网、移动终端的迅速发展,数字化 阅读越来越普及.公交、地铁上的“低头族”越来越 多,某研究机构针对“您如何看待数字化阅读”问题 进行了随机问卷调查(问卷调查表如下图所示),并 将调查结果绘制成图①和图②所示的统计图(均不 完整). “您如何看待数字化阅读”问卷调查表 您好!这是一份关于“您如何看待数字化阅读” 问卷调查表,请在表格中选择一项您最认同的观点, 在其后空格内打“√”,非常感谢您的合作. 代码 观点 A 获取信息方便,可以随时随地观看 B 价格便宜易得 42 C 使得人们成为“低头族”,不利于人际交往 D 内容丰富,比纸质书涉猎更广 E 其他 第 23题图 请根据统计图中提供的信息,解答下列问题: (1)本次接受调查的总人数是 人,并将条 形统计图补充完整; (2)在 扇 形 统 计 图 中,观 点 E所 占 的 百 分 比 是 ,表 示 观 点 B的 扇 形 的 圆 心 角 度 数 为 度; (3)某市共有 300万人,请根据以上调查结果估算 该市持 A、B、D观点赞成数字化阅读的人数共有多 少万人. 24.(12分)如图,点 P是⊙O直径 AB上的一点,过点 P 作直线 CD⊥AB,分别交⊙O于 C,D两点,连接 AC,并 将线段 AC绕点 A逆时针旋转 90°得到线段 AE,连接 ED,分别交⊙O和 AB于点 F,G,连接 FC. (1)求证:∠ACF=∠AED; (2)若点 P在直径 AB上运动(不与点 A,B重合), 其它条件不变,请问EG AP是否为定值?若是,请求出 其值;若不是,请说明理由. 第 24题图 25.(14分)已知直线 y=x+t与双曲线 y=k x(k>0)交 于 C,D两点,过 C作 CA⊥x轴于点 A,过 D作 DB⊥ y轴于点 B,连接 AB. (1)求 C,D两点的坐标; (2)试探究直线 AB与 CD的位置关系并说明理由; (3)已知点 D(3,2),且 C,D在抛物线 y=ax2 +bx+ 5(a≠0)上,若当 m≤x≤n(其中 mn<0)时,函数 y =ax2 +bx+5的最小值为 2m,最大值为 2n,求 m+n 的值. 第 25题图 52 2019年三明市初中毕业班教学质量检测数学试题 (满分:150分 考试时间:5月 8日下午 15:00-17:00) 友情提示: 1.作图或画辅助线等需用签字笔描黑. 2.未注明精确度的计算问题,结果应为准确数 獉獉獉 . 一、选择题(共 10题,每题 4分,满分 40分.每题只有一 个正确选项,请在答题卡 獉獉獉 的相应位置填涂) 1.下列计算结果等于 -1的是 A.-1+2 B.(-1)0 C.-12 D.(-1)-2 2.第十六届海峡交易会对接合同项目 2049项,总投资 682亿元.将 682亿用科学记数法表示为 A.0.682×1011 B.6.82×1010 C.6.82×109 D.682×108 3.如图所示几何体的左视图是 4.一个不透明的袋子中只装有 4个黄球,它们除颜色外 完全相同,从中随机摸出一个球.下列说法正确的是 A.摸到红球的概率是 1 4 B.摸到红球是不可能事件 C.摸到红球是随机事件 D.摸到红球是必然事件 5.如图,已知 DE为△ABC的中位线,△ADE的面积为 3,则四边形 DECB的面积为 A.6 B.8 C.9 D.12 第 5题图 第 6题图 6.如图,点 A,B,C在小正方形的顶点上,且每个小正方 形的边长为 1,则 tan∠BAC的值为 A.槡3 3 B.槡3 C.1 2 D.1 7.若 2n+2n=1,则 n的值为 A.-1 B.-2 C.0 D.1 2 8.如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为 D,若 ⊙O的半径为 5,BC=8,则 AB的长为 第 8题图 A.8 B.10 槡C.4 3 D. 槡4 5 9.二次函数 y=x2 -6x+m满足以下 条件:当 -2<x<-1时,它的图 象位于 x轴的下方;当 8<x<9时,它的图象位于 x轴 的上方,则 m的值为 A.27 B.9 C.-7 D.-16 10.如图,四边形 ABCD为正方形,AB=1,把△ABC绕点 A逆时针旋转 60°得到△AEF,连接 DF,则 DF的长为 第 10题图 A.槡 槡6- 2 2 B.槡2-1 2 C.槡3 2 D.槡2 2 二、填空题(共 6题,每题 4分,满分 24分.请将答案填在 答题卡 獉獉獉 的相应位置) 第 11题图 11.如图,已知 a∥b,∠1=55°,则∠2 的度数是 . 12.某校准备从甲、乙、丙、丁四个科创 小组中选出一组,参加区青少年科 技创新大赛,下表反映的是各组平时成绩的平均数 x - (单位:分)及方差 s2.如果要选出一个成绩较好且状 态较 稳 定 的 小 组 去 参 赛,那 么 应 选 的 小 组 是 . 甲 乙 丙 丁 x 7 8 8 7 s2 1 1.2 0.9 1.8 13.不等式组 2x+4>0, x-3(x-2)≥{ 4 的解集是 . 62 14.程大位是我国珠算发明家.他的著作《直指算法统 宗》中记载了一个数学问题,大意是:有 100个和尚 分 100个馒头,如果大和尚 1人分 3个,小和尚 3人 分 1个,正好分完.问大、小和尚各有多少人?若设 大和尚有 x人,小和尚有 y人,则可列方程组为 . 15.如图,在矩形 ABCD中,AD=2,以点 A为圆心,AD长 为半径画弧,交 BC边于点 E,若 E恰为 BC的中点, 则图中阴影部分的面积为 . 第 15题图 第 16题图 16.如图,在直角坐标系中,四边形 OABC为菱形,OA在 x轴的正半轴上,∠AOC=60°,过点 C的反比例函数 y= 槡4 3 x的图象与 AB交于点 D,则△COD的面积为 . 三、解答题(共 9题,满分 86分.请将解答过程写在答题 獉獉 卡 獉 的相应位置,解答应写出文字说明、证明过程或演算 步骤) 17.(本题满分 8分) 先化简,再求值:(x-3x-4 x-1)÷x2 -4 x-1,其中 x=1 2. 18.(本题满分 8分) 如图,在菱形 ABCD中,对角线 AC与 BD交于点 O, DE∥AC,CE∥BD. 求证:四边形 OCED是矩形. 第 18题图 19.(本题满分 8分) 在平面直角坐标系中,直线 l经过点 A(-1,-4)和 B(1,0),求直线 l的函数表达式. 20.(本题满分 8分) 如图,在△ABC中,∠A=90°,AB=AC. (Ⅰ)请用尺规作图的方法在边 AC上确定点 P,使得 点 P到边 BC的距离等于 PA的长;(保留作图痕迹, 不写作法) (Ⅱ)在(Ⅰ)的条件下,求证:BC=AB+AP. 第 20题图 21.(本题满分 8分) 某景区的水上乐园有一批 4人座的自划船,每艘可 供 1至 4位游客乘坐游湖,因景区加大宣传,预计今 年游客将会增加,水上乐园的工作人员随机抽取了 去年某天中出租的 100艘次 4人自划船,统计了每艘 船的乘坐人数,制成了如下统计图. 抽查结果扇形统计图 第 21题图 (Ⅰ)扇形统计图中,“乘坐 1人”所对应的圆心角度 数为 ; (Ⅱ)所 抽 取 的 自 划 船 每 艘 乘 坐 人 数 的 中 位 数 是 ; (Ⅲ)若每天将增加游客 300人,那么每天需多安排 多少艘次 4人座的自划船才能满足需求 ? 72 22.(本题满分 10分) 惠好商场用 24000元购进某种玩具进行销售,由于深 受顾客喜爱,很快脱销,惠好商场又用 50000元购进 这种玩具,所购数量是第一次购进数量的 2倍,但每 套进价比第一次多了 10元. (Ⅰ)惠好商场第一次购进这种玩具多少套? (Ⅱ)惠好商场以每套 300元的价格销售这种玩具, 当第二次购进的玩具售出 4 5时,出现了滞销,商场决 定降价促销,若要使第二次购进的玩具销售利润率 不低于 12%,剩余的玩具每套售价至少要多少元? 23.(本题满分 10分) 如图,AB是⊙O的直径,点 D,E在⊙O上,∠B=2 ∠ADE,点 C在 BA的延长线上. (Ⅰ)若∠C=∠DAB,求证:CE是⊙O的切线; (Ⅱ)若 OF=2,AF=3,求 EF的长. 第 23题图 24.(本题满分 12分) 如图,在△ABC中,点 P是 BC边上的动点,点 M是 AP的中点,PD⊥AB,垂足为 D,PE⊥AC,垂足为 E,连 接 MD,ME. (Ⅰ)求证:∠DME=2∠BAC; (Ⅱ)若∠B=45°,∠C=75°,AB 槡=6 2,连接 DE,求 △MDE周长的最小值. 第 24题图 25.(本题满分 14分) 已知二次函数 y1 =mx2 -nx-m+n(m>0). (Ⅰ)求证:该函数图象与 x轴必有交点; (Ⅱ)若 m-n=3, (ⅰ)当 -m≤x<1时,二次函数的最大值小于 0,求 m的取值范围; (ⅱ)点 A(p,q)为函数 y2 =|mx2 -nx-m+n|图象上 的动点,当 -4<p<-1时,点 A在直线 y=-x+4 的上方,求 m的取值范围 . 82 2019年南平市初中毕业班适应性检测数学试题 (考试时间:120分钟;满分:150分) 第Ⅰ卷 一、选择题:本大题共 10小题,每小题 4分,共 40分.每 小题给出的四个选项中,只有一项是符合题目要求的. 1.实数 6的相反数是 ( ) A.-6 B.6 C.1 6 D.-1 6 2.下列图形既是轴对称图形,又是中心对称图形的是 ( ) A.三角形 B.菱形 C.角 D.平行四边形 3.小说《流浪地球》中提到“华北 794号地球发动机,全 功率运行时能向大地产生 15000000000吨的推力”. 这里的数据“15000000000”用科学记数法表示为 ( ) A.1.5×1012 B.1.5×1011 C.1.5×1010 D.150×108 第 4题图 4.如 图,在 ⊙O 中,∠ACB =34°,则 ∠AOB的度数是 ( ) A.17° B.34° C.56° D.68° 5.中国人最先使用负数,魏晋时期的数学家刘徽在“正 第 5题图 负术”的注文中指出,可将算 筹(小棍形状的记数工具)正 放表示正数,斜放表示负数. 如图,根据刘徽的这种表示 法,观察图①,可推算图②中 所得的数值为 ( ) A.-2 B.+2 C.-6 D.+6 6.下列说法正确的是 ( ) A.了解某型导弹杀伤力的情况应使用全面调查 B.一组数据 3,6,6,7,9的众数是 6 C.从 2000名学生中选 200名学生进行抽样调查,样 本容量为 2000 D.甲、乙两人在相同的条件下各射击 10次,他们成 绩的平均数相同,方差分别是 s2 甲 =0.3,s2 乙 =0.4, 则乙的成绩更稳定 7.如图,直线 AB∥CD,MN分别与 AB,CD交于点 E,F, 且∠AEM=50°,则∠DFN的大小为 ( ) 第 7题图 A.130° B.60° C.50° D.40° 8.如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC 内一点,将线段 CD绕点 C逆时针旋转 90°后得到 CE,连接 BE,若∠DAB=10°,则∠ABE是 ( ) 第 8题图 A.75° B.78° C.80° D.92° 9.现有甲,乙两种机器人都被用来搬运某体育馆室内装 潢材料,甲型机器人比乙型机器人每小时少搬运 30 千克,甲型机器人搬运 600千克所用的时间与乙型机 器人搬运 800千克所用的时间相同,两种机器人每小 时分别搬运多少千克?设甲型机器人每小时搬运 x 千克,根据题意,可列方程为 ( ) A.600 x = 800 x+30 B.600 x = 800 x-30 C. 600 x+30=800 x D. 600 x-30=800 x 10.如图,在△ABC中,AB=AC,BC=6,E为 AC边上的 点,且 AE=2EC,点 D在 BC边上且满足 BD=DE,设 BD=y,△ABC的面积 S△ABC =x,则 y与 x的函数关 系式为 ( ) 第 10题图 A.y= 1 810x2 +5 2 B.y= 4 810x2 +5 2 C.y= 1 810x2 +2 D.y= 4 810x2 +2 92 第Ⅱ卷 二、填空题:本题共 6小题,每小题 4分,共 24分. 11.分解因式:x2 +x= . 12.请写出一个比 1大且比 3小的无理数: . 13.一个凸多边形的内角和为 720°,则这个多边形的边 数是 . 14.已知扇形的弧长为 4π,半径为 8,则此扇形的面积为 . 15.n个数据 2,4,6,8,…,2n,这 组数 据的中 位数 是 (用含 n的代数式表示). 第 16题图 16. 已知,Rt△ABC中,∠ACB = 90°,AC=5,BC=12,点 D在 边 AB上,以 AD为直径的圆, 与边 BC有公共点 E,则 AD的 最小值是 . 三、解答题:本大题共 9小题,共 86分.解答题写出文字 说明、证明过程或演算步骤. 17.(本小题满分 8分) 计算:2sin30°-(π 槡- 2)0 槡+|3-1|+(1 2)-1. 18.(本小题满分 8分) 解不等式组: 2(x-2)<x-2① 3x>2x-1 { ② 19.(本小题满分 8分) 如图,ABCD的对角线 AC,BD相交于点 O,且 E, F,G,H分别是 AO,BO,CO,DO的中点.求证:四边 形 EFGH是平行四边形. 第 19题图 20.(本小题满分 8分) 某校开展以“学习朱子文化,弘扬理学思想”为主题 的读书月活动,并向学生征集读后感,学校将收到的 读后感篇数按年级进行统计,绘制了以下两幅统计 图(不完整). 第 20题图 根据图中提供的信息完成以下问题: (1)扇形统计图中“八年级”对应的圆心角是 度,并补全条形统计图; (2)经过评审,全校有 4篇读后感荣获特等奖,其中 有一篇来自七年级,学校准备从特等奖读后感中任 选两篇在校广播电台上播出,请利用画树状图或列 表的方法求出七年级特等奖读后感被校广播电台播 出的概率 . 03 21.(本小题满分 8分) 如图,AE∥BF,AC平分∠BAE,交 BF于点 C. (1)求证:AB=BC; (2)尺规作图:在 AE上找一点 D,使得四边形ABCD 为菱形(不写作法,保留作图痕迹). 第 21题图 22.(本小题满分 10分) 如图,已知反比例函数 y=m x的图象经过第一象限 内的一点 A(n,4),过点 A作 AB⊥x轴于点 B,且 △AOB的面积为 2. (1)求 m和 n的值; (2)若一次函数 y=kx+2的图象经过点 A,并且与 x 轴相交于点 C,求线段 AC的长. 第 22题图 23.(本小题满分 10分) 某超市为了扩大影响,对商品 A和 B进行打折促销. 打折前,买 60件 A商品和 30件 B商品用了 1080 元,买 50件 A商品和 10件 B商品用了 840元.打折 后,买 500件 A商品和 500件 B商品用了 9600元, 比不打折少花多少钱 ? 13 24.(本小题满分 12分) 如图,OA是⊙O的半径,点 E为圆内一点,且 OA⊥ OE,AB是⊙O的切线.EB交⊙O于点 F,BQ⊥AF 于点 Q. (1)如图①,求证:OE∥AB; (2)如图②,若 AB=AO,求AF BQ的值 ; (3)如图③,连接 OF,∠EOF的平分线交射线 AF于 点 P,若 OA=2,cos∠PAB=4 5,求 OP的长. 第 24题图 25.(本小题满分 14分) 已知 m,n分别是关于 x的一元二次方程 ax2 +bx+c =a与 ax2 +bx+c=b的一个根,且 m=n+1. (1)当 m=2,a=-1时,求 b与 c的值; (2)用只含字母 a,n的代数式表示 b; (3)当 a<0时,函数 y=ax2 +bx+c满足 b2 -4ac= a,b+c≥2a,n≤ -1 2,求 a的取值范围 . 23 书书书 2018—2019学年度福州市九年级质量检测 数学试题答案及评分标准 一、选择题:本题共 10小题,每小题 4分,满分 40分. 1.A 【解析】逐项分析如下: 选项 逐项分析 正误 A 既是轴对称图形,也是中心对称图形 √ B 既不是轴对称图形,也不是中心对称 图形 × C 既不是轴对称图形,也不是中心对称 图形 × D 既不是轴对称图形,也不是中心对称 图形 × 2.B 【解析】用科学记数法将一个绝对值大于 10的数 表示成 a×10n 的形式,其中 1≤a<10,故 a=1.1;n 是正整数,且 n等于原数的整数位数减 1,故 n=6-1 =5,故 110000用科学记数法表示为 1.1×105. 3.D 【解析】∵△ABC∽△DEF,且面积比为 4∶9,∴对 应高的比是 2∶3. 4.B 【解析】∵x2 =7,且 x为正数,∴x 槡= 7. 槡 槡∵ 4< 7 槡< 9, 槡∴2< 7<3. 第 5题解图 5.C 【解析】如解图,设 AC 与直线 a相交于点 D.∵ △ABC是 等 腰 直 角 三 角 形,∴∠ABC=45°.∵∠1 =15°,∴∠CBD=30°.∵a∥b,∴∠2=∠CBD=30°. 6.B 【解析】 槡 槡A.2 3×3 2=(2×3)槡 槡3×2=6 6,没 用到分配律;B.(ab)2 =a2b2 用到分配律;C.移项得, x=5-2,没有用到分配律;D.3a+2a=(3+2)a= 5a,没用到分配律. 7.C 【解析】∵袋中有 a个白球、b个红球、c个黄球, ∴袋中一共有(a+b+c)个球.∴摸出一个球是红球 的概率为 b a+b+c. 8.B 【解析】∵△ABC是等边三角形,∴∠A=∠B= ∠C=60°,AB=BC=AC=5.将△ADE沿 DE折叠, 点 A落在 BC边上的点 F处,∴△ADE≌△FDE.∴ ∠DFE=∠A=60°,AD=DF,AE=EF.设 BD=x,AE =EF=y,则 AD=DF=5-x,CE=5-y.∵BF=2,∴ CF=3.∵∠C=60°,∠DFE=60°,∠EFC+∠FEC= 120°,∠DFB+∠EFC=120°,∴∠DFB=∠FEC.∵ ∠C=∠B,∴△DBF∽△FCE.∴ DF FE=BD CF=BF CE,即 5-x y =x 3= 2 5-y.∴ 15-3x=xy 6=5x-{ xy ,解得 x=21 8 y=19{ 7 ,即 BD =21 8. 第 9题解图 9.C 【解析】如解图,过点 D作 DE⊥ AB 于 点 E.∵ ∠ACB = 90°,AC= 3,BC =4,∴ AB= AC2 +BC槡 2 =5.设 CD=x,则 BD=4-x,∵AD平分∠BAC,∴ DE=CD=x,AE=AC=3,则 BE =AB-AE=2.在 Rt△BDE中, BD2 =BE2 +DE2,∴(4-x)2 =22 +x2,解得 x=3 2,即 CD=3 2.∴S△ABD =1 2AB· DE=1 2 ×5×3 2 =15 4. ∵AD= AC2 +CD槡 2 = 槡3 5 2 ,设点 B到射线 AD的距离 是 h,∴S△ABD =1 2AD·h.∴h 槡= 5. 10.B 【解析】设该数学题集中有 x道难题,y道中档 题,z道容易题.由题意可得, x+y+z=100 ① x+2y+3z=180{ ② ,① × 2-②得 x-z=20道,∴难题比容易题多 20道,B选 项正确. 二、填空题:本题共 6小题,每小题 4分,满分 24分. 11.m(m+2)(m-2) 【解析】原式 =m(m2 -4)= m(m+2)(m-2). 12.正方体(答案不唯一) 13.甲 【解析】折线统计图的波动情况反映成绩的稳 定性,波动情况越小,成绩越稳定.由折线图可知甲 10次射击训练成绩为 9、7、8、9、8、9、7、9、9、9;乙 10 次射击训练成绩为 8、9、7、8、10、7、9、10、7、10,∴x甲 = 1 10(9+7+8+9+8+9+7+9+9+9)=8.4,x乙 = 1 10(8+9+7+8+10+7+9+10+7+10)=8.5.s2 甲 = 1 10[(9-8.4)2 +(7-8.4)2 +(8-8.4)2 +(9- 8.4)2 +(8-8.4)2+(9-8.4)2 +(7-8.4)2 +(9- 8.4)2 +(9-8.4)2 +(9-8.4)2]=0.64,s2 乙 = 1 10[(8-8.5)2 +(9-8.5)2 +(7-8.5)2 +(8- 8.5)2+(10-8.5)2+(7-8.5)2+(9-8.5)2+( 10- 1 8.5)2 +(7-8.5)2 +(10-8.5)2]=1.45.∵s2 甲 < s2 乙 .∴这 10次射击成绩更稳定的运动员是甲. 14.4 【解析】∵原式 =-m+5+1 m-5 =-m+5 m-5 + 1 m-5= -1+ 1 m-5,分式 -m+6 m-5的值是负整数,∴ 1 m-5是 负整数.∵m是整数,∴m-5=-1.∴m=4. 第 15题解图 15. 槡4 3 【解析】如解图,直 线 y=kx+2k+3必过点 C (-2,3),∴最短的弦 AB 是过点 C且与 OC垂直的 弦.∵C(-2,3),∴OC= 槡13.∵⊙O的半径为 5, ∴ 在 Rt△OBC中,BC= OB2 -OC槡 2 槡=2 3.∴弦 AB长的最小值为 槡4 3. 第 16题解图 16.槡5+1 2 【解析】如解图,过点 C作 CD⊥OB于点 D,过点 A作 AF⊥y 轴于点 F交 DC延长线于点 E.∵ ∠OAB=45°,OC⊥ AB,∴ OC= CA,∠ODC=∠E=90°.∵∠ACE =∠BCD,∠OCD+∠BCD=90°,∠OCD+∠COD= 90°,∴ ∠COD =∠BCD.∴ ∠COD =∠ACE.∴ △ACE≌△COD(AAS),∴OD=CE,CD=AE.设 C (1,k),则 OD=CE=1,CD=AE=k.∴AF=1-k, OF=1+k.∴(1+k)(1-k)=k,解得 k=槡5-1 2 (负 值已舍去).∵CD⊥OB,∠COD=∠BCD,∴∠ABO= ∠OCD, tan∠ABO = tan∠OCD = OD CD = 1 槡5-1 2 =槡5+1 2 . 三、解答题:本题共 9小题,共 86分.解答应写出文字说 明、证明过程和演算步骤. 17.解:原式 槡=3+ 3×槡3 3-1 6分!!!!!!!!! =3+1-1 7分!!!!!!!!!!! =3. 8分!!!!!!!!!!!!!! 18.证明:∵∠1=∠2, ∴∠ACB=∠ACD. 3分!!!!!!!!!!! 在△ABC和△ADC中, ∠B=∠D, ∠ACB=∠ACD, AC=AC{ , ∴△ABC≌△ADC(AAS). 6分!!!!!!!! ∴CB=CD. 8分!!!!!!!!!!!!!! 19.解:原式 =x-1 x ÷x2 -2x+1 x2 1分!!!!!!!! =x-1 x · x2 (x-1)2 3分!!!!!!!! = x x-1, 5分!!!!!!!!!!!! 当 x 槡= 3+1时,原式 = 槡3+1 槡3+1-1 6分!!!!! =槡3+1 槡3 = 槡3+ 3 3 . 8分!!!!!! 20.解:如解图,⊙O就是所求作的圆. 3分!!!!! 第 20题解图 4分!!!!!!!!!!!!!!!!!!! 证明:如解图,连接 OD. ∵BD平分∠ABC, ∴∠CBD=∠ABD. 5分!!!!!!!!!!! ∵OB=OD, ∴∠OBD=∠ODB. ∴∠CBD=∠ODB. 6分!!!!!!!!!!! ∴OD∥BC. ∴∠ODA=∠ACB. 又∠ACB=90°, ∴∠ODA=90°. 即 OD⊥AC. 7分!!!!!!!!!!!!!! ∵点 D是半径 OD的外端点, ∴AC与⊙O相切. 8分!!!!!!!!!!!! 21.解:(1)四边形 ABB′A′是菱形. 1分!!!!!! 证明如下:由平移得 AB∥A′B′,AB=A′B′, ∴四边形 ABB′A′是平行四边形,∠AA′B=∠A′BC. 2分!!!!!!!!!!!!!!!!!! ∵BA′平分∠ABC, ∴∠ABA′=∠A′BC. ∴∠AA′B=∠A′BA. 3分!!!!!!!!!!! ∴AB=AA′. ∴ABB′A′是菱形; 4分!!!!!!!!!!! (2)如解图,过点 A作 AF⊥BC于点 F. 由(1)得 BB′=BA=6. 由平移得△A′B′C′≌△ABC , 2 第 21题解图 ∴B′C′=BC=4. ∴BC′=10. 5分!!! ∵AC′⊥A′B′, ∴∠B′EC′=90°. ∵AB∥A′B′, ∴∠BAC′=∠B′EC′=90°. 在 Rt△ABC′中,AC′= BC′2 -AB槡 2 =8. 6分!!! ∵S△ABC′=1 2AB·AC′=1 2BC′·AF, ∴AF=AB·AC′ BC′ =24 5. 7分!!!!!!!!!! ∴S菱形ABB′A′=BB′·AF=144 5. ∴菱形 ABB′A′的面积是144 5. 8分!!!!!!! 22.解:(1)是; 2分!!!!!!!!!!!!!!! (2)①85.5;336; 6分!!!!!!!!!!!! ②由表中数据可知,30名同学中,A等级的有 10人, B等级的有 11人,C等级的有 5人,D等级的 有 4人. 依题意得,15×4+10×5+5×11+0×10 30 8分!! =5.5. 9分!!!!!!!!!!!! ∴根据算得的样本数据提高的平均成绩,可以估计, 强化训练后,全年级学生的平均成绩约提高 5.5分. 10分!!!!!!!!!!!!!!!!! 23.解:(1)y=27-25-0.1(x-2)=-0.1x+2.2; 4分 ! !!!!!!!!!!!!!!!!!!!! (2)依题意,得(-0.1x+2.2)x+0.5×10+1×(x- 10)=20.6, 7分!!!!!!!!!!!!!! 解得 x1 =x2 =16. 9分!!!!!!!!!!!! 答:x的值是 16. 10分!!!!!!!!!!!! 24.(1)①证明:∵四边形 ABCD是正方形, ∴∠ADC=∠BCD=90°,CA平分∠BCD. ∵EF⊥EB, ∴∠BEF=90°. 证法一:如解图①,过点 E作 EN⊥BC于点 N, 1分 !! !!!!!!!!!!!!!!!!!! ∴∠ENB=∠ENC=90°. ∵四边形 AEGD是平行四边形, ∴AD∥GE. ∴∠EMF=∠ADC=90°. ∴EM⊥CD,∠MEN=90°. ∴EM=EN. 2分!!!!!!!!!!!!!! ∵∠BEF=90°, ∴∠MEF=∠BEN. ∴△EFM≌△EBN(ASA). ∴EB=EF. 3分!!!!!!!!!!!!!! 第 24题解图① 第 24题解图② 证法二:如解图②,过点 E作 EK⊥AC交 CD延长线 于点 K, 1分!!!!!!!!!!!!!!!! ∴∠KEC=∠BEF=90°. ∴∠BEC=∠KEF. ∵∠BEF+∠BCD=180°, ∴∠CBE+∠CFE=180°. ∵∠EFK+∠CFE=180°, ∴∠CBE=∠KFE. 又∠ECK=1 2∠BCD=45°, ∴∠K=45°. ∴∠K=∠ECK. ∴EC=EK. 2分!!!!!!!!!!!!!! ∴△EBC≌△EFK(AAS). ∴EB=EF. 3分!!!!!!!!!!!!!! 证法三:如解图③,连接 BF,取 BF中点 O,连接 OE, OC. 1分!!!!!!!!!!!!!!!!!! ∵∠BEF=∠BCF=90°, ∴OE=1 2BF=OC. ∴点 B,C,E,F都在 以 O为圆心,OB为半径的⊙O上. ∵ ) BE= ) BE, ∴∠BFE=∠BCA=45°. 2分!!!!!!!!! ∴∠EBF=45°=∠BFE. ∴EB=EF. 3分!!!!!!!!!!!!!! 第 24题解图③ 第 24题解图④ ②GH⊥AC. 4分!!!!!!!!!!!!!! 证明如下:如解图④, ∵四边形 ABCD是正方形, 四边形 AEGD是平行四边形, ∴AE=DG,EG=AD=AB,AE∥DG, ∠DGE=∠DAC=∠DCA=45°. ∴∠GDC=∠ACD=45°. 5分 !!!!!!!!! 3 由(1)可知, ∠GEF=∠BEN,EF=EB. ∵EN∥AB, ∴∠ABE=∠BEN=∠GEF. ∴△EFG≌△BEA(SAS). 6分!!!!!!!! ∴GF=AE=DG. ∴∠GFD=∠GDF=45°. ∴∠CFH=∠GFD=45°. ∴∠FHC=90°. ∴GH⊥AC. 7分!!!!!!!!!!!!!! (2)解:如解图⑤,过点 B作 BQ⊥BP,交直线 AP于 点 Q,取 AC中点 O, ∴∠PBQ=∠ABC=90°. ∵AP⊥CG, ∴∠APC=90°. ①如解图⑤,当点 E在线段 AO上时,(或“当 0<AE <1 2AC时”) ∠PBQ-∠ABP=∠ABC-∠ABP, 即∠QBA=∠PBC. 8分!!!!!!!!!!! ∵∠ABC=∠APC=90°, ∴∠BCP+∠BAP=180°. ∵∠BAP+∠BAQ=180°, ∴∠BAQ=∠BCP. 9分!!!!!!!!!!! ∵BA=BC, ∴△BAQ≌△BCP(ASA). 10分!!!!!!!! ∴BQ=BP=10,AQ=CP. 在 Rt△PBQ中,PQ= BP2 +BQ槡 2 槡=10 2. ∴PA+PC=PA+AQ=PQ 槡=10 2. 11分!!!! 第 24题解图⑤ 第 24题解图⑥ ②如解图⑥,AP与 BC交于点 K,当点 E在线段 OC 上时,(或“当 1 2AC<AE<AC时”)∠PBQ-∠QBC =∠ABC-∠QBC, 即∠QBA=∠PBC. ∵∠ABC=∠APC=90°,∠AKB=∠CKP, ∴∠BAQ=∠BCP. 12分!!!!!!!!!!! ∵BA=BC, ∴△BAQ≌△BCP(ASA). ∴BQ=BP=10,AQ=CP. 在 Rt△PBQ中,PQ= BP2 +BQ槡 2 槡=10 2. ∴PA-PC=PA-AQ=PQ 槡=10 2. 13分!!!! 综上所述,当点 E在线段 AO上时,PA+PC 槡=10 2; 当点 E在线段 OC上时,PA-PC 槡=10 2. 25.解:(1)B(m,0),C(0,5 2m); 2分!!!!!!! (2)设点 E,F的坐标分别为(a,a 2),(-a,-a 2), 3分!!!!!!!!!!!!!!!!!! 代入 y=-1 2(x+5)(x-m)=-1 2x2+1 2(m-5)x+ 5 2m, 得 -1 2a2 +1 2(m-5)a+5 2m=a 2 ① -1 2a2 -1 2(m-5)a+5 2m=-a 2{ ② , 4分! 由① -②,得(m-5)a=a. ∵a≠0, ∴m=6. 5分!!!!!!!!!!!!!!!! ∴抛物线的解析式为 y=-1 2x2 +1 2x+15. 6分 !! !!!!!!!!!!!!!!!!!! (3)依题意得 A(-5,0),C(0,5 2m), 由 m>0,设过 A,C两点的一次函数解析式是 y=kx+ b, 将 A,C代入,得 -5k+b=0 b=5 2{ m ,解得 k=1 2m b=5 2{ m , ∴过 A,C两点的一次函数解析式是 y=1 2mx+5 2m. 7分!!!!!!!!!!!!!!!!!! 设点 P(t,0),则 -5≤t≤m(m>0), ∴M(t,-1 2t2+1 2(m-5)t+5 2m),N(t,1 2mt+5 2m). ①当 -5≤t≤0时, ∴MN =-1 2t2 +1 2(m-5)t+5 2m-(1 2mt+5 2m) =-1 2t2 -5 2t. 8分!!!!!!!!!! ∵ -1 2<0,∴该二次函数图象开口向下, 又对称轴是直线 t=-5 2, ∴当 t=-5 2时,MN的长最大 , 4 此时 MN=-1 2×(-5 2) 2 -5 2×(-5 2)=25 8. 9分 ! !!!!!!!!!!!!!!!!!! ②当 0<t≤m时, ∴MN =1 2mt+5 2m-[-1 2t2 +1 2(m-5)t+5 2m] =1 2t2 +5 2t. 10分!!!!!!!!!!! ∵ 1 2>0,∴该二次函数图象开口向上. 又∵对称轴是直线 t=-5 2, ∴当 0<t≤m时,MN的长随 t的增大而增大, ∴当 t=m时,MN的长最大,此时 MN=1 2m2+5 2m. 11分!!!!!!!!!!!!!!!!! ∵线段 MN长的最大值为25 8, ∴ 1 2m2 +5 2m≤25 8, 12分!!!!!!!!!! 整理得(m+5 2) 2 ≤50 4, 由图象可得 槡-5-5 2 2 ≤m≤ 槡-5+5 2 2 . ∵m>0, ∴m的取值范围是 0<m≤ 槡-5+5 2 2 . 13分 !!! 5 2019年厦门市初中毕业班教学质量检测数学参考答案 一、选择题(本大题有 10小题,每小题 4分,共 40分) 1.B 2.A 【解析】∵BC,AB分别是∠A的对边和直角三角 形的斜边,∴根据锐角三角形函数的定义可知,BC AB =sinA. 3.C 【解析】∵点 A在第一象限,∴设点 A的坐标为 (x,y),其中 x,y均大于 0,∴点 A关于原点的中心 对称点的坐标为(-x,-y),根据平面直角坐标内点 的坐标特征可知,该点在第三象限. 4.D 【解析】由题意得 n≥0,故选项 A错误; 2.槡 5= 槡5 2=槡10 2 ,为无理数,故选项 B错误;槡 槡8=2 2,为 无理数,故选项 C错误;槡9=3,为有理数,故选项 D 正确. 5.B 【解析】∵AF∥BC,且 AD⊥AF,AD⊥BC,∴AD的 长为平行线 AF和 BC之间的距离. 6.C 【解析】A.该圆的直径不是直角三角形的直角 边,故 A错误;B.该圆的半径是直角三角形的直角 边,而不是直径,故 B错误;C.直角三角形的一个直 角边与该圆相切,另一条直角边是该圆的直径,故 C 正确;D.直角三角形的两条直角边都没有与圆相切, 故 D错误. 7.A 【解析】方程(x-m)(x-a)=0的解是 x1 =m,x2 =a,∵x1 =x2 =m,则 a=m,且 a是该方程的根. 8.D 【解析】由题意可知 P(摸出白球)= a a+b+c= 1 3,∴3a=a+b+c,整理得 a=1 2(b+c). 9.C 【解析】∵点 E还有三次落在菱形的边上,且不 包括点 E与点 B重合,∴点 E可分别落在 BC、CD、 AD上,∵无论∠B为何值,在旋转的过程中,点 E都 会与点 D重合,即落在 AD边上,故要分别在边 BC、 CD上找一动点 E,使得 AE=AB,如解图①,当∠B= 60°时,易得△ABC是等边三角形,则 AC=BC,此时 在 BC、CD边上任取一点 E,AE恒小于 AB,故当∠B >60°时,AC>AB,此时在 BC、CD上分别存在一点 E,使得 AE=AB,如解图②,当∠B=90°时,根据直角 三角形的性质,在 BC、CD在分别任取一点 E,此时 AE>AB=AD,故∠B<90°,∴60°<α<90°. 第 9题解图 10.C 【解析】由题意得二次函数图象的对称轴为直线 x=- 2 2×(-3)=1 3,∵dA <1 2<dB <dC,且 a,b,c 均大于 0,∴点 B,C一定在抛物线对称轴的右侧, 点 A的位置不确定,∴当 b≤x≤c时,y随 x的增大 而减小. 二、填空题(本大题有 6小题,每小题 4分,共 24分) 11.2a 【解析】原式 =(-1+3)a=2a. 12.x≥ 3 2 【解析】移项得 2x≥3,解得 x≥ 3 2. 13.(8,3) 【解析】∵四边形 ABCD是平行四边形,∴ AD=BC,AD∥BC,∵B(1,-1),C(7,-1),∴BC= 6,∴AD=6,∵AD∥BC,A(2,3),∴D(8,3). 14.18 【解析】∵想让一半左右的营业员都能达到月 销售目标,∴这一半左右员工的月均销售额应大于 月销售目标,故月销售目标定中位数比较合适,即 18万元. 15.1 3 【解析】∵OD=3OC,∴点 B在点 A的右侧,作 示意图如解图,延长 BE交 y轴于点 F,∵点 A在 y =x的图象上,∴设点 A的坐标为(a,a),即 OC= AC=a,∵OD=3OC,∴OD=3a,设 B(3a,b),∵点 A,B均在反比例函数的图象上,∴3ab=a2,解得 b =1 3a,即 BD=1 3a,∵AC=a,∴AE=AC-BD=2 3 a,∵OD=3a,OC=a,∴BE=CD=2a,在 Rt△ABE 中,tan∠ABE=AE BE= 2 3a 2a=1 3. 第 15题解图 第 16题解图 16. 槡4-2 2 【解析】如解图,连接 BM,由题意可知 BE =AB,∵四边形 ABCD是矩形,∴∠ABC=∠BCM= 90°,AB=CD,∵BE=AB,∴BE=CD,∵DM=CE, ∴BC=CM,∴ ∠MBC=45°,∵ ) AE的长 为 2π,∴ 90π×AB 180 =2π,解得 AB=4,∴BM =BE=4,在 Rt △BCM中,BC=BM·cos45° 槡=2 2,∴CE=BE- BC 槡=4-2 2. 三、解答题(本大题有 9小题,共 86分 ) 6 17.解: x+y=4,①, x-2y=1.{ ② ① -②得 (x+y)-(x-2y)=4-1, 2分!!!!!!!! y+2y=3, 3分!!!!!!!!!!!!!!! 3y=3, 4分!!!!!!!!!!!!!!!! y=1. 5分!!!!!!!!!!!!!!!!! 把 y=1代入①得 x+1=4, x=3. 7分!!!!!!!!!!!!!!!!! ∴这个方程组的解是 x=3, y=1{ . 8分!!!!!!!!!!!!!!!! 18.证明(方法一): ∵AB∥FC, ∴∠B=∠FCE. 2分!!!!!!!!!!!! ∵BC=DE,点 B,C,D,E在一条直线上, ∴BC+CD=DE+CD. 即 BD=CE. 4分!!!!!!!!!!!!! 又∵AB=FC, ∴△ABD≌△FCE(SAS). 6分!!!!!!!! ∴∠ADB=∠E. 7分!!!!!!!!!!!! ∴AD∥FE. 8分!!!!!!!!!!!!!! 证明(方法二): 第 18题解图 如解图,连接 AF. ∵AB∥FC,AB=FC, ∴四边形 ABCF是平行四边 形. 2分!!!!!!!! ∴AF∥BC,AF=BC. 4分 !! !!!!!!!! ∵BC=DE, ∴AF=DE. 5分!!!!!!!!!!!!!! 又∵B,C,D,E在一条直线上, ∴AF∥DE. ∴四边形 ADEF是平行四边形. 7分!!!!!! ∴AD∥FE. 8分!!!!!!!!!!!!!! 19.解:原式 =2a2 -4-a2 a2 · a2 a2 +2a 2分!!!!!! =(a+2)(a-2) a2 · a2 a(a+2) =a-2 a . 6分!!!!!!!!!!!! 当 a 槡= 2时,原式 =槡2-2 槡2 7分!!!!!!!! 槡=1- 2. 8分!!!!!!!!!!!!!!! 20.解:(1)如解图,点 E即为所求; 3分!!!!!! 第 20题解图 (2)方法一: ∵四边形 ABCD是正方形, ∴∠BCD=90°,BC=CD. ∴∠DBC=∠CDB=45°. 5分!!!!!!!! ∵EF⊥BD, ∴∠BFE=90°. 由(1)得 EF=EC,BE=BE, ∴Rt△BFE≌Rt△BCE. 6分!!!!!!!!! ∴BC=BF. ∴∠BCF=∠BFC. 7分!!!!!!!!!!! ∴∠BCF=180°-∠FBC 2 =67.5°. 8分!!!!! 方法二: ∵四边形 ABCD是正方形, ∴∠BCD=90°,BC=CD. ∴∠DBC=∠CDB=45°. 5分!!!!!!!! 由(1)得 EF=EC, ∴∠EFC=∠ECF. 6分!!!!!!!!!!! ∵EF⊥BD, ∴∠BFE=90°. ∵∠BFE=∠BCE=90°, ∴∠BFE-∠EFC=∠BCE-∠ECF. ∴∠BFC=∠BCF. 7分!!!!!!!!!!! ∵∠DBC=45°, ∴∠BCF=180°-∠FBC 2 =67.5°. 8分!!!!! 21.解:(1)该日停留时间为 10s~12s的车辆约有 7 辆,这些停留时间为 10s~12s的车辆的平均停留 时间约为 11s; 3分!!!!!!!!!!!!! (2)依题意,车辆在 A斑马线前停留时间约为: 1×10+3×12+5×12+7×8+9×7+11×1 50 = 4. 72s. 车辆在 B斑马线前停留时间为: 1×3+3×2+5×10+7×13+9×12 40 =6.45s. 7分 ! !!!!!!!!!!!!!!!!!! ∵4.72<6.45, ∴移动红绿灯放置在 B斑马线上较为合适. 8分 !! !!!!!!!!!!!!!!!!!! 22.解:(1)∵∠C=90°, ∴AB为△ABC外接圆的直径. 1分!!!!!! ∵该圆的半径为 槡5 2 , 7 ∴AB 槡=10 2. 2分!!!!!!!!!!!!! ∴在 Rt△ABC中,AC2 +BC2 =AB2. ∵AC=10. ∴102 +BC2 =( 槡10 2)2. ∴BC=10. 4分!!!!!!!!!!!!!! ∴AC=BC. ∴∠A=∠B. ∴∠A=180°-∠C 2 =45°; 5分!!!!!!!! (2)AB与 CD互相垂直,理由如下: 由(1)得,AB为外接圆的直径,取 AB中点 O,则点 O为圆心,如解图,连接 OC,OD. ∵CE⊥DB, 第 22题解图 ∴ 在 Rt△CBE中,BE2 +CE2 =BC2. 即 32 +42 =BC2. ∴BC=5. 6分!!!!!!! ∵ ) BC= ) BC, ∴∠A=∠CDE. 7分!!!!!!!!!!!! ∵∠ACB=90°, ∴在 Rt△ACB中,tanA=BC AC=5 10=1 2. ∴tan∠CDE=tanA=1 2. 8分!!!!!!!!! 又∵在 Rt△CED中,tan∠CDE=CE DE, ∴CE DE=1 2,即 4 DE=1 2. ∴DE=8. ∴BD=DE-BE=8-3=5. ∴BC=BD. 9分!!!!!!!!!!!!!! ∴∠BOC=∠BOD. ∵OC=OD, ∴OM⊥CD. 即 AB⊥CD. 10分!!!!!!!!!!!!! 第 23题解图① 23.解:(1)如解图 ①,过 点 D作 DE⊥BC,则∠DEB=90°. ∵AB∥CD, ∴∠ABC=∠DCE=60°. 1分 !! !!!!!!!!! ∴在 Rt△CDE中,sin∠DCE=DE CD, ∴DE=sin60°×3= 槡3 3 2 . 3分!!!!!!!! ∴S△BCD =1 2BC·DE=1 2×4× 槡3 3 2 槡=3 3; 4分 !!! !!!!!!!!!!!!!!!!! (2)方法一:如解图②,连接 AN,AC, ∵线段 BM绕点 B逆时针旋转 60°得到线段 BN, ∴NB=MB,∠NBM=60°. ∵∠MBC+∠MBA=∠MBA+∠NBA. 第 23题解图② ∴∠MBC=∠NBA, ∵AB=BC, ∴△MBC≌△NBA(SAS). 5分 ! !!!!!!!!! ∴∠NAB=∠MCB=120°. ∵∠ABC=60°,AB=BC, ∴△ABC为等边三角形. 6分!!!!!!!! ∴∠BAC=∠ACB=60°. ∴∠NAB+∠BAC=180°. ∴N,A,C三点在一条直线上. 7分!!!!!! ∵NQ=n,BQ=m, ∴CQ=4-m. ∵NQ⊥BC, ∴∠NQC=90°. ∴在 Rt△NQC中,NQ=CQ·tan∠NCQ. ∴n 槡= 3(4-m). 即 n 槡=- 3m 槡+4 3. 9分!!!!!!!!!! ∴n关于 m的函数解析式为:n 槡=- 3m 槡+4 3(1 2 ≤m≤2). 10分!!!!!!!!!!!!!! 第 23题解图③ 方法二:如解图③,连接 AN, ∵线段 BM绕点 B逆时针旋转 60°得到线段 BN, ∴NB=BM,∠NBM=60°. ∵ ∠MBC +∠MBA =∠MBA +∠NBA. ∴∠MBC=∠NBA, ∵AB=BC, ∴△MBC≌△NBA. 5分!!!!!!!!!!! ∴∠NAB=∠MCB=120°. 设 AB与 NQ交于 H点, ∵NQ⊥BC, ∴∠HQB=90°. ∵∠ABC=60°, ∴∠BHQ=∠NHA=30°. ∴∠HNA=180°-30°-120°=30°. ∴NA=AH. 6分!!!!!!!!!!!!!! ∴在 Rt△BHQ中,HQ=BQ·tan∠HBQ 槡= 3m. 7分 ! !!!!!!!!!!!!!!!!! 又∵BH=2m, ∴AH=4-2m. 过点 A作 AG⊥NH, ∴NG= GH. 8 在 Rt△AGH中,GH=AH·cos∠AHN=槡3 2(4-2m) 槡 槡=2 3- 3m. 8分!!!!!!!!!!!!! ∴NH=2GH 槡 槡=4 3-2 3m. ∵NQ=NH+HQ, ∴n 槡=- 3m 槡+4 3. 9分!!!!!!!!!!! ∴n关于 m的函数解析式为:n 槡=- 3m 槡+4 3(1 2 ≤m≤2). 10分!!!!!!!!!!!!!! 24.解:(1)由题意得 T=22- h 100×0.5, 即 T=- 1 200h+22(0≤h≤1000). 3分!!!!! ∵ - 1 200<0,∴T随 h的增大而减小. ∴当 h=1000m时,T有最小值 17℃; 4分!!! (2)根据表一的数据可知,当 19≤T≤21时,成活率 p与温度 T之间的关系大致符合一次函数关系,不 妨设 p1 =k1T+b1;当 17.5≤T<19时,成活率 p与 温度 T之间的关系大致符合一次函数关系,不妨设 p2 =k2T+b2. 5分!!!!!!!!!!!!! ∵当 T=21时,p1 =0.9;当 T=20时,p1 =0.94, 解得 k1 =-1 25, b1 =87 50{ , ∴p1 =-1 25T+87 50(19≤T≤21). 6分!!!!! ∵当 T=19时,p2 =0.98;当 T=18时,p2 =0.94, 解得 k2 =1 25, b2 =11 50{ , ∴p2 =1 25T+11 50(17.5≤T<19). 7分!!!!! 由图可得,除点 E外,其余点大致在一条直线上.因 此,当 0≤h≤1000时,可估计种植量 w与山高 h之 间的关系大致符合一次函数关系,不妨设 w=k3h+ b3. 8分!!!!!!!!!!!!!!!!!! ∵当 h=200时,w=1600;当 h=300时,w=1400, 解得 k3 =-2, b3 =2000{ , ∴w=-2h+2000(0≤h≤1000). 9分!!!!! 考虑到成活率 p不低于 92%, 则 17.5≤T≤20.5 由 T=- 1 200h+22,可知 T为 17.5℃,19℃,20.5℃ 时,h分别为 900m,600m,300m. 由一次函数增减性可知: 当 300≤h≤600时,p1 =-1 25T+87 50=-1 25(- 1 200h +22)+87 50= 1 5000h+43 50. 当 600<h≤900时,p2 =1 25T+11 50=1 25(- 1 200h+ 22)+11 50=- 1 5000h+11 10. ∴当 300≤h≤600时, 成活量 =w·p1 =(-2h+2000)·( 1 5000h+43 50). 10分!!!!!!!!!!!!!!!!! ∵ - 1 2500<0,对称轴在 y轴左侧, ∴当 300≤h≤600时,成活量随 h的增大而减小. ∴当 h=300时,成活量最大. 根据统计结果中的数据,可知 h=300时成活率为 92%,种植量为 1400株, ∴此时最大成活量为 1400×92% =1288(株). 11分 ! !!!!!!!!!!!!!!!!! 当 600<h≤900时, 成活量 =w·p2 =(-2h+2000)·(- 1 5000h+11 10). ∵ 1 2500>0,对称轴在 h=900的右侧, ∴当 600<h≤900时,成活量随 h的增大而减小. 且当 h=600时,w·p1 =w·p2 综上,可知当 h=300时,成活量最大. ∴山高 h为 300米时该作物的成活量最大. 12分 !! !!!!!!!!!!!!!!!!! 25.解:(1)A(4,-6)或(-4,6). 3分!!!!!!! (2)① E(1,-1)不 是点 N的 对称 位似 点,理 由 如下: 设 A1(x1,y1),A2(x2,y2),由题可知 |x2 x1 |=|y2 y1 |= OA2 OA1 =q. 当 k=1 2时,2k-2=-1. 把 y=-1,k=1 2分别代入 y=kx-2,可得 x=2. 可得 N(2,-1). 5分!!!!!!!!!!!! ∴N(2,-1)关于 x轴的对称点 N1(2,1). 6分! ∵对于 E(1,-1),|-1 1 |≠ |1 2|, ∴不存在 q,使得 E(1,-1)是点 N的对称位似点. ∴E(1,-1)不是点 N的对称位似点; 7分!!! ②点 M的对称位似点可能仍在抛物线 C上,理由 如下 : 9 方法一: 把 N(m(m-k) k2 ,2k-2)代入 y=kx-2, 可得 m2 -mk-2k2 =0. (m-2k)(m+k)=0. ∴m=2k或 m=-k. 8分!!!!!!!!!! 当直线与抛物线图象相交时,有 kx-2=-1 2x2 + mx-2. 即 kx=-1 2x2 +mx. ∵x≠0,∴k=-1 2x+m. ∴x1 =2(m-k). 抛物线 C的对称轴为直线 x=m. ∵点 M不是抛物线的顶点,∴2(m-k)≠m, ∴m≠2k. ∴m=-k. 9分!!!!!!!!!!!!!! ∴x1 =-4k, 可得 M(-4k,-4k2 -2), ∴点 M关于 x轴的对称点坐标为 M1(-4k,4k2 + 2). 10分!!!!!!!!!!!!!!!!! 设点 M的对称位似点 M2 为(-4kq,4k2q+2q)或 (4kq,-4k2q-2q). 11分!!!!!!!!!! 当 M2 为(4kq,-4k2q-2q)时, 将点 M2(4kq,-4k2q-2q)代入 y=-1 2x2 -kx-2. 可得 8k2q2 -2q+2=0,即 4k2q2 -q+1=0. 12分 !!! !!!!!!!!!!!!!!!!! 当 Δ≥0,即 k2≤ 1 16时, q=1± 1-16k槡 2 8k2 >0符合题意. ∵m>0,m=-k, ∴k<0. 又∵k2≤ 1 16, ∴ -1 4≤k<0. ∴当 -1 4≤k<0时,点 M的对称位似点仍在抛物 线 C上. 14分!!!!!!!!!!!!!!! 方法二: 把 N(m(m-k) k2 ),2k-2)代入 y=kx-2 可得 m2 -mk-2k2 =0. (m-2k)(m+k)=0. ∴m=2k或 m=-k. 8分!!!!!!!!!! 当直线与抛物线图象相交时,有 kx-2=-1 2x2 + mx-2. 即 kx=-1 2x2 +mx. ∵x≠0,∴k=-1 2x+m. ∴x1 =2(m-k). 抛物线 C的对称轴为直线 x=m. ∵点 M不是抛物线的顶点,∴2(m-k)≠m, ∴m≠2k. ∴m=-k. 9分!!!!!!!!!!!!!! ∴x1 =-4k, 可得 M(-4k,-4k2 -2) ∴点 M关于 x轴的对称点坐标为 M1(-4k,4k2 + 2). 10分!!!!!!!!!!!!!!!!! 设直线 OM1 的表达式为 y=nx,把 M1(-4k,4k2 + 2)代入 y=nx, 可得 y=4k2 +2 -4kx. 11分!!!!!!!!!!! 若直线 OM1 与抛物线 C相交,有4k2 +2 -4kx=-1 2x2 -kx-2. 12分!!!!!!!!!!!!!!! 化简可得 2kx2 -2x+8k=0,即 kx2 -x+4k=0. 当 Δ≥0,即 k2≤ 1 16时,二者有交点. 设交点为 M2,此时令OM2 OM1 =q,则 M2 是点 M的对称 点位似点. ∵m>0,m=-k, ∴k<0. 又∵k2≤ 1 16, ∴ -1 4≤k<0. ∴当 -1 4≤k<0时,点 M的对称位似点仍在抛物 线 C上. 14分 !!!!!!!!!!!!!!! 01 2019泉州市初中学业质量检查 一、选择题 1.D 2.C 【解析】逐项分析如下: 选项 逐项分析 正误 A a+a+a=3a B a5 与 a2 不是同类项,不能合并 C a·a·a=a3 √ D a6 ÷a2 =a4 3.D 4.C 【解析】用科学记数法表示一个绝对值大于 0且 小于 1的数时,1≤a<10,∴a=7.7;n是负整数,n 的值等于原数左起第一个非零数前所有零的个数, 则 n=-6,∴数字0.0000077用科学记数法表示为 7. 7×10-6. 5.B 【解析】逐项分析如下: 选项 逐项分析 正误 A 从装有 10个黑球的不透明袋子中摸出 一个球,恰好是红球是不可能事件 B 抛掷一枚普通正方体骰子所得的点数 小于 7是必然事件 √ C 抛掷一枚普通硬币,正面朝上是随机 事件 D 从一副没有大小王的扑克牌中抽出一 张牌,恰好是方块是随机事件 6.A 【解析】组成的图案要既是轴对称图形又是中心 对称图形,方子的坐标为(1,3),圆子的坐标为(2, 3). 7.A 【解析】b2 -4ac=(-m)2 -4×1×(-1)=m2 + 4,∵m2≥0,∴m2 +4>0,∴方程有两个不相等的实 数根. 8.C 【解析】∵一次函数 y=-2x+1中,k=-2<0,b =1>0,∴一次函数图象经过第一、二、四象限,∴一 次函数 y=-2x+1的图象不经过第三象限. 9.B 【解析】如解图,过点 B作 BM⊥OA于点 M,由题 意可知,c=0,抛物线的对称轴为直线 x=- b 2a,∴ OM=b 2a,∵△AOB为等边三角形,∴∠OBM=30°, ∴BM= OM tan30°=槡3b 2a,∴点 B的坐标为(-b 2a,槡3b 2a), ∵点 B在抛物线上,∴将点 B坐标代入方程,得 a (-b 2a)2 +b(-b 2a)=槡3b 2a,解得 b 槡=-2 3. 第 9题解图 第 10题解图 10.B 【解析】如解图,连接 AE,BE,CE,过点 E作 EF ⊥BC于点 F,作 EH⊥AB于点 H,作 EG⊥AC于点 G,过点 A作 AI⊥BC于点 I,设 EF的长为 x,∵点 E 为△ABC的内心,∴EH=EG=EF=x,∴S△ABC =1 2 AB·EH+1 2BC·EH+1 2AC·EG=1 2(AB+BC+ AC)·EF=1 2×(7+6+5)·x=9x,S△ABC =1 2BC ×AI,∴AI=3x,∴EF AI=1 3,∵MN∥BC,∴△AMN∽ △ABC,∴MN BC=2 3,∴MN=4. 二、填空题 11.3 【解析】原式 =2+1=3. 12.5 【解析】∵这组数据的众数为 8,∴x=8,把这组 数据按照从小到大的顺序排列为 1,3,5,8,8,∴这 组数据的中位数为 5. 13.100 【解析】∵五边形的内角和为 180°×(5-2) =540°,∴∠E=540°-(∠A+∠B+∠C+∠D)= 540°-440°=100°. 14.6 【解析】由题意可得:2a-b=1,-a+5b=5,∴ 两式相加得 a+4b=6. 15. 槡3 3-π 2 【解析】如解图,连接 OA,∵PA为⊙O的 切线,∴△PAO为直角三角形,∵⊙O的半径为槡3, 点 B是线段 PO的中点,∴OA 槡= 3,PO 槡=2 3,∴ ∠APO=30°,∴∠AOP=60°,PA=OP×sin60°=2 槡3×槡3 2 =3,∴S阴影 =S△PAO -S扇形AOB =1 2 槡×3× 3- 60·π·(槡3)2 360 = 槡3 3-π 2 . 第 15题解图 第 16题解图 16.(0,3)或(0,1) 【解析】如解图,过点 C作 CD⊥y 轴于点 D,由旋转知,AB=BC,∠ABO+∠CBD= 90°,∵∠CBD+∠BCD=90°,∴∠ABO=∠BCD, ∵ 11 ∠AOB=∠BDC=90°,∴△AOB≌△BDC,∴BD= AO=4,设点 B的坐标为(0,b),∴CD=BO=b,∴ 点 C的坐标为(-b,b-4),∵点 C在反比例函数 y =3 x上,∴ -b·(b-4)=3,解得 b=1或 3,∴点 B 的坐标为(0,3)或(0,1). 三、解答题(共 86分) 17.解:解不等式①得:x≥ -2, 3分!!!!!!!! 解不等式②得:x<3. 6分!!!!!!!!!! 在数轴上表示如解图: 第 17题解图 ∴不等式组的解集是 -2≤x<3. 8分!!!!! 18.解:原式 =a2 -2a+1 a-2 ÷a2 -1 a2 +a 1分!!!!!!! =(a-1)2 a-2 ÷(a+1)(a-1) a(a+1) 4分!!!! =(a-1)2 a-2 · a(a+1) (a+1)(a-1) 5分!!!! =a(a-1) a-2 , 6分!!!!!!!!!! 当 a=-2时,原式 =-2×(-2-1) -2-2 =-3 2. 8分 !! !!!!!!!!!!!!!!!!!! 19.证明:方法一: ∵CD⊥AB,BE⊥AC, ∴∠BDC=∠CEB=90°. 2分!!!!!!!! ∵AB=AC, ∴∠ABC=∠ACB. 3分!!!!!!!!!!! 在△BCD和△CBE中, ∠BDC=∠CEB,∠DBC=∠ECB,BC=CB, ∴△BCD≌△CBE. 7分!!!!!!!!!!! ∴BD=CE. 8分!!!!!!!!!!!!!! 方法二:∵CD⊥AB,BE⊥AC, ∴∠CDA=∠BEA=90°. 2分!!!!!!!!! 在△ADC和△AEB中, ∠CDA=∠BEA,∠A=∠A,AC=AB, ∴△ADC≌△AEB. 6分!!!!!!!!!!! ∴AD=AE, ∴AB-AD=AC-AE, ∴BD=CE. 8分!!!!!!!!!!!!!! 20.解:设矩形的长为 x步,则宽为(60-x)步,依题意 得: 1分!!!!!!!!!!!!!!!!!! x(60-x)=864, 5分!!!!!!!!!!!! 整理得:x2 -60x+864=0. 解得:x=36或 x=24(不合题意,舍去), 7分!! ∴60-x=60-36=24(步). ∴36-24=12(步). 答:该矩形的长比宽多 12步. 8分!!!!!!! 21.解:(1)由折叠性质得:BC=CE. 1分!!!!! 在ABCD中,BC=AD,BC∥AD, ∴CE=AD, 2分!!!!!!!!!!!!!! 又 AD∥CE, ∴四边形 ACED是平行四边形. 3分!!!!!! ∵AC⊥BC, ∴∠ACE=90°. ∴四边形 ACED是矩形; 4分!!!!!!!!! (2)方法一:在矩形 ACED中,AC=DE=4,∠DEC= ∠ADE=90°. ∵∠ACE=90°,由折叠性质可知:B,C,E三点共线, ∴BE=BC+CE=3+3=6. 在 Rt△BED中,由勾股定理得:BD= 62 +4槡 2 =2 槡13. 5分!!!!!!!!!!!!!!!!! 在 Rt△ABC中,同理可得:AB=5. 如解图①,过点 A作 AF⊥BD于点 F, ∴S△ABD =1 2BD·AF=1 2AD·DE, ∴ 1 2 槡×2 13·AF=1 2×3×4,AF= 槡6 13 13 . 6分 !! !!!!!!!!!!!!!!!!!! 在 Rt△AFB中,sin∠ABD=AF AB= 槡6 13 13 5 = 槡6 13 65 . 8分!!!!!!!!!!!!!!!!!! 方法二:由(1)得∠BED=∠ACB=90°,DE=AC= 4,CE=BC=3, 在 Rt△BED中,由勾股定理得:BD= BE2 +DE槡 2 = 62 +4槡 2 槡=2 13, 在 Rt△ABC中,同理可得:AB=5. 在ABCD中,AO=1 2AC=1 2×4=2,BO=1 2BD= 1 2 槡 槡×2 13= 13. 5分!!!!!!!!!!! 如解 图 ②,过 点 O作 OF⊥ AB于 点 F,则 ∠OFA =90°. ∵∠OAF=∠BAC,∠OFA=∠BCA=90°, ∴△OAF∽△BAC, ∴OF BC=OA BA,即OF 3 =2 5,∴OF=6 5, 6分!!!! 在 Rt△OFB中,sin∠ABD=OF OB= 6 5 槡13 = 槡6 13 65 . 8分 ! !!!!!!!!!!!!!!!!!! 第 21题解图① 第 21题解图② 21 22.解:(1)3 10; 3分!!!!!!!!!!!!!! (2)甲 店 每 售 出 一 台 电 脑 的 平 均 利 润 值 为: 160×20+200×15+240×10+320×5 50 =204(元), 乙 店 每 售 出 一 台 电 脑 的 平 均 利 润 值 为: 160×8+200×10+240×14+320×18 50 =248(元), 9分!!!!!!!!!!!!!!!!!! ∵248>204, 即乙店每售出一台电脑的平均利润大于甲店, 又∵两店每月电脑的总销量相等, ∴应对甲店作出暂停营业的决定. 10分!!!! 23.解:(1)将点(n,3n)和(n+1,2n)代入 y=k x得:3n =k n,2n= k n+1, 1分!!!!!!!!!!!! ∴3n2 =2n(n+1), 2分!!!!!!!!!!! 解得 n=2或 n=0(舍去), ∴n=2; 3分!!!!!!!!!!!!!!!! (2)由(1)得:点(2,6)在反比例函数 y=k x(k>0,x >0)的图象上, 将点(2,6)代入 y=k x,得 k=12. ∴反比例函数解析式为 y=12 x. 4分!!!!!! 设 OC=a,点 B在直线 y=x,∴点 B(a,a). 又∵BC⊥x轴,∴△BOC为等腰直角三角形. ∵AB⊥l,AD⊥BC, ∴△ABD为等腰直角三角形. 6分!!!!!! 设 BD=b,则 AD=b, ∴点 A(a+b,a-b). 将点 A(a+b,a-b)代入 y=12 x,得 a-b= 12 a+b, 即 a2 -b2 =12, 8分!!!!!!!!!!!!! 又 S1 =1 2a2,S2 =1 2b2, ∴S1 -S2 =1 2(a2 -b2)=1 2×12=6. 10分!!! 24.解:(1)如解图①,⊙F为所求作的圆; 3分!!! 第 24题解图① (2)①证明: 方法一:如解图②,连接 AF. ∵四边形 ABCD为菱形,∴AC⊥BD. ∴∠DBC=90°-∠ACB. 4分!!!!!!!!! ∵FA=FE,∴∠AEF=∠FAE, ∴∠AEF=1 2(180°-∠AFE)=90°-1 2∠AFE. 5分!!!!!!!!!!!!!!!!!! 又∠ACB=1 2∠AFE, ∴∠AEF=90°-∠ACB, 7分!!!!!!!!! 又∵∠DBC=90°-∠ACB, ∴∠AEF=∠DBC; 8分!!!!!!!!!!! 第 24题解图② 方法二:如解图②,连接 AF, 在菱形 ABCD中,CB=CD,AC 平分∠BCD, ∴∠BCD=2∠ACB. 4分! 又∠AFE=2∠ACE, ∴∠BCD=∠AFE. 5分!!!!!!!!!!! 在等腰三角形 CBD中,∠DBC=180°-∠BCD 2 , 在等腰三角形 FEA中,∠AEF=180°-∠AFE 2 , 7分 ! !!!!!!!!!!!!!!!!!! ∴∠AEF=∠DBC; 8分!!!!!!!!!!! ②方法一: ∵四边形 ABCD为菱形, ∴∠ABD=∠CBD,AO=OC,BO=DO=1 2BD=1 2 槡 槡×6 3=3 3. 9分!!!!!!!!!!!!! 在 Rt△ABO中,AO= AB2 -BO槡 2 = 62 -( 槡3 3)槡 2 =3. 又∵∠AGB=∠FGE,∠ABG=∠FEG, ∴△ABG∽△FEG, ∴AG FG=BG EG, ∴AG·GE=GF·BG. 10分!!!!!!!!! ∵∠GEF=∠FBE,∠GFE=∠EFB, ∴△EFB∽△GFE, ∴EF GF=BF EF, ∴GF·BF=EF2, 11分!!!!!!!!!!! ∴t=GF2 +AG·GE=GF2 +GF·BG=GF(GF+ BG)=GF·BF=EF2. 在菱形 ABCD中,AC⊥BD,EF=AF≥AO, ∴EF2≥AO2 =32 =9. 第 24题解图③ 如解图③,当点 F与点 O重 合时,AF最小. ∴当 EF=AO=3时,t的最 小值为 9. 12分 !!!! 31 如解图③,当点 E与点 B重合时,AF最大. 由题意可知:AF=BF,设 AF=x,则 OF 槡=3 3-x, 由勾股定理得:AO2 +OF2 =AF2,即 32 +( 槡3 3-x)2 =x2, 解得:x 槡=2 3. ∴当 x 槡=2 3时,t的最大值为 12, ∴9≤t≤12. 13分!!!!!!!!!!!!! 第 24题解图④ 方法二:如解图④,设⊙F的 半径为 r,连接 EQ,AP,AF. 在菱形 ABCD中,AC⊥BD, 则 AF≥OA,即 r≥3. ∵ ) AQ = ) AQ, ∴ ∠QEG =∠APG. 又∵∠QGE=∠PGA, ∴△QEG∽△APG, 10分!!!!!!!!!! ∴EG PG=QG AG,即 EG·AG=PG·QG. 11分!!!! ∴t=GF2 +AG·GE=GF2 +PG·QG=GF2 +(r- GF)·(r+GF)=GF2 +r2GF=r2 =AF2. 如解图④,当点 F与点 O重合时,AF最小. ∴当 r=3时,t的最小值为 9. 12分!!!!!! (以下同法一) 25.解:(1)把点 B(3,0)代入 y=x2 +bx-3,得:b= -2, ∴二次函数的表达式为:y=x2 -2x-3; 2分!! (2)①∠DMT为定值. 3分!!!!!!!!!! 理由如下:如解图①,连接 AD, 第 25题解图① ∵抛物线 y=x2 -2x-3 =(x-1)2 -4, ∴抛物线的对称轴为直线 x =1. 又点 D的纵坐标为 槡2 3, ∴D(1, 槡2 3). 4分!!! 在 y=x2 -2x-3中,令 y= 0,则 x2 -2x-3=0, 解得:x1 =-1,x2 =3, ∴A(-1,0). 在 Rt△AED中,tan∠DAE=DE AE= 槡2 3 2 槡= 3, 5分 !!! !!!!!!!!!!!!!!!!!! ∴∠DAE=60°, ∴∠DMT=2∠DAE=120°, ∴在点 T的运动过程中,∠DMT为定值 120°; 6分 ! !!!!!!!!!!!!!!!!!! ②方法一:如解图②, ∵MT=1 2AD,又 MT=MD, 第 25题解图② ∴MD=1 2AD, ∴△ADT的 外 接 圆 圆 心 M 在 AD的中垂线上, ∴点 M是线段 AD的中点, 此时 AD为⊙M的直径,MD =1 2AD. 7分!!!!!! ∵A(-1,0),D(1, 槡2 3), ∴点 M的坐标为(0,槡3). 8分!!!!!!!! 方法二:如解图③, ∵A(-1,0),D(1, 槡2 3), ∴线段 AD的中点 P的坐标为(0,槡3),AD=4. 由题意得:圆心 M在 AD的中垂线上,设直线 MP交 x轴于点 Q. ∴PQ⊥AD,即∠APQ=90°,又∠DAQ=60°, ∴∠PQA=30°. 在 Rt△OPQ中,OP 槡= 3,OQ= OP tan30°=3,即 Q(3, 0), 第 25题解图③ ∴Q与点 B重合. 由 P(0,槡3)、Q(3,0)可求得 直线 MP的表达式为 y=- 槡3 3x 槡+ 3. 7分!!!!! 设点 M(m,-槡3 3m 槡+ 3),作 MH⊥x轴于点 H,则 HT=m+1, T(2m+1,0). ∵MT=1 2AD,∴MT=1 2AD =1 2×4=2. 在 Rt△MHT中,由勾股定理,得:MH2 +HT2 =MT2 ∴(-槡3 3m 槡+ 3)2 +(m+1)2 =22,解得:m=0. ∴M(0,槡3). 8分!!!!!!!!!!!!!! (3)如解图④,作 MH⊥x轴于点 H,则 AH=HT= 1 2AT, 又 HT=a,∴H(a-1,0)、T(2a-1,0) 9分!!! ∵OH≤x≤OT,动点 T在射线 EB上运动, ∴0≤a-1≤2a-1, ∴a≥1,∴2a-1≥1. 10分!!!!!!!!!! (ⅰ)当 2a-1≥1 1-(a-1)≥2a{ -1-1,即 1≤a≤ 4 3时, 当 x=a-1时,ymax =(a-1)2 -2(a-1)-3=a2 -4a ; 41 当 x=1时,ymin=-4. 11分!!!!!!!!! (ⅱ)当 0<a-1≤1 2a-1>1 1-(a-1)<2a{ -1-1 ,即 4 3<a≤2时, 当 x=2a-1时,ymax=(2a-1)2 -2(2a-1)-3= 4a2 -8a;当 x=1时,ymin=-4. 12分!!!!! (ⅲ)当 a-1>1,即 a>2时, 当 x=2a-1时,ymax=(2a-1)2 -2(2a-1)-3= 4a2 -8a. 当 x=a-1时,ymin =(a-1)2 -2(a-1)-3=a2 -4a. 综上所述,当 1≤a≤ 4 3时,y的最大值为 a2 -4a,最 小值为 -4;当 4 3<a≤2时,y的最大值为 4a2 -8a, 最小值为 -4;当 a>2时,y的最大值为 4a2 -8a,最 小值为 a2 -4a. 13分!!!!!!!!!!!! 第 25题解图④ 51 2019年初中漳州市质量检测数学试卷参考答案及评分建议 一、选择题(本大题共 10小题,每小题 4分,共 40分) 1.D 2.B 【解析】用科学记数法将一个绝对值大于 10的数 表示为 a×10n的形式,其中 1≤ |a|<10,故 a=1.6,n 为正整数,n的值为原数的整数位减 1,因此 n=7-1 =6,故 1600000用科学记数法表示为 1.6×106. 3.A 4.C 【解析】圆锥的主视图是三角形,圆柱的主视图是 矩形,球的主视图是圆,正方体的主视图是正方形,故 主视图不可能是多边形的是球. 5.A 【解析】∵AB∥CD∥EF,∴AC CE=BD DF.∵AC=4,CE =6,BD=3,∴ 4 6= 3 DF,解得 DF=4.5,即 DF的值是 4.5. 6.D 【解析】由题图可知,a<b<c,∵a+b=0,∴实数 a与 b互为相反数,a<0,b>0,c>0,abc<0,则结论 错误的是 D选项. 第 7题解图 7.B 【解析】如解图,过点 A作 AG ⊥BF于点 G,设正六边形的边长 为 a,∵六边形 ABCDEF是正六边 形,∴AB=AF=BC=a,∠BAG= ∠FAG=1 2∠FAB=60°.∴FG= AF×sin60°=槡3 2a.∵AG⊥BF,∴BF=2FG 槡= 3a.∴ S△BCF =1 2×a 槡× 3a=槡3 2a2,S正六边形ABCDEF =1 2×a×槡3 2a ×6= 槡3 3 2 a2.∴飞镖落在阴影部分的概率为 槡3 2a2 槡3 3 2 a2 =1 3. 8.C 【解析】A选项为正比例函数,∵ 1 2>0,∴对于任 意实数 x,y随 x的增大而增大,不符合题意;B选项为 反比例函数,∵2>0,∴在 x≠0的情况下,y随 x的增 大而减小,不符合题意;C选项为一次函数,-1<0, ∴对于任意实数 x,y随 x的增大而减小,符合题意;D 选项为二次函数,对称轴为 y轴且函数图象开口向 上,∴当 x≥0时,y随 x的增大而增大,当 x≤0时,y 随 x的增大而减小,不符合题意. 9.B 【解析】∵x=2是关于 x的一元一次方程的解,代 入得 2a-2=b,∴b-2a=-2.∴3b-6a+2=3(b- 2a)+2=-6+2=-4. 10.D 【解析】∵四边形 ABCD是正方形,∴AC⊥BD.∴ 第 10题解图 ∠AOF=90°.∵BH⊥AE,∴∠BGF =90°.∵∠AFO=∠BFG,∴△AOF ∽△BGF.故 ② 正 确;∴ ∠OAF= ∠FBG.∵ OA=OB,∴ △AOF≌ △BOH(ASA).∴OF=OH.故①正 确;∵ ∠GAH =∠OBH,∠AGH = ∠BOH=90°,∴ △AGH∽ △BOH.∴ AH GH =BH OH.∵ ∠AHB=∠GHO,∴ △ABH∽ △GOH.∴ ∠ABH = ∠GOH.又∵tan∠ABH=tan∠BEA=AB BE=2,∴tan ∠GOH=2.故③正确;如解图,作 OQ⊥AE交 AE于 点 Q,由③知∠GOH=∠ABH,∵∠GOH=∠GAO+ ∠AGO,∠ABH =∠ABO +∠DBH,又 ∵ ∠OBH = ∠GAH,∴∠FGO=∠ABO=45°.作 OM⊥BH于点 M,∴GQ=槡2 2OG.∵OQ=QG,∠AQO=∠AGH=90°, ∴四边形 QOMG为正方形.∴ QO=OM,∠OQF= ∠OMH=90°,∵OF=OH,∴△QOF≌△MOH(HL). ∴QF=MH,即 2GQ 槡= 2OG=GM+GQ=FG+FQ+ GM=FG+GM+HM=FG+GH. 二、填空题(本大题共 6小题,每小题 4分,共 24分) 11.1 12.5 【解析】∵直角三角形两直角边长为 6和 8,∴斜 边长为 62 +8槡 2 =10,斜边上的中线长为斜边的一 半.则此直角三角形斜边上的中线长为 5. 13.1 2 【解析】由题意得1+2+3+x 4 =2,解得 x=2,则 这 组 数 据 的 方 差 为 (1-2)2 +(2-2)2 +(3-2)2 +(2-2)2 4 =1 2. 14.槡2 2 【解析】∵⊙O是△ABC的外接圆,∠A=45°, ∴∠BOC=90°.∵OB=OC,∴∠OCB=45°.则 cos ∠OCB=槡2 2. 15.2 【解析】由题意得 m+n=-2,mn=-1,∴m2n+ mn2 =mn(m+n)=(-2)×(-1)=2. 第 16题解图 16.12 【解析】∵四边形 OABC 是矩 形,∴ OA=CB,AB= OC.∵ △DEF与 △DEB关 于直 线 DE对 称,∴ BE= EF.∵ 点 B的 坐 标 为 (8, 4),点 D,E在反比例函数 y =k x(k>0)上,∴D(k 4,4),E(8,k 8).∴EF=BE = 61 4-k 8,AE=k 8,设直线 DE的解析式为 y=mx+n, 代入 D,E坐标,得 4=k 4m+n k 8=8m+{ n ,解得 m=-1 2 n=4+k{ 8 ,∴ 直线 DE为 y=-1 2x+4+k 8.如解图,连接 BF,设 直线 BF的解析式为 y=2x+q,代入点 B(8,4),得 4 =16+q,∴q=-12.直线 BF的解析式为 y=2x- 12,令 y=0,解得 x=6,∴F(6,0),∴AF=2,在 Rt △AEF中,∵AE2 +AF2 =EF2,∴(k 8)2 +22 =(4- k 8)2,解得 k=12. 三、解答题(本大题共 9小题,共 86分.请在答题卡的相 应位置解答) 17.解:由①得:x≥3, 2分!!!!!!!!!!!! 由②得:x<4, 4分!!!!!!!!!!!!!! ∴原不等式组的解集为:3≤x<4. 6分!!!!! 不等式组的解集表示在数轴上如解图, 第 17题解图 8分!!!!!!!! 18.解:原式 =(a-b)2 a · a (a+b)(a-b) 4分!!!! =a-b a+b, 6分!!!!!!!!!!!! 当 a 槡= 2-1,b=1时, 原式 =(槡2-1)-1 (槡2-1)+1 7分!!!!!!!!!!! =槡2-2 槡2 槡=1- 2. 8分!!!!!!!!!! 19.解:作图如解图; 2分!!!!!!!!!!!! 第 19题解图 已知:在△ABC中,AB=AC,BD、CE是△ABC的角平 分线. 求证:BD=CE. 4分!!!!!!!!!!!!! 证明:方法一: ∵AB=AC, ∴∠ABC=∠ACB. 5分!!!!!!!!!!! ∵BD、CE是△ABC的角平分线, ∴∠CBD=1 2∠ABC,∠ECB=1 2∠ACB, ∴∠CBD=∠ECB. 6分!!!!!!!!!!! ∵BC是公共边, ∴△BCD≌△CBE(ASA) 7分!!!!!!!!! ∴BD=CE. 8分!!!!!!!!!!!!!! 方法二: ∵AB=AC, ∴∠ABC=∠ACB. 5分!!!!!!!!!!! ∵BD、CE是△ABC的角平分线, ∴∠ABD=1 2∠ABC,∠ACE=1 2∠ACB, ∴∠ABD=∠ACE. 6分!!!!!!!!!!! ∵∠A是公共角, ∴△ABD≌△ACE(ASA), 7分!!!!!!!! ∴BD=CE. 8分!!!!!!!!!!!!!! 20.解:方法一: 设该店有客房 x间, 1分!!!!!!!!!!! 依题意得:7x+7=9(x-1) 4分!!!!!!!! 解得 x=8. 6分!!!!!!!!!!!!!!! ∴7x+7=56+7=63. 7分!!!!!!!!!! 答:该店有客房 8间,房客 63人. 8分!!!!!! 方法二: 设该店有客房 x间,房客有 y人, 1分!!!!!! 依题意得: y=7x+7, y=9(x-1{ ), 4分!!!!!!!!! 解得: x=8, y=63{ , 7分!!!!!!!!!!!!! 答:该店有客房 8间,房客 63人. 8分!!!!!! 21.解:(1)调查人数 = 10 25% =40(人), 2分!!!!! 10+11+4x+9+3y=40, 4分!!!!!!!!! ∵x、y是满足 x<y的正整数, ∴x=1,y=2; 6分!!!!!!!!!!!!!! (2)“最想去华安官畲村”的学生人数 =11 40×1200= 330(人). 7分!!!!!!!!!!!!!!! 答:“最想去华安宫畲村”的学生人数约为 330人. 8分!!!!!!!!!!!!!!!!!! 22.(1)解:方法一:如解图①所示; 第 22题解图① 3分!!!!!!!! ∴△DEF就是所求作的三角形. 4分!!!!!! 方法二:如解图②所示; 第 22题解图② 3分 !!!!!!!! 71 ∴△DEF就是所求作的三角形. 4分!!!!!! 方法三:如解图③所示; 第 22题解图③ 3分!!!!!!!! ∴△DEF就是所求作的三角形. 4分!!!!!! 第 22题解图④ (2)解:∵AB 槡= 3,AC= 槡6,BC=3, ∴AB2 +AC2 =BC2, ∴∠BAC=90°. 5分 !! !!!!!! ∵△ABC平移得△DEF, ∴S△DEF =S△ABC =1 2·槡3·槡6=3 2槡2. 6分!!!! ∵EF=BC=3且 BE=2, ∴EC=BC-BE=1. 7分!!!!!!!!!!! ∵∠DFE=∠ACE,∠DEF是公共角, ∴△ECH∽△EFD. 8分!!!!!!!!!!! ∴S△ECH S△EFD =(EC EF) 2 =1 9. 9分!!!!!!!!!! ∴S四边形DHCF =8 9S△DEF =8 9· 3 2槡2=4 3槡2. 10分! 23.(1)证明:如解图,连接 OC. 1分!!!!!!!! ∵AB是⊙O的直径, 第 23题解图 ∴ ∠ACB=90°,即 ∠ACO + ∠BCO=90°. 2分!!!! ∵OB=OC, ∴∠B=∠BCO, 3分!!! ∴∠ACO+∠B=90°. ∵∠ECD=∠B, ∴∠ECD+∠ACO=90°,即∠OCE=90°. 4分!! 又∵OC为⊙O的半径, ∴EC是⊙O的切线. 5分!!!!!!!!!!! (2)解:方法一:∵OA=3, ∴AB=6. 6分!!!!!!!!!!!!!!! ∵OD⊥AB,∠ACB=90°, ∴∠AOD=∠ACB=90°. ∴∠A是公共角, ∴△ABC∽△ADO. 7分!!!!!!!!!!! ∴AD AB=AO AC. 8分!!!!!!!!!!!!!!! ∴CD+2 6 =3 2. 9分!!!!!!!!!!!!! ∴CD=7. 10分!!!!!!!!!!!!!!! 方法二:∵OA=3, ∴AB=6. 6分!!!!!!!!!!!!!!! ∵∠BCA=90°,AC=2, ∴cosA=AC AB=2 6=1 3. 7分!!!!!!!!!! ∵OD⊥AB, ∴cosA=OA AD= 3 CD+2. 8分!!!!!!!!!! ∴ 3 CD+2=1 3. 9分!!!!!!!!!!!!! ∴CD=7. 10分!!!!!!!!!!!!!!! 24.(1)证明:方法一:由折叠可知 AB=AF,BE=EF, ∠BAE=∠FAE. 1分!!!!!!!!!!!! ∵四边形 ABCD是平行四边形, ∴AD//BC, ∴∠FAE=∠AEB, ∴∠BAE=∠AEB, 2分!!!!!!!!!!! ∴AB=BE, ∴AB=BE=EF=AF. 3分!!!!!!!!!! ∴四边形 ABEF是菱形; 4分!!!!!!!!! 方法 二:由 折 叠 可 知 ∠BAE =∠DAE,∠AEB = ∠AEF,AB=AF. 1分!!!!!!!!!!!! ∵四边形 ABCD是平行四边形, ∴AD//BC, ∴∠FAE=∠AEB, ∴∠BAE=∠AEF, 2分!!!!!!!!!!! ∴AB∥EF ∴四边形 ABEF是平行四边形. 3分!!!!!! ∵AB=AF, ∴四边形 ABEF是菱形. 4分!!!!!!!!! (2)解:方法一:①如解图①所示,当点 M在线段 BE 上时,在射线 MC上取点 G,使 MG=AB,连接 GN、 EN. 5分!!!!!!!!!!!!!!!!!! 第 24题解图① ∵∠AMN=∠B=α, ∠AMN+∠2=∠1+∠B, ∴∠1=∠2. 6分!!!! ∵AM=NM,AB=MG, ∴△ABM≌△MGN(SAS), 7分!!!!!!!! ∴∠B=∠3,NG=BM. ∵MG=AB=EB, ∴EG=BM=NG, ∴∠4=∠ENG=1 2(180°-α)=90°-1 2α. 8分 !!! !!!!!!!!!!!!!!!!!! ∵四边形 ABEF是菱形, 第 24题解图② ∴AB//EF, ∴∠FEC=∠B=α, ∴∠FEN=∠FEC-∠ 4= 81 α-(90°-1 2α)=3 2α-90°. 9分!!!!!!! ②如解图②所示,当点 M在线段 EC上时,在 BC的 延长线上截取 MG=AB,连接 GN、EN. 10分!!! 同理可证,∠FEN=∠FEC-∠4=α-(90°-1 2α) =3 2α-90°. 11分!!!!!!!!!!!!! 综上所述,∠FEN=3 2α-90°. ∴当点 M在 BC上运动时, 点 N在射线 EH上运动(如解图③) 第 24题解图③ ∴当 FN⊥EH时,FN最小. FN最小值 =FE· sin(3 2α- 90°)=6sin(3 2α-90°). 12分!!!!!!! 方法二:①如解图④所示,当点 M在线段 BE上时, 在 AB上取点 G,使 AG=ME,连接 GM、EN. 5分! 第 24题解图④ ∵∠AMN=∠B=α,∠AMN +∠2=∠1+∠B, ∴∠1=∠2. 6分!!!! ∵AM=NM,AG=ME, ∴△AGM≌△MEN(SAS), 7分!!!!!!!! ∴∠MEN=∠AGM, ∴∠3=∠4. ∵AG=ME,AB=EB, ∴BG=BM, ∴∠3=∠BMG=1 2(180°-α)=90°-1 2α=∠4. 8分!!!!!!!!!!!!!!!!!! ∵四边形 ABEF是菱形, ∴AB∥EF, ∴∠FEC=∠B=α, ∴∠FEN=∠FEC-∠4=α-(90°-1 2α)=3 2α- 90°. 9分!!!!!!!!!!!!!!!!!! ②如解图⑤所示,当 M点在线段 EC上时,在 BA延 第 24题解图⑤ 长线上截取 AG=ME,连接 GM、EN. 10分!!!!! 同理可证,∠FEN=∠FEC -∠4=α-(90°-1 2α)= 3 2α-90°. 11分!!!! 综上所述,∠FEN=3 2α-90° ∴当点 M在 BC上运动时,点 N在射线 EH上运动 (如解图⑥) 第 24题解图⑥ ∴当 FN⊥EH时,FN最小. FN最小值 =FE· sin(3 2α- 90°)=6sin(3 2α-90°). 12分 ! !!!!!!! 25.(1)解:∵抛物线与 y轴交于点(0,-3), ∴ -2m=-3. 1分!!!!!!!!!!!!! 解得 m=3 2. 2分!!!!!!!!!!!!!! ∴抛物线解析式为 y=x2 +2x-3=(x+1)2 -4. 3分 ! !!!!!!!!!!!!!!!!!! ∴抛物线的顶点坐标为(-1,-4); 4分!!!! (2)证明:∵ y=x2 +(2m-1)x-2m, y=(k-1)x+2m-k+2{ , ∴x2 +(2m-1)x-2m=(k-1)x+2m-k+2. ∴x2 +(2m-k)x-4m+k-2=0. 5分!!!!! ∴Δ=(2m-k)2 -4(-4m+k-2) =(2m-k)2 +16m-4k+8 =(2m-k)2 +4(2m-k)+4+8m+4 =(2m-k+2)2 +8m+4. 7分!!!!!!! ∵ m>-1 2,(2m-k+2)2≥0, 8分!!!!!! ∴Δ>0. 9分!!!!!!!!!!!!!!!! ∴抛物线与直线 l必有两个交点; (3)解:依题意可知 y最小值 =-4. 即4×1×(-2m)-(2m-1)2 4 =-4,解得 m=3 2或 m=-5 2. ∵ -1 2<m≤ 3 2, ∴m=3 2,此时抛物线的对称轴为直线 x=-1. 10分 ! !!!!!!!!!!!!!!!!! ①当 k≤ -1时,抛物线在 k-2≤x≤k上,y随 x增 大而减小,此时 y最小值 =k2 +2k-3. ∴ k2 +2k-3=2k+1. 解得 k1 =2>-1(舍去),k2 =-2. 11分!!!! ②当 k-2<-1<k,即 -1<k<1时,抛物线在 k-2 ≤x≤k上,y最小值 =-4. ∴ 2k+1=-4. ∴解得 k=-5 2<-1(舍去). 12分!!!!!! ③当 k-2≥ -1,即 k≥1时,抛物线在 k-2≤x≤k 上,y随 x增大而增大 , 91 此时 y最小值 =(k-2)2 +2(k-2)-3. ∴(k-2)2 +2(k-2)-3=2k+1. ∴解得 k1 槡=2+2 2,k2 槡=2-2 2<1(舍去). 13分 !! !!!!!!!!!!!!!!!!! 综上所述,直线 l的解析式为 y=-3x+7或 y=(1 槡+2 2)x 槡+3-2 2. 14分 !!!!!!!!!!! 02 2019年莆田市初中毕业班质量检查试卷 数学参考答案及评分标准 一、选择题:本大题共 10小题,每小题 4分,共 40分.在 每小题给出的四个选项中,只有 一项 是符 合题目 要 求的. 1.D 【解析】∵ |-3|=3,-2<-1<0<3,∴这四个 数中,最大的数是 |-3|. 2.C 【解析】选项 A的俯视图是带圆心的圆,选项 B 的俯视图是矩形,选项 C的俯视图是三角形,选项 D 的俯视图是矩形,故选 C. 3.A 【解析】逐项分析如下: 选项 逐项分析 正误 A 22 ÷25 =22-5 =2-3 √ B 25 ÷22 =25-2 =23 C 22 ×25 =27 D (-2)×(-2)×(-2)=-23 4.A 【解析】由图 可 得,∠CDE=40°,∠C=90°,∴ ∠CED=90°-40°=50°.又∵DE∥AF,∴∠CAF= 50°,∵∠BAC=60°,∴ ∠BAF=60°-50°=10°,故 选 A. 5.D 【解析】∵ 3槡 2 槡= 9=3, 槡 槡2< 8=2 2<3, 槡3<2 3 槡= 12<4,槡 槡 槡 槡 槡16< 4+ 5=2+ 5< 25,∴k的可能 值是槡 槡4+ 5. 6.C 【解析】根据已知可得,点 E(m,n)向右平移一个 单位长度,再向下平移一个单位长度可得点(m+1,n -1),则在平面直角坐标系中对应的点可能是 C点. 7.A 【解 析 】由 题 意 可 得,原 数 据 的 平 均 数 为 180+184+188+190+192+194 6 =188,原 数据的 中 位 数 为 188+190 2 = 189;新 数 据 的 平 均 数 为 180+184+188+190+186+194 6 =187,新 数据的 中 位数为188+186 2 =187;∴与换人前相比,场上队员的 身高平均数变小,中位数变小,故选 A. 8.B 【解析】设过(-2,0),(0,3)的直线解析式为 y= 第 9题解图 kx+b,则 -2k+b=0, b=3{ , 解 得 k=3 2, b=3{ , ∴直线解析式为 y= 3 2x+3.当 x=-3时,y=-3 2,此时点(-3,-3 2) 在第三象限,不符合题意;当 x=3时,y=15 2,此时点 (3,15 2)在第一象限,符合题意;当 y=-3时,x=-4, 此时点(-4,-3)在第三象限,不符合题意;当 y=3 时,x=0,此时点(0,3)在 y轴上,不符合题意;故 选 B. 9.B 【解析】如解图,连接 OB,OC,∵AB,AC均为⊙O 的切线,∴∠ABO=∠ACO=90°,∴∠A+∠BOC= 360°-(∠ABO+∠ACO)=360°-180°=180°.又∵ ∠BOC=2∠D,∴∠A+2∠D=180°,故选 B. 10.C 【解 析 】依 题 意 得 0.7=9a+3b+c, 0.8=16a+4b+c, 0.5=25a+5b+c{ , 解 得 a=-0.2, b=1.5, c=-2{ , ∴p=-0.2t2 +1.5t-2= -0.2(t- 3.75)2 +0.8125,即当 t=3.75时,p有最大值.即最 佳加工时间为 3.75分钟. 二、填空题:本大题共 6小题,每小题 4分,共 24分. 11.3.1×104 12.x=2 y{ =0 【解析】 x-y=2①, 2x+y=4②{ ,① +②,得 3x=6,解 得 x=2,把 x=2代入①,得 2-y=2,解得 y=0,∴ 原方程组的解是 x=2, y=0{ . 13.6 【解析】∵DE是 BC的垂直平分线,∴BD=CD, 则△ACD的周长 =AC+AD+CD= AC+AD+BD= AC+AB=6. 14.2 3 【解析】画树状图如解图, 第 14题解图 由树状图可得共有 6种等可能的情况,其中摸出的 两个球中有白球的情况有 4种,∴P(摸到的球两个 球中有白球)=4 6=2 3. 第 16题解图 15.3r2 【解析】如解图,连接 AD, CD,AC,AG,根据已知作出第一 个等分点 H,连接 AH,BH,CH, BC,BO,OC,∵A,B,C,D,E,F六 个等分点,∴ 每 条 弧 的 度 数 是 60°.∵AD是⊙O直径,∴∠ACD =90°,在 Rt△ACD中,AD=2r , 12 ∠DAC=30°,∴AC 槡= 3r.∵DG=AG=CA,OD=OA, ∴OG⊥AD.∴∠GOA=90°.∴OG= AC2 -OA槡 2 = (槡3r)2 -r槡 2 槡= 2r.∴AH=OG 槡= 2r,AH2 =2r2.又∵ OA2 +OH2 =2r2,∴ OA2 +OH2 = AH2,∴ ∠AOH= 90°.∴ ) BH的度数是 90°-60°=30°,∴H是 ) BC的中 点,同理,其它点是另外 5条弧的中点,∴顺次连接 这些等分点构成的多边形是正十二边形.∴BC⊥ OH.∴顺次连接这些等分点构成的多边形面积是: 1 2BC·OH×6=1 2r·r×6=3r2. 第 16题解图 16.24 【解析】如解图,过 A,B 作 x轴和 y轴的垂线,交于 D,得到矩形 OCDE,设 P(a, 2 a),当 x=a时,y=10 a;当 y =2 a时,2 a=10 x,x=5a,∴A (5a,2 a),D(5a,10 a),B(a,10 a),则 BD=4a,AD=10 a -2 a=8 a,∴S△ABO =S矩形OCDE -S△ABD -S△AOC -S△OBE =5a×10 a -1 2 ×4a×8 a-10 2 -10 2 =50-16-5-5 =24. 三、解答题:本大题共 9小题,共 86分.解答应写出必要 的文字说明、证明过程、正确作图或演算步骤. 17.解:原式 =1-2+1 2 6分!!!!!!!!!!! =-1 2. 8分!!!!!!!!!!!! 18.已知:如解图,OC是∠AOB的平分线,P是 OC上一 点,PE⊥OA,PF⊥OB,垂足分别为 E、F. 求证:PE=PF. 2分!!!!!!!!!!!!! 第 18题解图 4分!!!!!!!!!!!!!!!!!!! 证明:∵OC是∠AOB的平分线, ∴∠POE=∠POF. ∵PE⊥OA,PF⊥OB, ∴∠PEO=∠PFO. 6分!!!!!!!!!!! 又∵OP=OP, ∴△POE≌△POF(AAS). ∴PE=PF. 8分!!!!!!!!!!!!!! 19.解:原式 =1-m m · m (1+m)(1-m) 4分!!!!! = 1 m+1, 6分!!!!!!!!!!!! 当 m=2时, 1 m+1=1 3. 8分!!!!!!!!! 20.解:(1)如解图,点 F为所求作的点. 4分!!!! 第 20题解图 (2)△ADE和 △FCE;旋转中心为点 E,旋转角为 100°. 8分!!!!!!!!!!!!!!!!! 21.解:(1)17,20; 4分!!!!!!!!!!!!! (2)扇形统计图中“3次”所对应扇形的圆心角的度 数为 360°×20% =72°; 6分!!!!!!!!! (3)估计该小区居民在一周内前往“木兰溪左岸绿 道”锻炼“4次及以上”的人数 为 2000×3 50=120人. 8分!!!!!!!!!! 22.(1)证明:∵AC⊥BD,∴∠BEC=90°,∴∠CBD+ ∠BCA=90°, 2分!!!!!!!!!!!!!! ∵∠AOB=2∠BCA,∠COD=2∠CBD, ∴∠AOB+∠COD=2(∠BCA+∠CBD)=180°; 4分 ! !!!!!!!!!!!!!!!!!! 第 22题解图 (2)解:如解图,延长 BO交⊙O 于点 F,连接 AF. 5分!!! 则∠AOB+∠AOF=180°, 又由 (1)得:∠AOB+∠COD =180°, ∴∠AOF=∠COD. ∴AF=CD=6. 8分!!!! ∵BF为⊙O的直径, ∴∠BAF=90°,在 Rt△ABF中,BF= 62 +8槡 2 =10. ∴⊙O的直径为 10. 10分!!!!!!!!!! 23.解:(1)如解图①,以点 B为原点,BC所在的直线为 x轴,建立平面直角坐标系,则点 A(0,5),E(5,3),C (13,0), 1分!!!!!!!!!!!!!!!! 第 23题解图① 方法一:可得直线 AC:y=-5 13x+5, 4分!!!! 当 x=5时,y=-5 13×5+5=40 13≠3,故点 E不在直 线 AC上, 因此 A、E、C三点不共线. 同理 A、G、C三点不共线, 所以拼合的长方形内部有 22 空隙,故面积多了 1cm2; 5分!!!!!!!!! 方法二:可得 AC= 132 +5槡 2 槡= 194,AE= 52 +2槡 2 槡= 29,CE= 82 +3槡 2 槡= 73, 4分!!!!!! 由于 AE+EC≠AC,故点 E不在 AC上, 因此 A、E、C三点不共线. 同理 A、G、C三点不共线,所以拼合的长方形内部有 空隙,故面积多了 1cm2; 5分!!!!!!!!! (2)如 解 图 ②、③,设 剪 开 的 三 角 形 的 短 边 长 为 xcm, 依题意得:(13-x)(13+13-x)=13×13-1, 8分 ! !!!!!!!!!!!!!!!!!! 解得 x1 =5,x2 =34(舍去), 故能将 13cm×13cm的正方形做这样的剪开拼合, 可以拼合成一个 8cm×21cm的长方形,但面积 少了 1cm2. 10分!!!!!!!!!!!!!!!! 第 23题解图② 第 23题解图③ 24.(1)证明:由旋转 45°,可知:∠ADE=∠ABC=90°, ∠EAD=∠CAB=45°,AE=AC,AD=AB, ∴在△CAE中,∠ACE=∠AEC=67.5°, 在△DAB中,∠ABD=∠ADB=67.5°, 1分!!! ∴∠FDC=∠ADB=67.5°,∴∠FDC=∠DCF, ∴CF=DF, 2分!!!!!!!!!!!!!! 在 Rt△EDC中,∠CED=∠EDF=22.5°, ∴EF=DF, ∴EF=CF; 3分!!!!!!!!!!!!!! (2)解:成立;方法一:如解图①,过点 E作 EG∥CB 交 BF延长线于点 G. 4分!!!!!!!!!! 第 24题解图① ∵AD=AB, ∴∠ADB=∠ABD. ∵∠EDG+∠ADB=∠CBF+∠ABD=90°, ∴∠EDG=∠CBF. ∵EG∥CB, ∴∠G=∠CBF. ∴∠EDG=∠G. ∴EG=ED. ∵ED=BC, ∴EG=BC. 6分!!!!!!!!!!!!!! ∵∠EFG=∠CFB, ∴△FEG≌△FCB(AAS). ∴EF=CF; 7分!!!!!!!!!!!!!! 方法二:如解图②,分别过点 A,C,E,作 AP⊥BF于 点 P,CN⊥BF于点 N,EM⊥BF交 BF延长线于点 M. 4分!!!!!!!!!!!!!!!!!! 第 24题解图② 证△EMD≌△DPA, 得 EM=PD, 证△APB≌△BNC, 得 CN=BP, 又等腰△ABD中,AP⊥BD, 得 PD=PB,故 EM=CN, 6分!!!!!!!!! 故△EMF≌△CNF(AAS), 因此 EF=CF; 7分!!!!!!!!!!!!! 方法三:过点 C作 CP∥DF交 ED延长线于点 P,EP 交 BC于点 Q. 4分!!!!!!!!!!!!! 由∠EDF=∠BDQ,∠EDF=∠DBC, 得∠BDQ=∠DBQ, 则 DQ=BQ, 又 CP∥BD, 得∠QCP=∠QBD,∠QPC=∠QDB, 则∠QCP=∠QPC,可得 CQ=PQ, 故 CQ+QB=PQ+DQ,PD=BC=DE, 6分!!! 因此EF CF=ED DP=1,即 EF=CF; 7分!!!!!!! (3)解:如解图③,过点 A作 AP⊥BD于点 P. 第 24题解图③ ∵AB=AD,∴∠PAB=1 2∠DAB=α 2. ∵∠PAB+∠PBA=∠CBD+∠PBA=90°,∴∠CBD =∠PAB=α 2, ∵AE AD=AC AB 槡= 2,∠EAC=∠DAB.∴△AEC∽△ADB , 32 ∴CE BD=AE AD 槡= 2. ∵∠ACE=∠ABD.∴∠CFB=∠CAB=45°, 9分 !!! !!!!!!!!!!!!!!!!!! ①当∠CDF=90°时,如解图④,△CDF为等腰直角 三角形,则 CF 槡= 2DF, 第 24题解图④ ∵EF=CF, ∴CF=槡2 2BD. ∴DF=1 2BD. ∵CD=DF, ∴CD=1 2BD. ∴tanα 2=tan∠CBD=CD BD=1 2; 11分!!!!! ②当∠FCD=90°时,如解图⑤,△CDF为等腰直角 三角形,则 CF=槡2 2DF,过点 C作 CG⊥DF于点 G. 第 24题解图⑤ ∵EF=CF, ∴CF=槡2 2BD. ∴DF=BD. ∵CG⊥DF, ∴CG=1 2DF. ∴CG=1 3BG. ∴tanα 2=tan∠CBG=CG BG=1 3. 12分!!!!!! 综上所述:tanα 2=1 2或 1 3. 25.(1)证明:联立 y=kx2 +ax+a, y=kx2 +bx+b{ , 1分!!!!!! 得 kx2 +ax+a=kx2 +bx+b. 整理,得(a-b)x=b-a. ∵a≠b,∴x=-1,∴ x=-1, y={ k. 2分!!!!!! ∴函数 y1与 y2的图象交点坐标为(-1,k). 所以该交点落在直线 x=-1上. 3分!!!!! (2)解:分别令 y1 =0,y2 =0,得 kx2 +ax+a=0,kx2 +bx+b=0. 则 a2 -4ak>0,xA,B =-a± a2 -4槡 ak 2k , b2 -4bk>0,xC,D =-b± b2 -4槡 bk 2k , 5分!!!! ∴AB= a2 -4槡 ak |k| ,CD= b2 -4槡 bk |k| . 6分!!!! ∵AB=CD,∴ a2 -4槡 ak |k| = b2 -4槡 bk |k| . ∴a2 -4ak=b2 -4bk.∴(a+b)(a-b)=4k(a-b). ∵a≠b,∴a+b=4k. 又∵a2 -4ak>0,∴a2 -a(a+b)>0,得 ab<0. 故 a+b=4k且 ab<0. 8分!!!!!!!!!! (3)解:若 k>0时, ①当点 C在点 B左侧,则 AC=BC=BD,∴AB=CD. ∴xC -xA =xB -xC.∴2xC =xA +xB. 9分!!!!! ∴ 2 · -b- b2 -4槡 bk 2k = -a- a2 -4槡 ak 2k + -a+ a2 -4槡 ak 2k .∴a-b= b2 -4槡 bk. ∴(a-b)2 =b2 -4bk且 a>b,整理得 a2 +b2 -ab= 0, 10分!!!!!!!!!!!!!!!!!! 依题意 b≠0,得(a b)2 -a b+1=0,Δ=1-4=-3 <0, ∴不存在实数 a,b,使得 B,C为线段 AD的三等分 点. 11分!!!!!!!!!!!!!!!!! ②当点 C在点 B右侧,则 AB=BC=CD. ∴xB -xA =xC -xB,∴2xB =xA +xC, 12分!!!! ∴ 2 · -a+ a2 -4槡 ak 2k = -a- a2 -4槡 ak 2k +-b- b2 -4槡 bk 2k , 由(2)得 a2 -4槡 ak= b2 -4槡 bk,则 4 a2 -4槡 ak=a -b, ∴16(a2 -4ak)=(a-b)2 且 a>b,则 -16ab=a2 - 2ab+b2, 整理,得:a2 +14ab+b2 =0, 13分!!!!!!! 依题意 b≠0,得:(a b)2 +14· a b+1=0.解得:a b= -14± 142 槡 -4 2 槡=-7±4 3. ∵由(2)得 a+b=4k>0且 ab<0,又 a>b, ∴a>0>b,且 a>-b, ∴ a b<-1 , 42 ∴ a b 槡=-7+4 3(舍去),则 a b 槡=-7-4 3. 若 k<0时,同理可得 a b 槡=-7-4 3. 14分!!! 综上所述,存在这样的函数 y1,y2,使得 B,C为线段 AD的三等分点,且 a b 槡=-7-4 3 . 52 2019年宁德市初中毕业班质量检测数学参考答案 一、选择题:(本大题有 10小题,每小题 4分,满分 40 分) 1.B 【解析】正数的绝对值是它本身,则 2019的绝对 值是 2019. 2.C 【解析】逐项分析如下: 选项 逐项分析 正误 A 圆柱的主视图、左视图都是长方形, 俯视图是圆,不符合题意 × B 圆锥的 主 视 图 是 三 角 形,俯 视 图 是 圆,不符合题意 × C 球的主视图、俯视图、左视图都是圆, 符合题意 √ D 六棱柱的主视图是矩形,俯视图是六 边形,不符合题意 × 3.D 【解析】逐项分析如下 选项 逐项分析 正误 A a3·a2 =a5≠a6 × B a6 ÷a2 =a4≠a3 × C (槡2)0 =1≠0 × D 3-2 =1 9 √ 4.B 【解析】∵5-3=2,5+3=8,根据三角形任意两 边之和大于第三边,任意两边之差小于第三边可得:2 <x<8,∴x的值可以是 5. 5.D 【解析】把每个小正方形的边长看作 1,则 AB= BN=2,由勾股定理可得 AM=BM= 12 +3槡 2 槡= 10, ∴△ABN是等腰直角三角形,△ABM是等腰三角形, 故所得三角形是等腰三角形是必然事件. 6.C 【解析】∵Δ=(-2)2 -4×1×(-1)=8>0,∴ 原方程有两个不相等的实数根. 7.B 【解析】设这批谷米内夹谷 x石,由题意得 28 254= x 1534,解 得 x≈169,∴ 这 批 谷 米 内 夹 有 谷 粒 约 是 169石. 8.A 【解析】由函数图象可知:开始销售了 40千克,销 售金额为 600元;余下的每千克降价 3元,直至全部 售完,总共销售金额为 720元,∴开始每千克的售价 为:600÷40=15(元/千克),销售余下的杨梅每千 克:15-3=12(元),销 售 量为:720-600 12 =10(千 克),小卖部从批发市场共购进杨梅:40+10=50(千 克),花费了:720-220=500(元);所以这批杨梅的 进价是 500÷50=10(元 /千克). 第 9题解图 9.A 【解析】如解图,连接 OD,AD, ∵AB是⊙O的直径,∴ ∠ADB= 90°,∴AD⊥BC,∵AB=AC,∴BD =CD,∠BAD=∠CAD,即 ) BD= ) DE;∵OA=OB,BD=CD,∴OD是 △ABC的中位线,∴OD∥AC,∵点 F是 CE的中点, ∴DF是 △BCE的 中 位 线,∴ DF∥ BE,∵ ∠AEB= 90°,∴∠ODF=∠AFD=∠AEB=90°,又∵OD是⊙O 的半径,∴DF是 ⊙O的切线;∵ AB=AC,∠AEB= 90°,AE与 BE的长度无法判断相等,∴∠A与∠ABE 不一定相等,故选 A. 10.B 【解析】∵A(2,m),B(2,m-5),∴AB2 =52 =25, 由勾股定理得,OA2 =22 +m2,OB2 =22 +(m-5)2, 当∠AOB=90°时,OA2 +OB2 =AB2,即 22 +m2 +22 + (m-5)2 =25,解得 m1 =4,m2 =1;当∠ABO=90° 时,OA2 =OB2 +AB2,即 22 +m2 =22 +(m-5)2 +25, 解得 m=5;当∠OAB=90°时,OB2 =OA2 +AB2,即 22 +(m-5)2 =22 +m2 +25,解得 m=0;综上所述,m 的值不可能是 2. 二、填空题:(本大题有 6小题,每小题 4分,满分 24分) 11.2.94×106 【解析】绝对值大于 10的数用科学记数 法表示为 a×10n 的形式时.其中 1≤ |a|<10,n为 整数,且 n=原数的整数位数 -1,∴2940000=2.94 ×106. 12.60 【解析】∵CD∥AB,∠1=30°,∴∠C=∠1= 30°.∵DA⊥ CE∴∠CAD=90°,∴ ∠D=90°-30° =60°. 13.1 3 【解析】用 A,B,C分别表示给九年级的三辆车, 画树状图如解图: 第 13题解图 由树状图可知,共有 9种等可能的情况,其中小明和 小慧搭乘同一辆车的情况有 3种,∴P(小明和小慧 搭乘同一辆车)=3 9=1 3. 14.x≤ -1 【解析】由数轴可得这两个不等式的解集 分别为:x≤ -1和 x<1,则该不等式组解集为:x≤ -1. 15.② 【解 析 】原 式 = x-3 (x+1)(x-1) - 3 1-x = 62 x-3 (x+1)(x-1)+ 3(x+1) (x+1)(x-1)= 4x (x+1)(x-1) ∴他开始出现计算错误的是在第②步. 第 16题解图 16.1 【解析】如解图,过点 G作 GH ⊥AD于点 H,在矩形 AEFG中,AG =EF,∠GAE=∠GAD+∠DAE= 90°,∵四边形 ABCD是正方形,∴ ∠BAE+∠DAE=90°,∴∠GAD= ∠BAE;同理:∠BAE=∠FEC,∴ ∠GAD=∠FEC,又∵∠GHA=∠C=90°,∴△GAH ≌△FEC,∴GH=FC,设 BE=x,GH=FC=y,则 EC =4-x,∵ ∠B =∠C =90°,∠BAE =∠FEC, ∴△ABE~△ECF,∴ AB EC=BE CF,即 4 4-x= x y,∴y= -1 4x2 +x=-1 4(x-2)2 +1,∴当 x=2时,y有最 大值 1;即 G到 AD距离的最大值是 1. 三、解答题(本大题共 9小题,共 86分.请在答题卡 獉獉獉 的相 应位置作答) 17.解:原式 =x2 -6x+9+2x+x2 -9 4分!!!!! =2x2 -4x; 5分!!!!!!!!!!!!!!! 当 x 槡=- 3时, 原式 =2× 槡( )- 32 -4× 槡( )- 3 6分!!!!!! 槡=6+4 3. 8分!!!!!!!!!!!!!!! 第 18题解图 18.证明:如解图,∵AF=CD, ∴AF+FC =CD+FC. ∴AC=FD. 2分!!!! ∵点 F,G分别是 AC,AB的 中点, ∴GF∥BC. 4分!!!!!!!!!!!!!! ∴∠BCA =∠EFD. 5分!!!!!!!!!!! ∵BC=EF, ∴△ABC≌△DEF(SAS). 8分!!!!!!!! 19.解:设 A型号航模单价为 x元,B型号航模单价为 y 元,根据题意,得 1分!!!!!!!!!!!! 8x+5y=2200, 4x+6y=1520{ . 5分!!!!!!!!!!!! 解得 x=200, y=120{ . 7分!!!!!!!!!!!!! 答:A型号航模的单价为 200元,B型号航模的单价 为 120元. 8分!!!!!!!!!!!!!!! 20.解:(1)④; 2分!!!!!!!!!!!!!!! (2)x - =75.2×30+71.2×25+72.8×25 80 =73.2(分). 5分!!!!!!!!!!!!!! 答:这 80名同学的平均成绩为 73.2分; (3)小颖同学在自己班级托底同学中排名更靠前. 6分!!!!!!!!!!!!!!!!!! 理由:∵70>68,∴小颖同学成绩处于自己班级托底 同学的中上水平; ∵74<75,∴小榕同学成绩处于自己班级托底同学 的中下水平,且这两个班的参加托底训练的人数相 同,所以小颖在自己班级的排名更靠前. 8分!! 21.(1)证明:∵四边形 ABCD是菱形, ∴AC⊥BD,AB∥CD. ∴∠FBE=∠ODC. 2分!!!!!!!!!!! 又∵EF垂直平分 AB, ∴∠BFE=∠DOC=90°. ∴△BEF∽△DCO; 4分!!!!!!!!!!! (2)解:∵四边形 ABCD是菱形, ∴OC=1 2AC=1 2×12=6,CD=AB=10. 在 Rt△DCO中,根据勾股定理得, OD= CD2 -OC槡 2 = 102 -6槡 2 =8. 又∵EF垂直平分 AB, ∴BF=1 2AB=1 2×10=5. 6分!!!!!!!! 由(1)可知△BEF∽△DCO, ∴EF OC=BF DO,即EF 6 =5 8. ∴EF=15 4. 8分!!!!!!!!!!!!!!! 22.解:(1)根据图象上 A,B两点的位置可知:xB >2. ∴ -2x+2>2. 3分!!!!!!!!!!!!! ∴x<0; 4分!!!!!!!!!!!!!!!! (2)解法一:∵x<0, ∴xC =-x>0. ∴点 C在第一象限内. 5分!!!!!!!!!! 由 xB -xC,得 -2x+2-(-x) =-x+2. ∵ -x>0, ∴ -x+2>2>0. ∴xB >xC. ∴0<xC <xB. 7分!!!!!!!!!!!!!! ∵反比例函数在第一象限内,y随 x的增大而减小, ∴y2 >y1. 8分!!!!!!!!!!!!!!! 解法二:∵x<0, ∴ -x>0. ∴xC >0. ∴点 C在第一象限内. 5分!!!!!!!!!! ①若 xC =xB,即 -x=-2x+2, 得 x=2,这与 x<0矛盾, ∴点 C不与点 B重合; ②若 xC >xB,即 -x>-2x+2, 得 x>2,这与 x<0矛盾, ∴点 C不在点 B右侧; ③若 xC <xB,即 -x<-2x+2 , 72 得 x<2, ∵x<0满足 x<2, ∴点 C在点 B左侧.(也可由①②直接判断点 C在 点 B左侧) 7分!!!!!!!!!!!!!!! ∵反比例函数在第一象限内,y随 x的增大而减小, ∴y2 >y1. 8分!!!!!!!!!!!!!!! 23.解:(1)矩形. 2分!!!!!!!!!!!!!! (2)作图如解图①; 5分!!!!!!!!!!! 第 23题解图① ∴所作的点 O是四边形 ABCD的外心,四边形 ABCD 就是所求作的四边形. 6分!!!!!!!!!! (3)解法一:如解图②,∵点 O是四边形 ABCD的 外心, ∴OA=OC=OB=OD, ∴点 A,B,C,D都在以 OC为半径的⊙O上. 8分 !! !!!!!!!!!!!!!!!!!! 连接 OB,OC,作 OM⊥BC于点 M. 则∠OMB=90°,∠BOC=2∠BDC. ∵OC=OB, ∴∠COM=1 2∠BOC=∠BDC,CM=1 2BC=4. 11分 ! !!!!!!!!!!!!!!!!! ∴OC= CM sin∠COM=4÷4 5=5. 12分!!!!!! 第 23题解图② 第 23题解图③ 解法二:如解图③,∵点 O是四边形 ABCD的外心, ∴OA=OC=OB=OD, ∴点 A,B,C,D都在以 OC为半径的⊙O上. 8分 !! !!!!!!!!!!!!!!!!!! 延长 CO交⊙O于点 E,连接 EB, 则∠EBC=90°,∠BEC=∠BDC. ∴CE= BC sin∠BEC=8÷4 5=10. 11分!!!!!! ∴OC=1 2CE=5. 12分!!!!!!!!!!! 24.(1)证明:∵四边形 ABCD是矩形, ∴AD∥BC. ∴∠FEB=∠EBC. 2分!!!!!!!!!!! 根据对称可得∠FBE=∠EBC, ∴∠FEB=∠FBE. ∴BF=EF. 4分!!!!!!!!!!!!!! 第 24题解图① 第 24题解图② (2)证明:解法一:(如解图②) 分别过点 A作 AG⊥BC′于点 G,AH⊥C′D′于点 H, ∵四边形 ABCD是矩形, ∴∠BAD =90°. ∴tan∠ABE=AE AB= 4 3槡3 4 =槡3 3. ∴∠ABE =30°. 5分!!!!!!!!!!!! ∴∠FEB=90°-∠ABE=60°. ∴∠FBE=∠FEB=60°. 6分!!!!!!!!! ∴∠ABG=∠FBE-∠ABE=30°. ∴AG=1 2AB=2. 7分!!!!!!!!!!!! 根据对称可得∠BC′D′=∠C=90°,C′D′=CD. ∴∠BC′D′=∠C′GA=∠C′HA=90°. ∴四边形 AGC′H是矩形. ∴AG=C′H=2. ∴AH是 C′D′的垂直平分线. 8分!!!!!!! ∴AC′=AD′. ∴△AC′D′是等腰三角形. 9分!!!!!!!! 解法二:(如解图③) 延长 D′A交 BF于点 G. 同解法一得∠FBE=∠FEB=60°. 6分!!!!! 证得 AF=EA, 7分!!!!!!!!!!!!! 再证△D′AE≌△GAF. 8分!!!!!!!!!! 得 AD′=AG,从而得 AC′=AD′=1 2GD′. 9分! 第 24题解图③ 第 24题解图④ 解法三:(如解图④) 过点 A作 MN∥C′D′分别交 BF,D′E于点 M,N, 同解法一得∠FBE=∠FEB=60°. 6分!!!!! 证得 AF=EA, 7分!!!!!!!!!!!!! 证△AFM≌△AEN得到 AM=AN. 8分!!!!! 再证△AMC′≌△AND′.得到 AC′=AD′. 9分!! 解法四:(如解图② -④ ) 82 由勾股定理得 BE=8 3槡3. 设 BF=x,由(1)得 AF=x-4 3槡3. 由勾股定理解得 BF=8 3槡3,AF=4 3槡3. ∴AF=EA,∠ABF=30°. 7分!!!!!!!!! 以下同各解法. (3)解:解法一:(如解图⑤)根据对称可得点 C′与点 D′的对称点分别为点 C,D. 作点 A关于 BE的对称点点 A′,连接 A′C、A′D、A′B. 由对称性得 △A′CD≌△AC′D′,BA′=BA. ∴S△A′CD =S△AC′D′,点 A′落在以点 B为圆心以 AB为 半径的 ) AM上. 11分!!!!!!!!!!!!! 设 ) AM交 BC于点 M,过点 A′作 A′N⊥CD于 N,连接 A′B. 由垂线段最短知 BA′+A′N≥BM+MC. ∵BA′=BM,∴ A′N≥MC. ∴当点 A′落在点 M处时△A′CD的面积最小. 即△AC′D′的面积最小. 此时 MC=BC-BM=2. S△AC′D′=S△A′CD =1 2MC·DC=4. ∴△AC′D′面积的最小值为 4. 13分!!!!!! 第 24题解图⑤ 第 24题解图⑥ 解法二:(如解图⑥) 作矩形 BC′D′J,过点 A作 AH⊥C′D′于点 H,延长 HA 交 BJ于点 I. ∴AH+AI=HI=BC′=6. ∴AH=6-AI. ∴AH随的 AI增大而减小. 11分!!!!!!!! ∵AI≤AB, ∴AI=AB时,AI取得最大值 4. 此时,AH取得最小值 2. ∴S△AC′D′=1 2C′D′·AH=4. ∴△AC′D′面积的最小值为 4. 13分!!!!!! 25.解:(1)如解图①,∵v0 2 =vx 2 +vy 2,θ=53°, ∴vx=v0cosθ=15×3 5=9, 2分!!!!!!!! vy=v0sinθ=15×4 5=12. 3分!!!!!!!! 第 25题解图① 第 25题解图② (2)由(1)得 vx=9,vy=12. 根据题意,得 d=vyt-5t2 =12t-5t2,yM -yA =d. ∴点 M的横坐标为:x=vxt=9t,① 纵坐标为:y=d+15=-5t2 +12t+15.② 6分!! 由①得 t=x 9,代入②得 y=-5 81x2 +4 3x+15. 8分 ! !!!!!!!!!!!!!!!!!! (3)∵坡顶的铅直高度为 15米,山坡的坡比为 1 3, ∴OB=15÷1 3=45(米). ∴A点的坐标为(0,15),B点的坐标为(45,0). 设线段 AB的函数关系式为:y=kx+b.将 A,B两点 坐标代入上式,得 15=b, 0=45k+{ b. 解得 b=15, k=-1 3{ . ∴线段 AB的关系式为:y=-1 3x+15. 10分!! 由 y=-5 81x2 +4 3x+15, y=-1 3x+15{ . 解得 x=27, y=6{ . ∴水流在山坡上的落点 C离喷射点 A的水平距离 是 27米. 11分!!!!!!!!!!!!!!! 如解图②,过点 C作 CD⊥x轴,垂足为 D,得 CD=6, BD=18. 在 Rt△DCB中,根据勾股定理,得 BC= CD2 +BD槡 2 = 62 +18槡 2 槡=6 10(米). 由平移的性质可得,需要把喷射点沿坡面 AB方向 移动 槡6 10米. 13分 !!!!!!!!!!!!! 92 2019年龙岩市九年级学业(升学)质量检查试题解析 一、选择题:本大题共 10小题,每小题 4分,共 40分. 1.B 【解析】∵实数 a,b所表示的数恰好在整数点 上,由图可知 a=-3,b=2.∴a+b=-3+2=-1, 故选 B. 2.A 【解析】A既是轴对称图形.又是中心对称图形, 故 A正确;B是轴对称图形,但不是中心对称图形, 故 B不正确;C是轴对称图形,但不是中心对称图 形,故 C不正确.D是轴对称图形,但不是中心对称 图形,故 D不正确. 3.C 【解析】A.汀江流域范围较大,适合用抽样调查, 故 A选项错误;B.市场上粽子数量较大,宜用抽样调 查,故 B选项错误;C.40名同学,数量不多,范围较 小,宜采用全面调查,故 C选项正确;D.烟花爆竹具 有破坏性,不宜用全面调查,故 D选项错误. 4. A 【解 析 】 把 x=a, y={ b 代 入 2x+y=3, 3x-2y{ =7得 2a+b=3, 3a-2b=7{ ,两式相加得 5a-b=10.故选 A. 5.C 【解析】A.∠1与∠2为对顶角,两角相等,故 A 错误;B.取直线平行内错角相等,当平行时有∠1= ∠2,故 B错误;C.三角形的外角大于不相邻的任一 内角,∠1>∠2,故 C正确;D.在同圆或等圆中,相等 的弧所对圆周角相等,则∠1=∠2,故 D错误. 6.A 【解析】解不等式 2x-1>3(x-2)得 x<5,作示 意图如解图,由于不等式组的解集为 x<5,故 m≥5. 第 6题解图 第 7题解图 7.D 【解析】如解图,面积 x=AB2,y=AC2,z=BC2,在 Rt△ABC中,AB2 =AC2 +BC2,故 x=y+z,应选 D. 第 8题解图 8.B 【解析】如解图,∵图中是三 个 等 边 三 角 形,∠3=60°,∴ ∠BAC=180°-∠3-60°=60°, ∠ABC=180°-∠1-60°=120° -∠1,∠ACB=180°-∠2-60° =120°-∠2,∵ ∠BAC+∠ABC +∠ACB=180°,∴60°+(120°- ∠1)+(120°-∠2)=180°,∴∠1+∠2=120°,故 选 B. 9.C 【解析】∵抛物线开口向下,∴a<0,∵顶点为 (1,n).∴对称轴 x=-b 2a=1,b=-2a,∴3a+b= 3a-2a=a<0,故 A正确;∵点 A(-1,0),∴代入抛 物线中得 a-b+c=0,∴a+2a+c=0,解得 c=- 3a,又∵3≤c≤6,∴3≤ -3a≤6,则 -2≤a≤ -1.故 B正确;∵a<0,b=-2a>0,c>0,∴abc<0,故 C错 误;∵抛物线对称轴为 x=1且过点 A(-1,0),故抛 物线与 x轴的另一交点为(3,0),代入 y=ax2 +bx+ c得 9a+3b+c=0,又∵c>0,∴9a+3b+c+c>0, 即 9a+3b+2c>0,故 D正确. 10.D 【解析】∵144=122 =24 ×32,∴144的所有正约 数之和为(1+2+22 +23 +24)(1+3+32)=403.规 律:若整数 M=am·bn.则 M的所有正约数之和为: (1+a+a2 +a3 +… +am)(1+b+b2 +b3 +…bn). 二、填空题:本大题共 6小题,每小题 4分,共 24分. 11.-1 2 【解析】原式 = 1 (-2)1 =-1 2. 12.1 3 【解析】∵袋中共有 6个球,其中白球有 2个. ∴从中任意摸出一个球是白球的概率为 2 6=1 3. 第 13题解图 13. 槡2 2 3 【解析】如解图,∠C= 90°,sinA=BC AB=1 3,设 BC=k, 则 AB=3k,∴AC= AB2 -BC槡 2 槡=2 2k,∴cosA= AC AB= 槡2 2k 3k = 槡2 2 3 . 14.3 【解析】根据题意得:a2 -2a+3=b2 -2b+3,∴ (a-b)(a+b-2)=0,∵a≠b,∴a+b-2=0,则 a +b=2,∴当 x=a+b=2时,x2 -2x+3=22 -2×2 +3=3. 15. 槡3 3 2 -2π 3 【解析】如解图,连接 OE,OF,EF.∵CD 第 15题解图 为⊙O的切线,∴ OE⊥ CD,∵ ∠C=30°,OE= OB=2,∴∠COE=60°, OC=2OE=4,CE=OC ·sin60° 槡=2 3,∵ ) EF= ) EB,∴ ∠1=∠2= 1 2 ∠EOC=30°,∴∠AOF=∠EOF=∠EOC=60°.∴ ∠ADC=90°,又∵AE=CE 槡=2 3.∠1=30°,∴DE 槡= 3,AD=DE·tan60°=3,S△ADE =1 2·AD·DE= 1 2 槡×3× 3= 槡3 3 2 .又 S△AEF =S△OEF(同底等高),∴ S阴 =S△ADE -S扇OEF = 槡3 3 2 -60 360·π·22 = 槡3 3 2 -2π 3. 16.槡41 【解析】如解图,将△ABP绕点 B 逆时针旋转 03 第 16题解图 60°得到△A′BP′,连接 AA′, PP′,由旋转性质可知,△A′ BA和 △PP′B均 为 等 边 三 角形.PP′=PB.A′B=AB= 4.∴PA+PB+PC=P′A′+ PP′+PC,∴ 当 P′A′+PP′ +PC=A′C时,PA+PB+PC值最小,此时 A′、P′、 P、C四点共线,即当 A′、P′、P、C四点共线时,PA+ PB+PC的最小值为 A′C,∵∠ABC=30°,∠A′BA= 60°,∴在 Rt△A′BC中,A′B=AB=4.BC=5,A′C= A′B2 +BC槡 2 = 42 +5槡 2 槡= 41.∴PA+PB+PC的 最小值为 槡41. 三、解答题:本大题共 9小题,共 86分. 17.解:方程两边同乘以 x(x-1)得 x2 -2(x-1)=x(x -1), 4分!!!!!!!!!!!!!!!! 整理得:-x=-2,解得 x=2. 6分!!!!!! 检验:当 x=2时,x(x-1)=2≠0. 7分!!!!! ∴x=2是原方程的解. 8分!!!!!!!!! 18.解:原式 = x-2 (x+1)2 ÷(x2 +x x+1- 3x x+1) 3分!!!! = x-2 (x+1)2· x+1 x(x-2) 5分!!!!!! = 1 x(x+1). 6分!!!!!!!!!! 当 x=1 3时,原式 = 1 1 3×4 3 =9 4. 8分!! 第 19题解图① 19.解:(1)证明:如解图①,过点 C 作 CE∥AD交 AB于点 E. 1分 ! !!!!!!!!! ∵CE∥AD, ∴∠A=∠1, ∵∠A=∠B, ∵∠1=∠B, ∴CE=BC. 2分!!!!!!!!!!!!!! ∵AB∥CD,CE∥AD, ∴四边形 AECD为平行四边形, 3分!!!!!! ∴AD=CE, ∴AD=BC; 4分!!!!!!!!!!!!!! (2)如解图②,分别过点 D,C作 DE⊥AB,CF⊥AB, 垂足为 E,F, 5分!!!!!!!!!!!!!! 第 19题解图② ∴DE∥CF, ∵AB∥CD, ∴四边形 DEFC为矩形, ∴DE=CF. 6分!!! 在 Rt△DAE 中,∠A= 60°,AD=2, ∴sin60°=DE AD,即槡3 2=DE 2, ∴DE 槡= 3. 7分!!!!!!!!!!!!!! 在 Rt△CBF中,∠B=45°,CF=DE 槡= 3, ∴BC 槡= 2CF 槡= 6. 8分!!!!!!!!!!! 20.解:如解图,点 M,N即为所求作的点. 2分!!! 第 20题解图 已知:如解图,△ABC中,点 M,N分别是 AB,AC的中点, 连接 MN. 求证:MN∥BC.MN=1 2BC. 4分!!!!!!!! 证明:如解图,延长 MN至点 D,使得 MN=ND,连接 CD, 在△AMN和△CDN中, AN=CN, ∠ANM=∠CND, MN=DN{ , ∴△AMN≌△CDN(SAS). 5分!!!!!!!! ∴∠AMN=∠D, ∴AM∥CD,即 BM∥CD. ∵AM=BM=CD, ∴四边形 BMDC为平行四边形. 6分!!!!! ∴MN∥BC,MD=BC. 7分!!!!!!!!!! ∵MN=1 2MD, ∴MN=1 2BC. 8分!!!!!!!!!!!!! 21.(1)解:原式 =1-1 2 +1 2-1 3 +1 3-1 4+1 4 -1 5 +1 5-1 6=1-1 6=5 6; 4分!!!!!!!!! (2)证明: 解法一: 1 1×3+ 1 2×4+ 1 3×5+ 1 4×6 =1 2(1-1 3)+1 2(1 2 -1 4)+1 2(1 3 -1 5)+1 2 (1 4-1 6) =1 2(1-1 3+1 2-1 4+1 3-1 5+1 4-1 6)=17 30. 7分!!!!!!!!!!!!!!!!!! ∵ 1 3=10 30,4 5=24 30, ∴ 1 3=10 30<17 30<24 30=4 5,即原式得证. 8分!!! 解法二: ∵ 1 2×3+ 1 3×4+ 1 4×5+ 1 5×6< 1 1×3+ 1 2×4+ 1 3×5 + 1 4×6< 1 1×2+ 1 2×3+ 1 3×4+ 1 4×5, 6分!!!! ∴ 1 2-1 3 +1 3 -1 4 +1 4 -1 5 +1 5 -1 6 < 1 1×3 + 13 1 2×4+ 1 3×5+ 1 4×6<1-1 2 +1 2 -1 3 +1 3 -1 4 + 1 4-1 5. ∴ 1 3 < 1 1×3+ 1 2×4+ 1 3×5+ 1 4×6<4 5,即原式得 证. 8分!!!!!!!!!!!!!!!!!! 22.解:(1)W1 =(160-2x)(50+x)=-2x2 +60x+ 8000, 2分!!!!!!!!!!!!!!!!! W2 =20(50-x)=-20x+1000; 4分!!!!! (2)依题意得:W=W1 +W2 =-2x2 +40x+9000= -2(x-10)2 +9200. 8分!!!!!!!!!! ∵x为正整数,∴当 x=10时,总利润 W最大,最大 值为 9200元. 10分!!!!!!!!!!!!! 23.解:(1)5000,补全的条形统计图如解图; 第 23题解图 (2)4%,18; (3)观点 B占的百分比 =1-46% -30% -15% - 4% =5%, 9分!!!!!!!!!!!!!!! 300×(46% +5% +15%)=300×66% =198万. 答:该市持 A、B、D观点赞成数字化阅读的人数约 有 198万人. 10分!!!!!!!!!!!!! 24.(1)证明:如解图,连接 AD. 1分!!!!!!! 则由同弧所对的圆周角相等可知∠ACF=∠ADF. 2分!!!!!!!!!!!!!!!!!! 第 24题解图 又 AE是 由 线 段 AC 绕点 A逆 时 针 旋 转 90°得到,∴AC=AE. 3分!!!!! ∵AB为⊙O直径, CD⊥AB, ∴AC=AD=AE, ∴∠AED=∠ADF. 4分!!!!! ∴∠ACF=∠AED; 5分!!!!!!!!!!! (2)解:是定值槡2,理由如下: 6分!!!!!!! 如解图,过点 E作 EN∥CD,过点 D作 DN⊥CD,且 EN与直线 AB的反向延长线交于点 M,与直线 DN 交于点 N, 7分!!!!!!!!!!!!!!! ∵∠EAC=∠CPA=90°, ∴∠EAM+∠CAB=∠CAB+∠ACP=90°. ∴∠EAM=∠ACP,同理∠MEA=∠CAB. 又 AC=AE, ∴△EAM≌△ACP(ASA), 8分!!!!!!!! ∴EM=AP,AM=CP. 9分!!!!!!!!!! ∵DN⊥CD,CD⊥AB, ∴DN∥AB,又 EN∥CD, ∴四边形 MNDP是矩形, ∴MN=PD,MP=ND. ∵AB是⊙O的直径,CD⊥AB, ∴MN=PD=CP=AM. 又∵EM=AP,∴EM+MN=AP+AM,即 EN=MP =ND, ∴△END是等腰直角三角形, ∴∠EDN=45°. 11分!!!!!!!!!!!! ∵DN∥AB, ∴∠EGM=∠EDN=45°, ∴EG AP=EG EM= 1 sin∠EGM 槡= 2. 12分!!!!!! 25.解:(1)∵直线 y=x+t与双曲线 y=k x相交, 由 k x=x+t得 x2 +tx-k=0, ∴x=-t± t2 +4槡 k 2 . 2分!!!!!!!!!! 设 C(xC,yC),D(xD,yD), 若 xC <xD,则 C(-t- t2 +4槡 k 2 ,t- t2 +4槡 k 2 ), D(-t+ t2 +4槡 k 2 ,t+ t2 +4槡 k 2 ). 若 xC >xD,则 D(-t- t2 +4槡 k 2 ,t- t2 +4槡 k 2 ), C(-t+ t2 +4槡 k 2 ,t+ t2 +4槡 k 2 ); 4分!!!!! (2)AB∥CD; 理由如下: 5分!!!!!!!!!!!!!!! 不妨设 xC <xD, 由(1)知 C(-t- t2 +4槡 k 2 ,t- t2 +4槡 k 2 ), D(-t+ t2 +4槡 k 2 , t+t2 +4槡 k 2 ) ∴A(-t- t2 +4槡 k 2 ,0),B(0,t+ t2 +4槡 k 2 ). 6分 !! !!!!!!!!!!!!!!!!!! 设直线 AB的解析式为 y=px+q, 则将 A,B两点坐标代入有: p· -t- t2 +4槡 k 2 +q=0, q=t+ t2 +4槡 k 2 ,所以 p=1, ∴直线 AB的解析式为 y=x+t+ t2 +4槡 k 2 , 7分 !! !!!!!!!!!!!!!!!!!! 23 ∴直线 AB与 CD的位置关系是 AB∥CD; 8分! (3)将 D(3,2)代入双曲线 y=k x(k>0)得 k=6, 将 D(3,2)代入直线 y=x+t,得 t=-1. ∴双曲线解析式为 y=6 x,直线解析式为 y=x-1. 由 6 x=x-1得 x1 =3,x2 =-2,∴C(-2,-3). 9分 ! !!!!!!!!!!!!!!!!!! ∵C(-2,-3),D(3,2)在抛物线 y=ax2 +bx+5(a ≠0)上, ∴ 4a-2b+5=-3, 9a+3b+5=2{ , 解得 a=-1, b=2{ , 即 y=-x2 +2x+5=-(x-1)2 +6. 10分!!! 由 mn<0,m<x<n,可知 m<0,n>0. ①当 0<n≤1,由函数的最小值为 2m,最大值为 2n 可知 -n2 +2n+5=2n, -m2 +2m+5=2m{ , ∴m,n即为一元二次方程 -x2 +2x+5=2x的两解 x 槡=± 5, 又 m<n,∴m 槡=- 5,n 槡= 5. 又∵0<n≤1,所以 m 槡=- 5,n 槡= 5不合题意; 11分 ! !!!!!!!!!!!!!!!!! ②当 1 2(m+n)≤1,即 m≤2-n时, 由 函 数 的 最 小 值 为 2m,最 大 值 为 2n 可 知 2n=6, -m2 +2m+5=2m{ , ∴ n=3, m 槡=- 5{ , 此时 m 槡=- 5≤ -1=2-3=2-n满足题意. ∴m+n 槡=- 5+3; 12分!!!!!!!!!! ③当 1 2(m+n)>1,即 m>2-n时,由函数的最小 值为 2m,最大值为 2n可知 2n=6, -n2 +2n+5=2m{ , ∴ n=3, m=1{ ,又∵m<0, ∴m=1,n=3不符合题意. 13分!!!!!!! 综上所述,满足题意的 m+n的值为 槡- 5+3. 14分 !! !!!!!!!!!!!!!!!!! 33 2019年三明市初中毕业班教学质量检测 数学试题参考答案及评分标准 说明:以下各题除本参考答案提供的解法外,其他解法参照本评分标准,按相应给分点评分. 一、选择题(每题 4分,共 40分) 1.C 【解析】逐项分析如下: 选项 逐项分析 正误 A -1+2=1≠ -1 B (-1)0 =1≠ -1 C -12 =-1 √ D (-1)-2 =1≠ -1 2.B 【解析】∵1亿 =108,∴682亿 =6.82×102 ×108 =6.82×1010. 3.A 【解析】左视图是从左向右看得到的物体的视图, 该几何体的左视图如选项 A所示. 4.B 【解析】∵不透明的袋子中只装有 4个黄球,没有 红球,∴摸到红球是不可能事件. 5.C 【解 析】∵ DE是 △ABC的中 位线,∴ △ADE∽ △ABC,相似比为 1∶2,则面积比为 1∶4,∵△ADE的 面积为 3,∴ S△ABC =4S△ADE =4×3=12,∴ 四 边 形 DECB的面积 =S△ABC -S△ADE =12-3=9. 第 6题解图 6.D 【解析】如解图,连接 BC,∵ 每个正方形的边长为 1,∴AB= 22 +1槡 2 槡= 5,BC= 22 +1槡 2 = 槡5,AC= 32 +1槡 2 槡= 10,∵AB2 +BC2 =AC2,∴ △ABC为 等 腰 直 角 三 角 形,∴ tan ∠BAC=BC AB=1. 7.A 【解析】∵2n +2n =1,∴2×2n =1,∴2n =1 2,则 n =-1. 第 8题解图 8.D 【解析】如解图,连接 OB,∵ AO⊥BC,BC=8,∴BD=4,∴在 Rt△BOD中,OD= OB2 -BD槡 2 = 3,∴ AD=AO+OD=8,∴ 在 Rt △ABD 中,AB = AD2 +BD槡 2 = 82 +4槡 2 槡=4 5. 9.D 【解析】∵抛物线的对称轴为直线 x=- -6 2×1=3, ∴x=-2和 x=8时,函数值相等,∵当 -2<x<-1 时,它的图象位于 x轴的下方;当8<x<9时,它的函数 图象位于 x轴的上方,∴抛物线与 x轴的交点坐标为 (-2,0),(8,0),把(-2,0)代入 y=x2 -6x+m中,解 得 m=-16. 10.A 【解析】如解图,连接 BE,CE,过点 E作 EG⊥BC 于点 G,∵ 四 边 形 ABCD是 正 方 形,∴ AB=AD, 第 10题解图 ∠BAC=∠DAC=45°,由旋转 的性 质 可 得,AB=AE,AC= AF,∠BAC=∠EAF=45°,∴ AE=AD,∠CAE+∠DAE= ∠DAE+∠FAD,∴ ∠CAE= ∠FAD,∴ △ADF≌ △AEC (SAS),∴DF=CE,∵∠BAE=60°,∴△ABE是等边 三角形,∴∠EBG=30°,∴EG=1 2BE=1 2,BG=槡3 2, ∴CG=1-槡3 2,∴在 Rt△CEG中,CE= EG2 +CG槡 2 = (1 2) 2 +(1-槡3 2)槡 2 = 槡8-4 3 槡 4 =槡 槡6- 2 2 . 二、填空题(每题 4分,共 24分) 11.125° 【解析】∵a∥b,∴∠2=180°-∠1=180°- 55°=125°. 12.丙 【解析】根据题意,乙、丙的平均数相同且高于 甲、丁的平均数,应在乙、丙中选择,而丙的方差小于 乙的方差,丙的成绩更稳定,所以应选的小组是丙. 13.-2<x≤1 【解析】解不等式 2x+4>0得 x>-2, 解不等式 x-3(x-2)≥ 4得 x≤1,∴该不等式组的 解集为 -2<x≤1. 14. x+y=100, 3x+1 3y=100{ . 第 15题解图 15. 槡3 3 2 -2π 3 【解析】如解图,连接 AE,根据题意得,AD=BC=AE=2, ∴BE=1 2BC=1,∴∠BAE=30°, ∴ ∠DAE=60°,CD=AB 槡= 3,∴ S阴影 =S梯形CEAD -S扇形EAD = 1 2 ×(1+2) 槡× 3- 60·π·22 360 = 槡3 3 2 -2π 3. 16. 槡4 3 【解析】如解图,过点 D作 DF∥OA交 OC于点 F,过点 C作 CE⊥OA于点 E,∵∠AOC=60°,∴tan ∠AOC 槡= 3,∴设 OE=x,CE 槡= 3x,∴x·槡3x 槡=4 3, 解得 x=2(负值舍去),∴OE=2,CE 槡=2 3,由勾股 定理得 OC=4,∴S菱形OABC =OA·CE 槡=4×2 3=8 槡3,∵四边形 OABC为菱形,∴AB∥CO,AO∥BC,∵ DF∥ AO,∴ S△ADO =S△DFO,同 理,S△BCD =S△CDF,∵ S菱形ABCO =S△ADO +S△DFO +S△BCD +S△CDF,∴S菱形ABCO =2 (S△DFO +S△CDF)=2S△CDO 槡=8 3,∴S△CDO 槡=4 3 . 43 第 16题解图 三、解答题(共 86分) 17.解:原式 =x2 -x-3x+4 x-1 · x-1 x2 -4 3分!!!!!! =(x-2)2 x-1 · x-1 (x+2)(x-2) 5分!!!! =x-2 x+2. 6分!!!!!!!!!!!! 当 x=1 2时,原式 = 1 2-2 1 2+2 7分!!!!!!!!! =-3 5. 8分!!!!!!!!! 18.证明:∵DE∥AC,CE∥BD, ∴四边形 OCED是平行四边形. 3分!!!!!! ∵四边形 ABCD是菱形, ∴AC⊥BD, ∴∠COD=90°. 6分!!!!!!!!!!!!! ∴四边形 OCED是矩形. 8分!!!!!!!!! 19.解:设直线 l的表达式为 y=kx+b(k≠0), 1分! 依题意,将 A、B两点代入得 -k+b=-4, k+b=0{ , 3分!!!!!!!!!!!!! 解得 k=2, b=-2{ , 7分!!!!!!!!!!!!! ∴直线 l的表达式为 y=2x-2. 8分!!!!!! 20.(Ⅰ)解:作图如解图; 4分!!!!!!!!!! 第 20题解图 (Ⅱ)证明:如解图,过点 P作 PD⊥BC于点 D, 由(Ⅰ)知 PA=PD. 又∵∠A=90°,PD⊥BC,BP=BP, ∴Rt△ABP≌Rt△DBP, ∴AB=DB. 6分!!!!!!!!!!!!!! ∵∠A=90°,AB=AC, ∴∠C=45°, ∴∠1=90°-45°=45°, ∴∠1=∠C, ∴DP=DC, ∴DC=AP, 7分!!!!!!!!!!!!!! ∴BC=BD+DC=AB+AP. 8分!!!!!!! 21.解:(Ⅰ)18°; 2分!!!!!!!!!!!!!! (Ⅱ)3; 4分!!!!!!!!!!!!!!!! (Ⅲ)每艘船乘坐人数的平均数约为 1×5% +2× 20% +3×45% +4×30% =3. 6分!!!!!! ∴每天需多安排 4人座的自划船的艘次为 300÷3= 100. 8分!!!!!!!!!!!!!!!!! 22.解:(Ⅰ)设惠好商场第一次购进这种玩具 x套, 依题意得 24000 x =50000 2x -10. 2分!!!!!!!!!!! 解得 x=100. 3分!!!!!!!!!!!!!! 经检验,x=100是该方程的根. 4分!!!!!! 答:惠好商场第一次购进这种玩具 100套; 5分! (Ⅱ)设剩余玩具每套的售价为 y元,则: 第二次进价为 50000÷200=250(元 /套), 6分!! (300-250)×4 5×200+(1-4 5)×200×(y-250) ≥50000×12% 8分!!!!!!!!!!!!! 解得 y≥200. 9分!!!!!!!!!!!!!! 答:剩余玩具每套售价至少要 200元. 10分!!! 23.(Ⅰ)证明:如解图,连接 OE,∵AB为直径, ∴∠ADB=90°,∴∠DAB+∠B=90°. 1分!!! ∵∠ADE和∠AOE都对着 ) AE, ∴∠AOE=2∠ADE. 2分!!!!!!!!!!! 又∵∠B=2∠ADE, ∴∠AOE=∠B. 3分!!!!!!!!!!!! 又∵∠C=∠DAB, ∴∠C+∠AOE=∠DAB+∠B=90°, ∴∠CEO=90°,∴OE⊥CE, 4分!!!!!!!! ∴CE是⊙O的切线; 5分!!!!!!!!!! 第 23题解图 (Ⅱ)解:如解图,连接 AE, ∵ ) AD= ) AD,∴∠1=∠B. 由(Ⅰ)知∠AOE=∠B, ∴∠1=∠AOE. 6分!!! 又∵∠2=∠2, ∴△EAF∽△OAE. 7分!!!!!!!!!!! ∴AE AF=AO AE=OE EF,即AE 3 =5 AE=5 EF. 8分!!!!! ∴EF=AE,AE2 =3×5=15. 9分!!!!!!!! ∴EF=EA 槡= 15. 10分!!!!!!!!!!! 24.(Ⅰ)证明:解法一:如解图①,∵ PD⊥AB,PE⊥AC, M为 AP中点, ∴DM=EM=1 2AP=AM. 2分!!!!!!!!! ∴∠1=∠2,∠3=∠4. 3分!!!!!!!!! ∴∠5=∠1+∠2=2∠1,∠6=∠3+∠4=2∠3. 5分 !!!!!!!!!!!!!!!!!! 53 ∴∠DME=∠5+∠6=2∠1+2∠3=2∠BAC; 6分 ! !!!!!!!!!!!!!!!!!! 第 24题解图① 解法二:∵ PD⊥AB,PE⊥AC,M为 AP中点, ∴DM=EM=1 2AP=AM=PM, 2分!!!!!! ∴点 A,D,P,E在以 M为圆心,MA为半径的圆上. 5分!!!!!!!!!!!!!!!!!! ∴∠DME=2∠BAC; 6分!!!!!!!!!!! (Ⅱ)解:如解图②,过点 M作 MN⊥DE于点 N, 第 24题解图② 由(Ⅰ)知 DM=EM, ∴∠DMN=∠EMN=1 2∠DME,DN=EN. 7分!! ∵∠B=45°,∠C=75°, ∴∠BAC=60°. 由(Ⅰ)知∠DME=2∠BAC=120°. ∴∠DMN=60°, 8分!!!!!!!!!!!! ∴DN=DM·sin∠DMN=槡3 2DM, ∴DE=2DN 槡= 3DM. 9分!!!!!!!!!! △MDE周长 =DM+ME+DE =DM+DM 槡+ 3DM =( 槡2+ 3)DM =( 槡2+ 3)×1 2AP. 10分!!!!! ∴当 AP最短时,△MDE的周长最小. 此时 AP⊥BC. 11分!!!!!!!!!!!!! 当 AP⊥BC时, ∵∠B=45°,∴AP=槡2 2AB=槡2 2 槡×6 2=6, ∴△MDE周长的最小值为( 槡2+ 3)×1 2×6=6+3 槡3. 12分!!!!!!!!!!!!!!!!! 25.(Ⅰ)证明:∵Δ=(-n)2 -4m(-m+n) =(n-2m)2≥0, 3分!!!!!! ∴该函数图象与 x轴必有交点; 4分!!!!!! (Ⅱ)解:(ⅰ)∵m-n=3, ∴n=m-3. ∴y1 =mx2 -nx-m+n=mx2 -(m-3)x-3. 当 y1 =0时,mx2 -(m-3)x-3=0, 解得 x1 =1,x2 =-3 m. 5分!!!!!!!!!! ∴二次函数图象与 x轴交点为(1,0)和(-3 m,0). ∵当 -m≤x<1时,二次函数的最大值小于 0, ∴ -3 m <-m<1. 7分!!!!!!!!!!!! 又∵m>0, ∴0<m 槡< 3; 8分!!!!!!!!!!!!!! (ⅱ)∵y2 =|mx2 -nx-m+n|,m-n=3, ∴当 x<-3 m或 x>1时,y2 =mx2 -(m-3)x-3, 当 -3 m≤x≤1时,y2 =-mx2 +(m-3)x+3. ∵当 -4<p<-1时,点 A在直线 y=-x+4的 上方, ∴当 -1<-3 m,即 m>3时,有 m×(-1)2 -(m-3)×(-1)-3≥ -(-1)+4, 10分!!!!!!!!!!!!!!!!! 解得 m≥11 2. 11分!!!!!!!!!!!!! 当 -3 m <-4,即 m<3 4时,有 -m×(-1)2 +(m-3)×(-1)+3≥ -(-1)+4 且 -m×(-4)2 +(m-3)×(-4)+3≥ -(-4)+ 4, 13分!!!!!!!!!!!!!!!!!! ∴m≤ 7 20. 又∵m>0, ∴0<m≤ 7 20. 综上所述,m的取值范围为 0<m≤ 7 20或 m≥11 2. 14分 ! !!!!!!!!!!!!!!!!! 63 2019年南平市初中毕业班适应性检测 数学试题参考答案及评分说明 第Ⅰ卷 一、选择题(本大题共 10小题,每小题 4分,共 40分) 1.A 【解析】由非零实数 a的相反数为 -a,得 6的相 反数为 -6. 2.B 【解析】逐项分析如下: 选项 逐项分析 正误 A 三角形既不是轴对称图形,也不是 中心对称图形 B 菱形既是轴对称图形,又是中心对 称图形 √ C 角是轴对称图形,但不是中心对称 图形 D 平行四边形是中心对称图形,但不 是轴对称图形 3.C 【解析】将一个大于 10的数用科学记数法表示为 a×10n的形式,其中 1≤a<10,∴a=1.5,n为正整 数,且等于原数的整数位数减 1,∴n=11-1=10,∴ 15000000000=1.5×1010. 4.D 【解 析】由 圆 周 角 定 理 可 知 ∠AOB=2∠ACB =68°. 5.A 【解析】∵正放表示整数,斜放表示负数,∴图② 中所得的数值为 2+(-4)=-2. 6.B 【解析】A.此项调查具有破坏性,应使用抽样调 查,故 A错误;B.众数是一组数据出现次数最多的 数,6出现了 2次,出现次数最多,则这组数据的众数 为 6,故 B正确;C.∵随机抽取 200名学生进行调 查,∴样本容量为 200,故 C错误;D.∵甲、乙两人射 击的平均数相同,且 s2 甲 <s2 乙 ,∴甲的成绩更稳定,故 D错误. 7.C 【解析】∵AB∥CD,∴∠CFE=∠AEM=50°,∴ ∠DFN=∠CFE=50°. 8.C 【解析】由题意可得△BCE≌△ACD,∴∠CBE= ∠CAD,∵ △ABC是 等 腰 直 角 三 角 形,∴ ∠CBA= ∠CAB=45°,∵ ∠DAB=10°,∴ ∠CAD=∠CAB- ∠DAB=35°,∴∠ABE=∠CBE+∠CBA=∠CAD+ ∠CBA=80°. 9.A 【解析】∵甲型机器人每小时搬运 x千克,∴乙型 机器人每小时搬运(x+30)千克,由题意可得600 x = 800 x+30. 10.A 【解析】如解图,过点 A作 AF⊥BC于点 F,过点 第 10题解图 E作 EG⊥ BC于 点 G,∴ EG∥ AF,∴ △CEG∽ △CAF,∵ AE= 2CE,∴AC=3CE,∵AF⊥BC,AB =AC,∴CF=BF=3,∴CG=1 3 CF=1,∵BD=DE=y,∴DG=5 -y,在 Rt△DEG中,由勾 股 定 理得 DG2 +EG2 = DE2,即(5-y)2 +EG2 =y2,解得 y=1 10EG2 +5 2,∵ x=S△ABC =1 2BC·AF=1 2×6×3EG=9EG,∴EG= 1 9x,∴y=1 10×(1 9x)2 +5 2= 1 810x2 +5 2. 第Ⅱ卷 二、填空题(本大题共 6小题,每小题 4分,共 24分) 11.x(x+1) 12.槡5(答案不唯一) 【解析】设无理数为 a,∵1<a< 3,∴1<a2 <9,∴a2 可取 5,∴a 槡= 5.(答案不唯一, 满足 1<a2 <9即可) 13.6 【解析】由多边形内角和定理 180°×(n-2)= 720°,解得 n=6. 14.16π 【解析】∵l扇形 =nπ×8 180 =4π,解得 n=90,∴ 此扇形的面积为 S=90π×82 360 =16π. 15.n+1 【解析】当 n为奇数时,中位数为从大到小排 列后第n+1 2 个数,第n+1 2 个数为 n+1;当 n为偶数 时,∵共有 n个数据,∴中位数应为将数据从小到 大排列后第 n 2个数和第 n 2+1个数的平均数,由题 意可知,第 n 2个数为 n,第 n 2+1个数为 n+2,此时 中位数为n+n+2 2 =n+1,∴这组数据的中位数为 n +1. 16.65 9 【解析】要使 EO与线段 BC有交点,且使 AD最 小,故当⊙O与 BC相切时,AD最小,如解图,∵⊙O 与 BC相切,∴∠OEB=90°,∵∠ACB=90°,∴OE ∥AC,∴△BOE∽△BAC,∴OE AC=OB AB,在 Rt△ABC 中,∵AC=5,BC=12,∴AB=13,设 OE=x,则 OA= OE=x,∴OB=13-x,∴ x 5=13-x 13 ,解得 x=65 18, ∴ 73 AD=2x=65 9. 第 16题解图 三、解答题(本大题共 9小题,共 86分) 17.解:原式 =2×1 2 槡-1+ 3-1+2 4分!!!!! 槡=1-1+ 3-1+2, 6分!!!!!!! 槡= 3+1. 8分!!!!!!!!!!!! 18.解:由①得,2x-4<x-2, 2分!!!!!!!! 解得 x<2, 3分!!!!!!!!!!!!!! 由②得,x>-1, 6分!!!!!!!!!!!! ∴不等式组的解集是 -1<x<2. 8分!!!!! 19.证明:∵四边形 ABCD是平行四边形, ∴OA=OC,OB=OD. 2分!!!!!!!!! 又∵E,F,G,H分别是 AO,BO,CO,DO的中点, ∴OE=1 2OA,OG=1 2OC,OF=1 2OB,OH=1 2OD. 4分!!!!!!!!!!!!!!!!!! ∴OE=OG,OF=OH. 6分!!!!!!!!!! ∴四边形 EFGH是平行四边形. 8分!!!!!! 20.解:(1)144, 2分!!!!!!!!!!!!!! 补全条形统计图如解图①: 各年级参赛读后感篇数条形统计图 第 20题解图① 4分!!!!!!!!!!!!!!!!!!! (2)设获特等奖 4篇读后感编号为 A,B,C,D,其中 七年级获特等奖读后感为 A,依题意, 方法一:列举所有可能结果如下: A B C D A (A,B) (A,C) (A,D) B (B,A) (B,C) (B,D) C (C,A) (C,B) (C,D) D (D,A) (D,B) (D,C) 6分!!!!!!!!!!!!!!!!!!! 方法二:画树状图如下: 第 20题解图② 6分!!!!!!!!!!!!!!!!!!! 由列表(树状图)知,一共有 12种等可能的情况,而 七年级特等奖读后感被广播电台播出的情况有 6种, ∴P(七年级特等奖读后感被广播电台播出)=6 12 =1 2. 8分!!!!!!!!!!!!!!!! 21.(1)证明:∵AE∥BF, ∴∠EAC=∠ACB. 2分!!!!!!!!!!! 又∵AC平分∠BAE, ∴∠BAC=∠EAC. 3分!!!!!!!!!!! ∴∠BAC=∠ACB. 4分!!!!!!!!!!! ∴AB=BC; 5分!!!!!!!!!!!!!! (2)解:作图如解图: 第 21题解图 8分!!!!!!!!!!!!!!!!!!! 22.解:(1)由点 A(n,4),AB⊥x轴于点 B,且点 A在第 一象限内,得 AB=4,OB=n, ∴S△AOB =1 2AB·OB=1 2×4n=2n. 1分!!!! 由 S△AOB =2,得 n=1, 2分!!!!!!!!!! ∴A(1,4). 3分!!!!!!!!!!!!!! 把 A(1,4)代入 y=m x中,得 m=4; 4分!!!! (2)由直线 y=kx+2过点 A(1,4),得 k=2, 5分 !! !!!!!!!!!!!!!!!!!! ∴一次函数的解析式为 y=2x+2. 6分!!!! 令 y=0,得 x=-1, ∴点 C的坐标为(-1,0). 7分 !!!!!!!! 83 由(1)可知 OB=1,∴BC=2. 8分!!!!!!! 在 Rt△ABC中,AC= AB2 +BC槡 2 = 42 +2槡 2 =2 槡5. 10分!!!!!!!!!!!!!!!!! 23.解:设商品 A每件原价 x元,商品 B每件原价 y元, 依题意,得 60x+30y=1080, 50x+10y=840{ , 4分!!!!!!!!!!! 解得 x=16, y=4{ , 8分!!!!!!!!!!!!! 则买 500件 A商品和 500件 B商品打折前后相差: 500×16+500×4-9600=400(元), 9分!!!! 答:打折后买 500件 A商品和 500件 B商品比不打 折少花了 400元. 10分!!!!!!!!!!! 24.(1)证明:∵OA⊥OE, ∴∠AOE=90°. 1分!!!!!!!!!!!! 又∵AB是⊙O的切线,OA是⊙O的半径, ∴OA⊥AB. ∴∠OAB=90°. 2分!!!!!!!!!!!! ∴∠AOE+∠OAB=180°. ∴OE∥AB; 3分!!!!!!!!!!!!!! 第 24题解图① (2)解:如解图①,过点 O作 OC⊥ AF于点 C, 4分!!!!!!! ∴AF=2AC,∠OCA=90°. 5分 !!! !!!!!!!!!! ∴∠AOC+∠OAC =90°. 又∵OA⊥AB, ∴∠OAC+∠CAB =90°. ∴∠AOC=∠CAB. 6分!!!!!!!!!!! 又∵BQ⊥AF, ∴∠AQB=90°. ∴∠ACO=∠AQB. 又∵OA=AB, ∴△AOC≌△BAQ(AAS). 7分!!!!!!!! ∴AC=BQ. ∴AF=2AC=2BQ. 即AF BQ=2; 8分!!!!!!!!!!!!!!! (3)解:如解图②,过点 O作 OC⊥AF于点 C, 由(2)得∠AOC =∠PAB, ∴cos∠AOC=cos∠PAB=4 5. 第 24题解图② 在 Rt△AOC中,OA=2, ∴OC =OA·cos∠AOC=2×4 5 =8 5, 9分!!!!!!!!! 又∵OA=OF,OC⊥AF于点 C, ∴∠COF=1 2∠AOF. 10分!!!!!!!!! 又∵OP平分∠EOF, ∴∠POF=1 2∠EOF, ∴∠POC=∠COF+∠POF=1 2∠AOF+1 2∠EOF =1 2∠EOA=45°. ∴△POC为等腰直角三角形. 11分!!!!!! ∴OP 槡= 2OC=8 5槡2. 12分!!!!!!!!!! 25.解:(1)∵m,n分别是关于 x的一元二次方程 ax2 + bx+c=a与 ax2 +bx+c=b的一个根, ∴ am2 +bm+c=a ① an2 +bn+c=b{ ② (), 2分!!!!!! 由 m=n+1,m=2得 n=1, 把 n=1,m=2,a=-1,代入()得, -4+2b+c=-1, -1+b+c=b{ , 4分!!!!!!!!!!! 解得 b=1, c=1{ , 即 b的值为 1,c的值为 1; 5分!!!!!!!! (2)由(1)的方程组()中① -②,得 a(m2 -n2)+b(m-n)=a-b, 6分!!!!!! (m-n)[a(m+n)+b]=a-b, 7分!!!!!! 由 m=n+1,得 m-n=1, 故 a(m+n)+b=a-b, 8分!!!!!!!!! ∴a(2n+1)+b=a-b, 即 b=-na; 9分!!!!!!!!!!!!!! (3)把 b=-na代入方程组()中②,得 c=-na, 10分!!!!!!!!!!!!!!! 由 b+c≥2a得 -2na≥2a, 当 a<0时,n≥ -1, 由 n≤ -1 2得,-1≤n≤ -1 2, 11分!!!!!! 由 b2 -4ac=a,且 b=c=-na,得 (-na)2 -4a·(-na)=a, 整理得,n2a2 +4na2 =a, ∵a<0, ∴ 1 a=n2 +4n, 即 1 a=(n+2)2 -4, 12分 !!!!!!!!!! 93 由于 1 a在 -1≤n≤ -1 2时随 n的增大而增大, 13分 ! !!!!!!!!!!!!!!!!! ∴当 n=-1时,a=-1 3,当 n=-1 2时,a=-4 7, 即 -4 7≤a≤ -1 3. 14分 !!!!!!!!!! 04查看更多