第4章 第3节 光的折射-2021年初中物理竞赛及自主招生大揭秘专题突破

第4章 第3节 光的折射-2021年初中物理竞赛及自主招生大揭秘专题突破

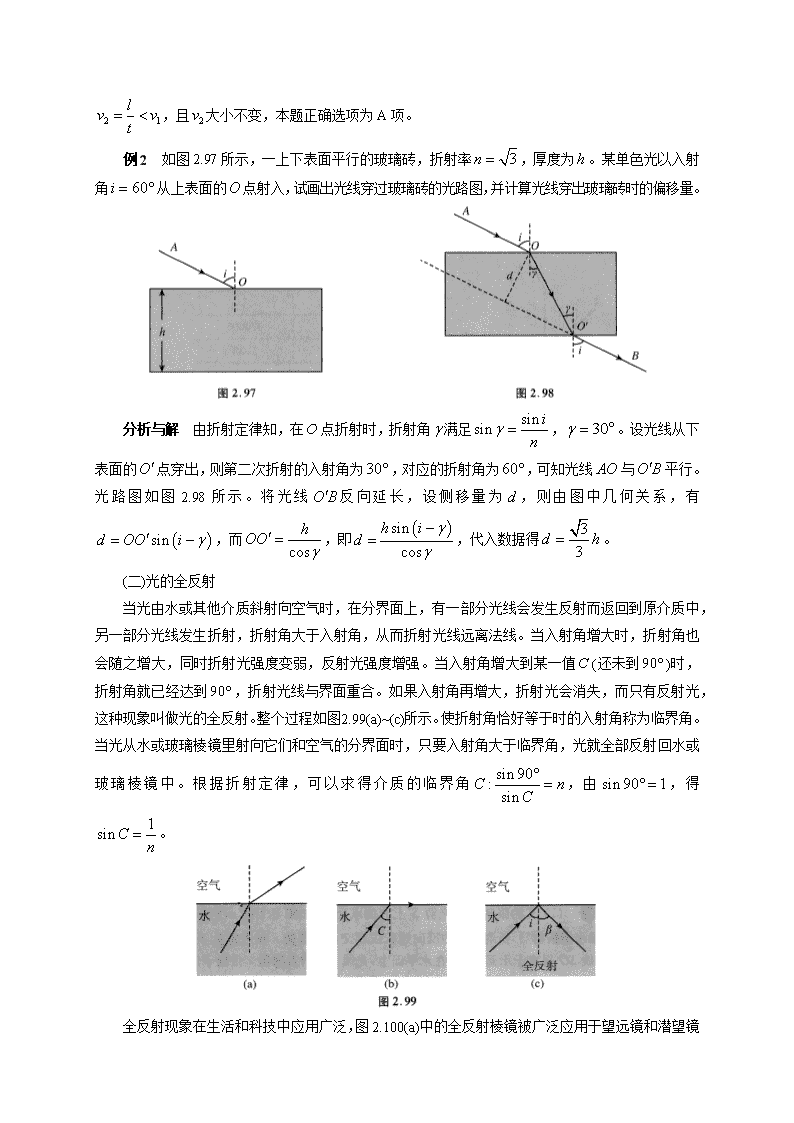
第三节 光的折射 当光由一种介质斜射入另一种介质中时，光的传播路径发生偏折的现象叫做光的折射。光的折 射遵从折射定律，它由荷兰物理学家斯涅耳发现。 (一)折射定律 如图 2.94 所示，在光的折射现象中，折射光线、入射光线和法线在同一平面内；折射光线和人 射光线分居法线两侧；当光从真空斜射入其他介质时，入射角i 与折射角 满足 sin sin i n  ，式中 n 叫 做介质的折射率。一般说来，介质的折射率只与介质种类有关。表 2.1 给出了几种介质对光的折射 率。 表 2.1 介质 折射率 真空 1 空气 1.0003 水 1.33 玻璃 1.4~1.9 酒精 1.36 冰 1.309 折射率反映了介质对光折射本领的强弱，折射率越大，介质对光的折射能力越强。同一介质对 各种色光的折射率并不相同，红光的折射率最小，紫光的折射率最大，这也是白光通过三棱镜后能 发生色散的原因。表 2.1 实际上给出的是各种介质对黄光的折射率。由于空气的折射率非常接近于 真空，空气的折射率也往往被认为等于 1。 例1 如图2.95所示，水池的宽度为 L ，在水池右侧距离池底高度为 H 处有一激光束，水池内无水时恰好在水池的左下角产生一个光斑。已知 L H ，现向水池内注水，水面匀速上升，则光斑( )。 A．匀速向右移动，且移动速度小于水面上升的速度 B．匀速向右移动，且移动速度大于水面上升的速度 C．减速向右移动，但速度始终大于水面上升的速度 D．加速向右移动，但速度始终小于水面上升的速度 分析与解 如图 2.96 所示，设经过时间t ，水面匀速上升的高度为 d ， 则水面上升的速度为 1 dv t  ，此时光斑由 A 点移动到 P 点，设入射角为i ， 折射角为 ，则由几何关系可知 AP 长度为  tan tanl d i   ，因为图中 L H ，所以 45i   ，因此  1 tanl d   d ，则光斑的速度 2 1 lv vt   ，且 2v 大小不变，本题 正确选项为 A 项。 例 2 如图 2.97 所示，一上下表面平行的玻璃砖，折射率 3n  ，厚度为 h 。某单色光以入射 角 60i   从上表面的 O 点射入，试画出光线穿过玻璃砖的光路图，并计算光线穿出玻璃砖时的偏移量。 分析与解 由折射定律知，在O 点折射时，折射角 满足 sinsin i n   ， 30   。设光线从下 表面的O 点穿出，则第二次折射的入射角为30 ，对应的折射角为 60 ，可知光线 AO 与O B 平行。 光 路 图 如 图 2.98 所 示 。 将 光 线 O B 反 向 延 长 ， 设 侧 移 量 为 d ， 则 由 图 中 几 何 关 系 ， 有  sind OO i   ，而 cos hOO    ，即  sin cos h id    ，代入数据得 3 3d h 。 (二)光的全反射 当光由水或其他介质斜射向空气时，在分界面上，有一部分光线会发生反射而返回到原介质中， 另一部分光线发生折射，折射角大于入射角，从而折射光线远离法线。当入射角增大时，折射角也 会随之增大，同时折射光强度变弱，反射光强度增强。当入射角增大到某一值 C (还未到 90 )时， 折射角就已经达到90 ，折射光线与界面重合。如果入射角再增大，折射光会消失，而只有反射光， 这种现象叫做光的全反射。整个过程如图2.99(a)~(c)所示。使折射角恰好等于时的入射角称为临界角。 当光从水或玻璃棱镜里射向它们和空气的分界面时，只要入射角大于临界角，光就全部反射回水或 玻璃棱镜中。根据折射定律，可以求得介质的临界角 sin90: sinC nC   ，由sin90 1  ，得 1sin C n  。 全反射现象在生活和科技中应用广泛，图 2.100(a)中的全反射棱镜被广泛应用于望远镜和潜望镜 中；图 2.100(b)是光导纤维中光的全反射现象。光导纤维是很细的玻璃丝，外表涂有很薄的另一种材 料的涂层，光在分界面上发生全反射。光导纤维制成的光缆以光速传递信号，质量和信息量都远远 超过了用金属做成的电缆。 例 3 (上海第 25 届大同杯初赛)如图 2.101 所示，只含红光和紫光的复色光束 PO ，沿半径方向 射入空气中的玻璃半圆柱后，如果只被分成 OA 和OB 两光束沿图示方向射 出，则( )。 A．OA 为红光， OB 为紫光 B． OA 为紫光，OB 为红光 C． OA 为红光，OB 为复色光 D．OA 为紫光， OB 为复色光 分析与解 复色光从空气沿着半径(法线)方向进入半圆柱时，光线的传播路径不发生偏折，但当 光线从半圆柱下表面射向空气时，将发生折射。由于紫光和红光的折射率不同，因此红光和紫光的 折射光线不会重合，而折射光线只有 OA 一条，可以肯定一定有一种色光发生了全发射。根据全反 射的规律，全反射时的临界角满足 1sin C n  ，由于紫光的折射率大于红光的折射率，因此紫光对应 的临界角较小，可知紫光发生全反射，光线 OA 为红光。考虑到红光会同时发生反射，因此OB 为 红光和紫光的复色光，本题正确选项为 C 项。 例4 如图2.102所示，水面下距水面 h 处有一盏灯 S (可视为点光源)，现人在岸上看水中的灯： (1)人在光源 S 正上方的水面上观察光源 S ，感觉到 S 深度为多少？ (已知 0  时，sin tan  ) (2)人发现该灯只能照亮水面上的一个圆形区域，已知水的折射率为 n 求水面被点光源照亮的圆形区域的面积。 分析与解 (1)人的眼睛位于光源 S 上方的水面处，如图2.103(a)所示。从光源 S 发出的光线经 水面折射后，折射光线的反向延长线相交而成虚像。现考察从 S 发出的两条光线，其中光线 SO 垂 直于水面， O 点在水平面上，光线 SO 的入射角i 接近于零，对应的折射角为 ，折射光线反向延 长与 SO 交于像点 S ，则由几何关系知 tanOO h i  ，像深度 h 满足 tanOO h   ，由折射定律 sin sin ni   ，结合 0  时，sin tan  ，有 tan tan ih h   sin sin i hh n  。可见像的位置变高了。 (2)从光源 S 发出的光线，经水面折射至空气中时，人觉得该处水面有亮光，当光线的入射角较 大，发生全反射时，没有光线透出水面，该处水面较暗。设光线由水斜射入空气时发生全反射的临 界角为C ，如图 2.103(b)所示，光线 SP 恰发生全反射，则以O 为圆心，以OP 为半径的圆内，皆有 光线透出水面，形成亮光区域。由光的折射定律 1sin C n  ，圆半径 2 tan 1 hR h C n    ，所以点 光源能照亮水面的圆形面积 2 2 2 1 hS R n   面积 。 从以上几例可以看出，在应用反射定律处理光的折射和全反射类问题时，要注意画出光线的传 播路线，充分运用图中的几何关系，结合直角三角形知识求解。 (三)光速与折射率的关系 任何色光在真空中传播的速度都是光速，真空中的光速为 83.0 10 m / sc   。但是在其他透明 介质中，光的传播速度小于真空中的光速。设光在介质中传播速度为 v ，介质的折射率为 n ，则有 cn v  ，即介质对某色光的折射率等于光在真空中的传播速度与该色光在介质中传播速度之比。 在可见光当中，介质对红光的折射率最小，对紫光的折射率最大，因此可知，在同一介质中， 红光的传播速度大于紫光的传播速度。水的折射率为 4 3 ，因此光在水中的传播速度为真空中光速的 3 4 。 例5 (上海第29届大同杯复赛)一束复色光由空气射向玻璃，发生折射而分为 a ，b 两束单色光， 其传播方向如图2.104所示。设玻璃对 a ，b 的折射率分别为 an ， bn ，且 a ，b 在玻璃中的传播速度 分别为 av ， bv ，则 an ________ bn ， av ________ bv (均选填“>“<”或“=”) 分析与解 由题图可知，在入射角相同的情况下，a 色光的折射角较小， 因此玻璃对 a 色光的折射率较大，即 a bn n ，又根据光在介质中的光速 cv n  ，折射率越大，在介质中的光速越小，有 a bv v 。 练习题 1．(上海第 9 届大同杯初赛)下面表示光线通过半圆形玻璃砖的光路图中正确的是( )。 A B C D 2．(上海第 7 届大同杯初赛)光从一个盛有水的薄壁玻璃水缸射出，经过空气后射入另一个盛有 水的薄壁玻璃水缸，若不考虑玻璃水缸壁对光的折射影响，下图中正确反映光路的是( )。 A B C D 3．(上海第 12 届大同杯初赛)在一块玻璃砖上挖去一块半圆形的玻璃，如有一条通过圆心的光线 射到该玻璃砖上，则正确的光路图为( )。 A B C D 4．(上海第26届大同杯初赛)地球的自转让我们每天能看到日出和日落现象，若地球表面不存在 大气层(假设)，则日出和日落时间相比现在( )。 A．日出提前，日落推迟 B．日出推迟，日落提前 C．日出和日落都会提前 D．日出和日落都会推迟 5．(上海第 26 届大同杯初赛)如图 2.105 所示，两个并排而且深度相同的水池，一个装水，另一 个未装水，在两池的中央各竖立一支长度相同而且比池深略长的标杆。此时，阳光斜射到水池，下 列关于两水池中标杆影子的说法中，正确的是( )。 A．装水的池中标杆影子较长 B．未装水的池中标杆影子较长 C．两池中标杆影子长度相同 D．装水的池中标杆没有影子 6．如图 2.106 所示，在 P 点有一发光物体，则在水下观察者的眼里，该物 体的像位于( )。 A． P 点以上 B． P 点以下 C． P 点 D． P 点左上方 7．(上海第25届大同杯复赛)潜泳的人从水下向上看，会看到一彩色镶边、内有图像的圆面，那 么( )。 A．圆面内只能呈现水面上的部分景物 B． 彩色镶边是由于水面四周各种物体的颜色所引起的 C．彩色镶边是由于不同颜色的光折射程度略有不同所致 D．圆面中图像呈现的是水面外的景物，且看到景物的高度比实际景物要低 8．(上海第 22 届大同杯初赛)如图 2.107 所示，平行玻璃砖的厚度为 d 。一束单色光斜射到玻璃 砖的上表面，入射角为 ，折射角为  ，光线从玻璃砖的下表面射出，则出 射光线与入射光线的距离 x 为( )。 A．  sin cos d     B． sin cos d   C．  sin sin d     D． sin sin d   9．(上海第 2 届大同杯初赛)一柱形物体直立在平静、清澈的水面上空静止不动。位于水中C 点 的观察者正好看到了这一柱形物体所成的像，如图 2.108 所示。那么，他看到的可能是( )。 A．与物体原来位置相同、大小一样的像 B．与物体位于同一位置，大小一样、倒立的像 C．在 ab 右上方、倾斜的像 D．在 ab 左上方、倾斜的像 E．在 ab 正左方、正立的像 F．在 ab 正左方、倒立的像 G．在 ab 正下方、倒立的像 10．(上海第 4 届大同杯初赛)根据图 2.109 所示的光线在玻璃、水、空气三种物质中折射的情况， 可以断定这三种物质依次是( )。 A．①玻璃，②空气，③水 B．①空气，②水，③玻璃 C．①空气，②玻璃，③水 D．①玻璃，②水；③空气 11．(上海第 15 届大同杯初赛)在光学中，折射率是这样定义的：让光线从真空(空气)射入某介 质发生折射，如果入射角是i ，折射角是 ，则该介质的折射率为 sin sin in  。图 2.110 为某光线通过 三棱镜(等腰三角形的顶角为 2 )的光路图，则该三棱镜的折射率为( )。 A． tan B． cot C． tan 2 D． cot 2 12．(上海第 16 届大同杯初赛)图 2.111 是一个半径为10cm 的均匀透明球，一束光由球面 A 点 射入，从球面 B 点射出，光的传播方向改变了30 ，已知入射光线与半径OA 的夹角为 75 ，则该 光线在球内传播的路径长度为( )。 A．10cm B．10 2cm C．10 3cm D． 20cm 13．(上海第 9 届大同杯复赛)如图 2.112 所示，入射光线 SO 以 45的入射角从空气射入两面平 行的玻璃砖中，折射角为32 ，玻璃砖的CD 面上镀有不透明的反光金属薄膜。则下列说法中正确 的是( )。 A．光线经CD 面反射后循原路返回 B．光线经CD 面反射后从 AB 面上发生全反射 C．光线经CD 面反射后从 AB 面射出，折射角为 45 D．光线经CD 面反射后从 AB 面射出，折射角为32 14．(上海第 11 届大同杯复赛)一条光线通过在水中的球形空气泡，表示 出射光线的可能是图 2.113 中的( )。 A． a B．b C． c D． d 15．如图 2.114 所示，一束红光和一束蓝光平行射到一个三棱镜上，经折射后交于光屏上的点 M ， 若用 1n ， 2n 分别表示三棱镜对红光和蓝光的折射率，下列说法正确的是( )。 A． 1 2n n ， a 为红光，b 为蓝光 B． 1 2n n ， a 为蓝光，b 为红光 C． 1 2n n ， a 为红光，b 为蓝光 D． 1 2n n ， a 为蓝光，b 为红光 16．固定的半圆形玻璃砖横截面如图 2.115 所示，O 为圆心，OO 为 MN 的垂线，足够大的光 屏 PQ 紧靠玻璃砖右侧且垂直于 MN 。由 A ，B 两种单色光组成的一束光线沿着半径方向射向 O 点， 入射光线与OO 夹角 较小时，光屏 NQ 区域出现两个光斑，逐渐增大 角，当  时，光屏 NQ 区域 A 光的光斑消失，继续增大 角，当  时，光屏 NQ 区域 B 光的光斑消失，则( )。 A．玻璃砖对 A 光的折射率比对 B 光的大 B． A 光在玻璃中的传播速度比 B 光大 C．当    时，屏上 NQ 段只有一个光斑 D．当 90    时，屏上 NQ 段只有一个光斑 17．(上海第22届大同杯复赛)如图2.116所示，在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌 面接触，圆锥的轴(图中虚线)与桌面垂直，过轴线的截面为等边三角形。有一半径为 r 的圆柱形平行 光束垂直人射到圆锥的底面上，光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1.5，则光束在 桌面上形成的光斑半径为________，并在图中画出光路图。 18．图 2.117 所示是一种折射率 3n  的棱镜，用于某种光学仪器中。现有一束光线沿 MN 方 向射到棱镜的 AB 面上，入射角 60i   ，试画出此束光线进入棱镜后又射出棱镜的光路图(不考虑返 回到 AB 和 BC 面上的光线)，要求简要写出分析过程。 参考答案 1．A。光由空气斜射入玻璃时，折射角小于人射角，折射光线靠近法线；由玻璃斜射入空气时， 折射角大于入射角，折射光线远离法线；若光垂直于玻璃表面入射(即沿着半圆形玻璃砖的半径方向 入射)，光线不发生偏折。本题只有 A 项正确。 2．C。 3．A。 4．B。图 2.118 给出了日出和日落时太阳光斜射入大气层发 生偏折的情况。日出时，太阳还在地平线以下，地平线上 A 处的 人已经可以看到太阳发出的光了。若没有大气层，则太阳必须到 达地平线， A 处的人才能看到日出，因此若不存在大气层，日出 将推迟。日落时，太阳已经下降到地平面以下，但由于大气对光的折射，地平线上 A 处的人仍能看 到太阳，若没有大气层，则太阳到达地平线上时，人们就觉得已经日落了，日落将提前。 5．B。有水时，掠过杆顶端的光线由空气斜射人水中，折射光线向法线靠近，形成的影子长度 变短。 6．A。如图 2.119 所示，为了找到发光点 P 的像的位置，自 P 发出两条光 线 PA ， PB ， A ， B 分别为入射点；光线 PA 垂直于水面，光线 PB 入射角 趋近于零，将光线 PB 的折射角设为  ，水的折射率记为  1n n  ，则 sin sin n   。 将两个折光线反向延长，交于 P点，则 P点即为人眼看到的像。设 PA 的长度 为 h ， 则 在 直 角 PAB△ 中 可 得 tanAB h  ， 在 直 角 P AB△ 中 可 得 tan tan tan AB hP A       ， 考 虑 到  ，  趋 近 于 零 ， 则 tan tan hP A      sin sin h nh   。 7．C。如图 2.120 所示，从水面上各个方向入射的光线，均可折射后进入人眼，其中，紧贴着 水面入射的光线(入射角可视为 90 )折射角最大，对应的折射光线的反 向延长线方向如OA ，OB 所示，则人能看到水面上任何位置的景物， 且景物只出现在以 AOB 为锥角的锥形内，该锥形与水面相交的圆即 为题目所述的“有图像的圆面”。由于是从水底观察水面上的景物，所以 所看到的景物比实际景物要高。圆周围的彩色镶边实际是由于水对各种 色光折射程度不同引起的色散现象。 8．A。解析略，可参照本节例2。 9．C。可以根据光的折射规律分别画出从 a ，b 出发的两条光线，并将折射光线反向延长到 a ， b 的像。 10．A。光线从①斜射入②时，折射角大于入射角，则可知②相对于①是光疏介质(即①的折射 率大于②)，光从②斜射入③时，折射角小于入射角，则可知③相对于②是光密介质(即②的折射率小 于③)，因此 A 项符合题意。 11．B。作出光由空气斜射入三棱镜时的法线，可求得入射角为90  ，折射角为 ，则三楼 镜的折射率为  sin 90 cos cotsin sinn         。 12．A。如图 2.121 所示，将入射光线延长，并将出射光线反向延 长，两延长线交于 P 点，则 30DPB   ， 15PAB PBA     ， 则 75 15 60BAO       ， OAB△ 为等边三角形， AB 的长度等 于球的半径。 13．C。光线经CD 面反射后，反射角等于入射角，为32 ，然后再经 AB 面折射，折射时的入 射角等于32 ，折射角等于 45。 14．B。注意光在折射时入射角、折射角的大小关系。 15．B。红光的折射率小于蓝光的折射率，所以 1 2n n ，在穿过三棱镜的过程中，红光的偏折 程度小于蓝光，结合图2.114知 a 为蓝光，b 为红光，选项B正确。 16．AC。 角较小时， A ，B 两种色光由玻璃斜射入空气，发生折射照射在 NQ区域，逐渐增 大 角的过程中， A 光、 B 光由于先后发生全反射而返回到玻璃中，对应的光斑消失。由题可知 A 光对应的临界角 小于 B 光对应的临界角  ，由 1sin C n  ，可知折射率 A Bn n ，因此A选项正确。 折射率越大，光在介质中的传播速度越小，B选项错误。当    时，只有 A 色光发生全反射 而 B 色光折射后仍照射在 NQ区域，因此C选项正确。当 90    时，两种色光均已发生全反射， NQ 区域没有光斑，D选项错误。本题正确选项为AC。 17． 2r 。如图2.122所示，光线 PA 进入玻璃圆锥后，入射到 A 点，入射角为 60 ，由于 3 1 2sin60 2 3n     ，所以将发生全反射，且由几何关系，反射光线 AB 恰与圆锥侧面垂直， OAB△ 为等腰三角形，易得光斑的半径OB 为 2r 。 18．由折射率 sin60 sinn   ，得 AB 面上的折射角 30 = ° ，由几何关系得 BC 面上的入射角 45   ，全反射的临界角 1 2sin 23 C   ，光在 BC 面上发生全反射，此反射光线与 AC 面垂直。 光路图如图 2.123 所示。