2020年山东省济宁市中考数学试卷【含答案；word版本试题；可编辑】

2020年山东省济宁市中考数学试卷【含答案；word版本试题；可编辑】

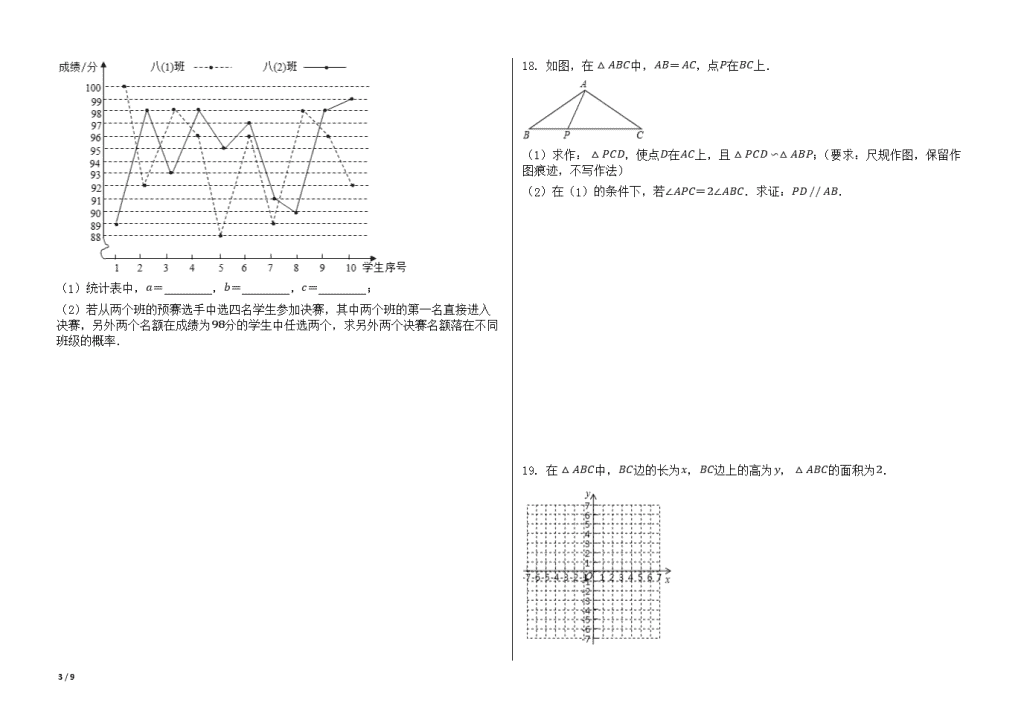
‎2020年山东省济宁市中考数学试卷 一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项符合题目要求．‎ ‎1. ‎-‎‎7‎‎2‎的相反数是（ ）‎ A.‎-‎‎7‎‎2‎ B.‎-‎‎2‎‎7‎ C.‎2‎‎7‎ D.‎‎7‎‎2‎ ‎2. 用四舍五入法将数‎3.14159‎精确到千分位的结果是（ ）‎ A.‎3.1‎ B.‎3.14‎ C.‎3.142‎ D.‎‎3.141‎ ‎3. 下列各式是最简二次根式的是（ ）‎ A.‎13‎ B.‎12‎ C.a‎3‎ D.‎‎5‎‎3‎ ‎4. 若一个多边形的内角和等于‎1080‎‎∘‎，则这个多边形的边数是(        )‎ A.‎9‎ B.‎8‎ C.‎7‎ D.‎‎6‎ ‎5. 一条船从海岛A出发，以‎15‎海里/时的速度向正北航行，‎2‎小时后到达海岛B处．灯塔C在海岛A的北偏西‎42‎‎∘‎方向上，在海岛B的北偏西‎84‎‎∘‎方向上．则海岛B到灯塔C的距离是（ ）‎ A.‎15‎海里 B.‎20‎海里 C.‎30‎海里 D.‎60‎海里 ‎6. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩（单位：cm）的平均数和方差，要从中选择一名成绩较高且发挥稳定的运动员参加决赛，最合适的运动员是（ ）‎ 甲 乙 丙 丁 平均数x‎¯‎ ‎376‎ ‎350‎ ‎376‎ ‎350‎ 方差s‎2‎ ‎12.5‎ ‎13.5‎ ‎2.4‎ ‎5.4‎ A.甲 B.乙 C.丙 D.丁 ‎7. 数形结合是解决数学问题常用的思想方法．如图，直线y＝x+5‎和直线y＝ax+b相交于点P，根据图象可知，方程x+5‎＝ax+b的解是（ ）‎ A.x＝‎20‎ B.x＝‎5‎ C.x＝‎25‎ D.x＝‎‎15‎ ‎8. 如图是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积是（ ）‎ A.‎12πcm‎2‎ B.‎15πcm‎2‎ C.‎24πcm‎2‎ D.‎‎30πcm‎2‎ ‎9. 如图，在‎△ABC中，点D为‎△ABC的内心，‎∠A＝‎60‎‎∘‎，CD＝‎2‎，BD＝‎4‎．则‎△DBC的面积是（ ）‎ A.‎4‎‎3‎ B.‎2‎‎3‎ C.‎2‎ D.‎‎4‎ ‎10. 小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案（如图所示），每个图案中他只在最下面的正方体上写“心”字，寓意“不忘初心”．其中第（1）个图案中有‎1‎个正方体，第（2）个图案中有‎3‎个正方体，第（3）个图案中有‎6‎个正方体，…按照此规律，从第‎(100)‎个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是（ ）‎ ‎ 9 / 9‎ A.‎1‎‎100‎ B.‎1‎‎20‎ C.‎1‎‎101‎ D.‎‎2‎‎101‎ 二、填空题：本大题共5小题，每小题3分，共15分．‎ ‎11. 分解因式a‎3‎‎-4a的结果是________．‎ ‎12. 已知三角形的两边长分别为‎3‎和‎6‎，则这个三角形的第三边长可以是________．‎ ‎13. 已如m+n＝‎-3‎，则分式m+nm‎÷(‎-m‎2‎-‎n‎2‎m-2n)‎的值是________．‎ ‎14. 如图，小明在距离地面‎30‎米的P处测得A处的俯角为‎15‎‎∘‎，B处的俯角为‎60‎‎∘‎．若斜面坡度为‎1:‎‎3‎，则斜坡AB的长是________米．‎ ‎15. 如图，在四边形ABCD中，以AB为直径的半圆O经过点C，D．AC与BD相交于点E，CD‎2‎＝CE⋅CA，分别延长AB，DC相交于点P，PB＝BO，CD＝‎2‎‎2‎．则BO的长是________．‎ 三、解答题：本大题共7小题，共55分．‎ ‎16. 先化简，再求值：‎(x+1)(x-1)+x(2-x)‎，其中x=‎‎1‎‎2‎．‎ ‎17. 某校举行了“防溺水”知识竞赛．八年级两个班各选派‎10‎名同学参加预赛，依据各参赛选手的成绩（均为整数）绘制了统计表和折线统计图（如图所示）．‎ 班级 八（1）班 八（2）班 最高分 ‎100‎ ‎99‎ 众数 a ‎98‎ 中位数 ‎96‎ b 平均数 c ‎94.8‎ ‎ 9 / 9‎ ‎（1）统计表中，a＝________，b＝________，c＝________；‎ ‎（2）若从两个班的预赛选手中选四名学生参加决赛，其中两个班的第一名直接进入决赛，另外两个名额在成绩为‎98‎分的学生中任选两个，求另外两个决赛名额落在不同班级的概率．‎ ‎18. 如图，在‎△ABC中，AB＝AC，点P在BC上．‎ ‎（1）求作：‎△PCD，使点D在AC上，且‎△PCD∽△ABP；（要求：尺规作图，保留作图痕迹，不写作法）‎ ‎（2）在（1）的条件下，若‎∠APC＝‎2∠ABC．求证：PD // AB．‎ ‎19. 在‎△ABC中，BC边的长为x，BC边上的高为y，‎△ABC的面积为‎2‎．‎ ‎ 9 / 9‎ ‎（1）y关于x的函数关系式是________，x的取值范围是________；‎ ‎（2）在平面直角坐标系中画出该函数图象；‎ ‎（3）将直线y＝‎-x+3‎向上平移a(a>0)‎个单位长度后与上述函数图象有且只有一个交点，请求出此时a的值．‎ ‎20. 为加快复工复产，某企业需运输一批物资．据调查得知，‎2‎辆大货车与‎3‎辆小货车一次可以运输‎600‎箱；‎5‎辆大货车与‎6‎辆小货车一次可以运输‎1350‎箱．‎ ‎（1）求‎1‎辆大货车和‎1‎辆小货车一次可以分别运输多少箱物资；‎ ‎（2）计划用两种货车共‎12‎辆运输这批物资，每辆大货车一次需费用‎5000‎元，每辆小货车一次需费用‎3000‎元．若运输物资不少于‎1500‎箱，且总费用小于‎54000‎元．请你列出所有运输方案，并指出哪种方案所需费用最少．最少费用是多少？‎ ‎21. 我们把方程‎(x-m‎)‎‎2‎+(y-n‎)‎‎2‎＝r‎2‎称为圆心为‎(m, n)‎、半径长为r的圆的标准方程．例如，圆心为‎(1, -2)‎、半径长为‎3‎的圆的标准方程是‎(x-1‎)‎‎2‎+(y+2‎‎)‎‎2‎＝‎9‎．在平面直角坐标系中，‎⊙C与轴交于点A，B，且点B的坐标为‎(8, 0)‎，与y轴相切于点D(0, 4)‎，过点A，B，D的抛物线的顶点为E．‎ ‎（1）求‎⊙C的标准方程；‎ ‎（2）试判断直线AE与‎⊙C的位置关系，并说明理由．‎ ‎ 9 / 9‎ ‎22. 如图，在菱形ABCD中，AB＝AC，点E，F，G分别在边BC，CD上，BE＝CG，AF平分‎∠EAG，点H是线段AF上一动点（与点A不重合）．‎ ‎（1）求证：‎△AEH≅△AGH；‎ ‎（2）当AB＝‎12‎，BE＝‎4‎时．‎ ‎①求‎△DGH周长的最小值；‎ ‎②若点O是AC的中点，是否存在直线OH将‎△ACE分成三角形和四边形两部分，其中三角形的面积与四边形的面积比为‎1:3‎．若存在，请求出AHAF的值；若不存在，请说明理由．‎ ‎ 9 / 9‎ 参考答案与试题解析 ‎2020年山东省济宁市中考数学试卷 一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项符合题目要求．‎ ‎1.D ‎2.C ‎3.A ‎4.B ‎5.C ‎6.C ‎7.A ‎8.B ‎9.B ‎10.D 二、填空题：本大题共5小题，每小题3分，共15分．‎ ‎11.‎a(a+2)(a-2)‎ ‎12.‎‎4‎ ‎13.‎‎1‎‎3‎ ‎14.‎‎20‎‎3‎ ‎15.‎‎4‎ 三、解答题：本大题共7小题，共55分．‎ ‎16.原式＝‎x‎2‎‎-1+2x-‎x‎2‎ ‎＝‎2x-1‎，‎ 当x=‎‎1‎‎2‎时，‎ 原式＝‎2×‎1‎‎2‎-1‎＝‎0‎．‎ ‎17.‎96‎,‎96‎,‎‎94.5‎ 班学生为A‎1‎，A‎2‎，（1）班学生为B‎1‎，B‎2‎，B‎3‎，‎ 一共有‎20‎种等可能结果，其中‎2‎人来自不同班级共有‎12‎种，‎ 所以这两个人来自不同班级的概率是‎12‎‎20‎‎=‎‎3‎‎5‎ ‎18.如图：作出‎∠APD＝‎∠ABP，即可得到‎△PCD∽△ABP；‎ 证明：如图，∵ ‎∠APC＝‎2∠ABC，‎∠APD＝‎∠ABC，‎ ‎∴ ‎∠DPC＝‎‎∠ABC ‎∵ ∴ PD // AB．‎ ‎19.y=‎‎4‎x,‎x>0‎ 在平面直角坐标系中画出该函数图象如图所示；‎ 将直线y＝‎-x+3‎向上平移a(a>0)‎个单位长度后解析式为y＝‎-x+3+a，‎ 解y=-x+3+ay=‎‎4‎x‎ ‎，整理得，x‎2‎‎-(3+a)x+4‎＝‎0‎，‎ ‎∵ 平移后的直线与上述函数图象有且只有一个交点，‎ ‎∴ ‎△‎＝‎(3+a‎)‎‎2‎-16‎＝‎0‎，‎ 解得a＝‎1‎，a＝‎-7‎（不合题意舍去），‎ 故此时a的值为‎1‎．‎ ‎20.设‎1‎辆大货车一次运输x箱物资，‎1‎辆小货车一次运输y箱物资，‎ ‎ 9 / 9‎ 由题意可得：‎2x+3y=600‎‎5x+6y=1350‎‎ ‎，‎ 解得：x=150‎y=100‎‎ ‎，‎ 答：‎1‎辆大货车一次运输‎150‎箱物资，‎1‎辆小货车一次运输‎100‎箱物资，‎ 设有a辆大货车，‎(12-a)‎辆小货车，‎ 由题意可得：‎150a+100(12-a)≥1500‎‎5000a+3000(12-a)<54000‎‎ ‎，‎ ‎∴ ‎6≤a<9‎，‎ ‎∴ 整数a＝‎6‎，‎7‎，‎8‎；‎ 当有‎6‎辆大货车，‎6‎辆小货车时，费用＝‎5000×6+3000×6‎＝‎48000‎元，‎ 当有‎7‎辆大货车，‎5‎辆小货车时，费用＝‎5000×7+3000×5‎＝‎50000‎元，‎ 当有‎8‎辆大货车，‎4‎辆小货车时，费用＝‎5000×8+3000×4‎＝‎52000‎元，‎ ‎∵ ‎48000<50000<52000‎，‎ ‎∴ 当有‎6‎辆大货车，‎6‎辆小货车时，费用最小，最小费用为‎48000‎元．‎ ‎21.如图，连接CD，CB，过点C作CM⊥AB于M．设‎⊙C的半径为r．‎ ‎∵ 与y轴相切于点D(0, 4)‎，‎ ‎∴ CD⊥OD，‎ ‎∵ ‎∠CDO＝‎∠CMO＝‎∠DOM＝‎90‎‎∘‎，‎ ‎∴ 四边形ODCM是矩形，‎ ‎∴ CM＝OD＝‎4‎，CD＝OM＝r，‎ ‎∵ B(8, 0)‎，‎ ‎∴ OB＝‎8‎，‎ ‎∴ BM＝‎8-r，‎ 在Rt△CMB中，∵ BC‎2‎＝CM‎2‎+BM‎2‎，‎ ‎∴ r‎2‎＝‎4‎‎2‎‎+(8-r‎)‎‎2‎，‎ 解得r＝‎5‎，‎ ‎∴ C(5, 4)‎，‎ ‎∴ ‎⊙C的标准方程为‎(x-5‎)‎‎2‎+(y-4‎‎)‎‎2‎＝‎25‎．‎ 结论：AE是‎⊙C的切线．‎ 理由：连接AC，CE．‎ ‎∵ CM⊥AB，‎ ‎∴ AM＝BM＝‎3‎，‎ ‎∴ A(2, 0)‎，‎B(8, 0)‎ 设抛物线的解析式为y＝a(x-2)(x-8)‎，‎ 把D(0, 4)‎代入y＝a(x-2)(x-8)‎，可得a=‎‎1‎‎4‎，‎ ‎∴ 抛物线的解析式为y=‎1‎‎4‎(x-2)(x-8)=‎1‎‎4‎x‎2‎-‎5‎‎2‎x+4=‎1‎‎4‎(x-5‎)‎‎2‎-‎‎9‎‎4‎，‎ ‎∴ 抛物线的顶点E(5, -‎9‎‎4‎)‎，‎ ‎∵ AE=‎3‎‎2‎‎+(‎‎9‎‎4‎‎)‎‎2‎=‎‎15‎‎4‎，CE＝‎4+‎9‎‎4‎=‎‎25‎‎4‎，AC＝‎5‎，‎ ‎∴ EC‎2‎＝AC‎2‎+AE‎2‎，‎ ‎∴ ‎∠CAE＝‎90‎‎∘‎，‎ ‎∴ CA⊥AE，‎ ‎∴ AE是‎⊙C的切线．‎ ‎22.证明：∵ 四边形ABCD是菱形，‎ ‎∴ AB＝BC，‎ ‎∵ AB＝AC，‎ ‎∴ AB＝BC＝AC，‎ ‎∴ ‎△ABC是等边三角形，‎ ‎∴ ‎∠ABC＝‎60‎‎∘‎，‎ ‎∴ ‎∠BCD＝‎120‎‎∘‎，‎ ‎∵ AC是菱形ABCD的对角线，‎ ‎∴ ‎∠ACD=‎1‎‎2‎∠BCD＝‎60‎‎∘‎＝‎∠ABC，‎ ‎∵ BE＝CG，‎ ‎∴ ‎△ABE≅△ACG(SAS)‎，‎ ‎∴ AE＝AG，‎ ‎ 9 / 9‎ ‎∵ AF平分‎∠EAG，‎ ‎∴ ‎∠EAF＝‎∠GAF，‎ ‎∵ AH＝AH，‎ ‎∴ ‎△AEH≅△AGH(SAS)‎；‎ ‎①如图‎1‎，‎ 过点D作DM⊥BC交BC的延长线于M，连接DE，‎ ‎∵ AB＝‎12‎，BE＝‎4‎，‎ ‎∴ CG＝‎4‎，‎ ‎∴ CE＝DG＝‎12-4‎＝‎8‎，‎ 由（1）知，‎△AEH≅△AGH，‎ ‎∴ EH＝HG，‎ ‎∴ l‎△DGH＝DH+GH+DG＝DH+HE+8‎，‎ 要是‎△AEH的周长最小，则EH+DH最小，最小为DE，‎ 在Rt△DCM中，‎∠DCM＝‎180‎‎∘‎‎-‎‎120‎‎∘‎＝‎60‎‎∘‎，CD＝AB＝‎12‎，‎ ‎∴ CM＝‎6‎，‎ ‎∴ DM=‎3‎CM＝‎6‎‎3‎，‎ 在Rt△DME中，EM＝CE+CM＝‎14‎，‎ 根据勾股定理得，DE=EM‎2‎+DM‎2‎=‎14‎‎2‎‎+(6‎‎3‎‎)‎‎2‎=4‎‎19‎，‎ ‎∴ ‎△DGH周长的最小值为‎4‎19‎+8‎；‎ ‎②Ⅰ、当OH与线段AE相交时，交点记作点N，如图‎2‎，连接CN，‎ ‎∴ 点O是AC的中点，‎ ‎∴ S‎△AON＝S‎△CON‎=‎‎1‎‎2‎S‎△ACN，‎ ‎∵ 三角形的面积与四边形的面积比为‎1:3‎，‎ ‎∴ S‎△AONS‎△AEC‎=‎‎1‎‎4‎，‎ ‎∴ S‎△CEN＝S‎△ACN，‎ ‎∴ AN＝EN，‎ ‎∵ 点O是AC的中点，‎ ‎∴ ON // CE，‎ ‎∴ AHAF‎=‎‎1‎‎2‎；‎ Ⅱ、当OH与线段CE相交时，交点记作Q，如图‎3‎，‎ 连接AQ，FG，∵ 点O是AC的中点，‎ ‎∴ S‎△AOQ＝S‎△COQ‎=‎‎1‎‎2‎S‎△ACQ，‎ ‎∵ 三角形的面积与四边形的面积比为‎1:3‎，‎ ‎∴ S‎△COQS‎△ACE‎=‎‎1‎‎4‎，‎ ‎∴ S‎△AEQ＝S‎△ACQ，‎ ‎∴ CQ＝EQ=‎1‎‎2‎CE=‎1‎‎2‎(12-4)‎＝‎4‎，‎ ‎∵ 点O是AC的中点，‎ ‎∴ OQ // AE，设FQ＝x，‎ ‎∴ EF＝EQ+FQ＝‎4+x，CF＝CQ-FQ＝‎4-x，‎ 由（1）知，AE＝AG，‎ ‎∵ AF是‎∠EAG的角平分线，‎ ‎∴ ‎∠EAF＝‎∠GAF，‎ ‎∵ AF＝AF，‎ ‎∴ ‎△AEF≅△AGF(SAS)‎，‎ ‎∴ FG＝EF＝‎4+x，‎ 过点G作GP⊥BC交BC的延长线于P，‎ 在Rt△CPG中，‎∠PCG＝‎60‎‎∘‎，CG＝‎4‎，‎ ‎∴ CP=‎1‎‎2‎CG＝‎2‎，PG=‎3‎CP＝‎2‎‎3‎，‎ ‎∴ PF＝CF+CP＝‎4-x+2‎＝‎6-x，‎ 在Rt△FPG中，根据勾股定理得，PF‎2‎+PG‎2‎＝FG‎2‎，‎ ‎ 9 / 9‎ ‎∴ ‎(6-x‎)‎‎2‎+(2‎‎3‎‎)‎‎2‎＝‎(4+x‎)‎‎2‎，‎ ‎∴ x=‎‎8‎‎5‎，‎ ‎∴ FQ=‎‎8‎‎5‎，EF＝‎4+‎8‎‎5‎=‎‎28‎‎5‎，‎ ‎∵ OQ // AE，‎ ‎∴ AHAF‎=EQEF=‎4‎‎28‎‎5‎=‎‎5‎‎7‎，‎ 即AHAF的值为‎1‎‎2‎或‎5‎‎7‎．‎ ‎ 9 / 9‎