平行四边形(1)教案1

平行四边形(1)教案1

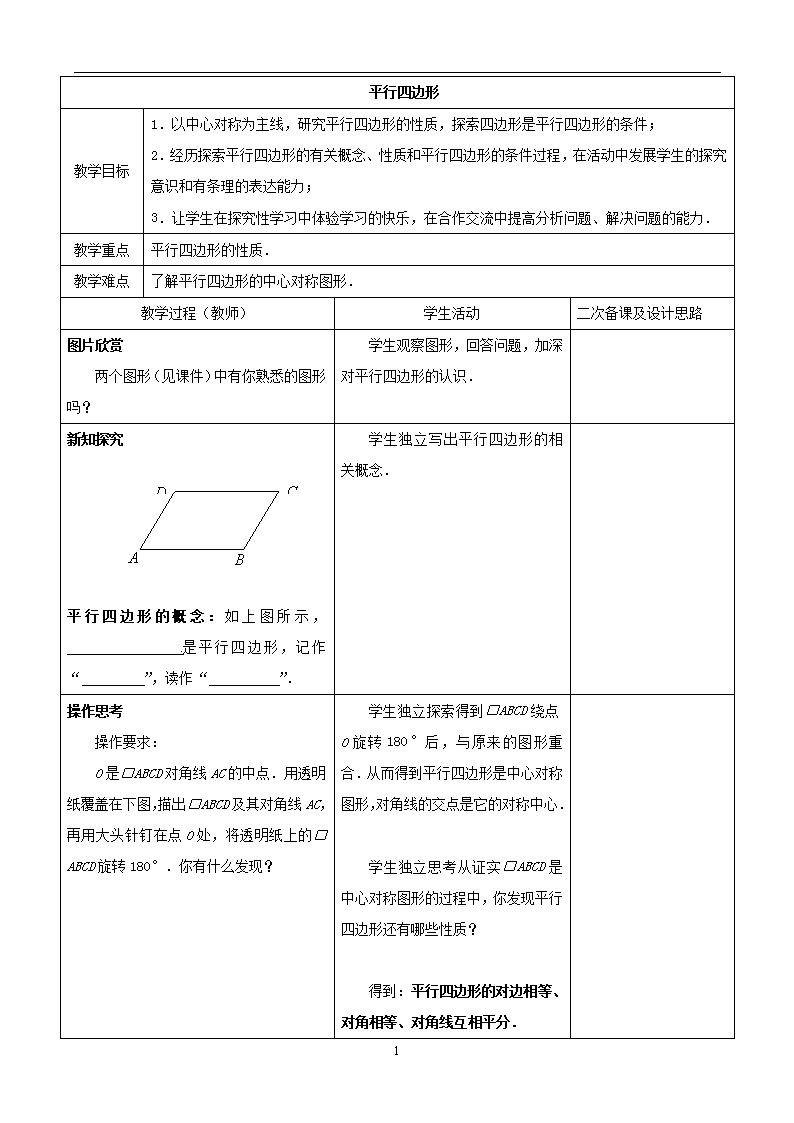
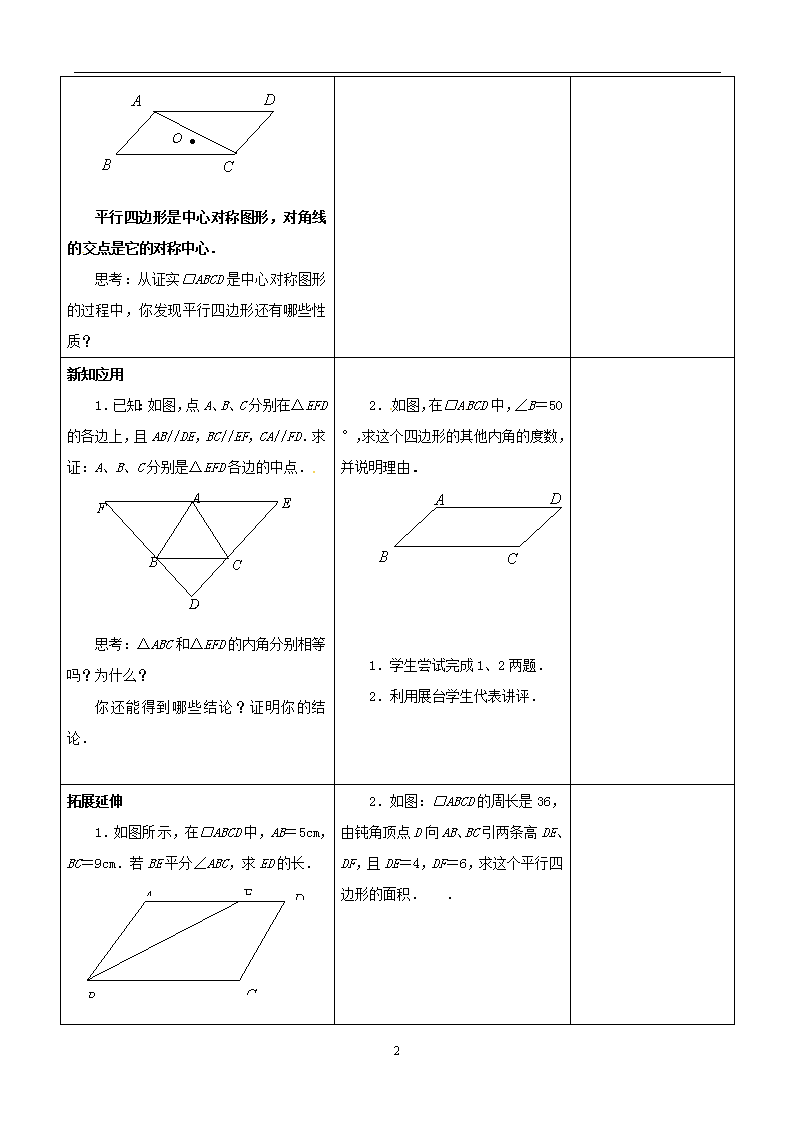
‎ 平行四边形 教学目标 ‎1．以中心对称为主线，研究平行四边形的性质，探索四边形是平行四边形的条件；‎ ‎2．经历探索平行四边形的有关概念、性质和平行四边形的条件过程，在活动中发展学生的探究意识和有条理的表达能力；‎ ‎3．让学生在探究性学习中体验学习的快乐，在合作交流中提高分析问题、解决问题的能力．‎ 教学重点 平行四边形的性质．‎ 教学难点 了解平行四边形的中心对称图形．‎ 教学过程（教师）‎ 学生活动 二次备课及设计思路 图片欣赏 两个图形（见课件）中有你熟悉的图形吗？‎ 学生观察图形，回答问题，加深对平行四边形的认识．‎ 新知探究 A D C B 平行四边形的概念：如上图所示， 是平行四边形，记作“ ”，读作“ ”．‎ 学生独立写出平行四边形的相关概念．‎ 操作思考 操作要求：‎ O是□ABCD对角线AC的中点．用透明纸覆盖在下图，描出□ABCD及其对角线AC，再用大头针钉在点O处，将透明纸上的□ABCD旋转180°．你有什么发现？‎ 学生独立探索得到□ABCD绕点O旋转180°后，与原来的图形重合．从而得到平行四边形是中心对称图形，对角线的交点是它的对称中心．‎ 学生独立思考从证实□ABCD是中心对称图形的过程中，你发现平行四边形还有哪些性质？‎ 得到：平行四边形的对边相等、对角相等、对角线互相平分．‎ 4‎ B A D C O .‎ 平行四边形是中心对称图形，对角线的交点是它的对称中心．‎ 思考：从证实□ABCD是中心对称图形的过程中，你发现平行四边形还有哪些性质？‎ 新知应用 ‎1．已知：如图，点A、B、C分别在△EFD的各边上，且AB//DE ，BC//EF，CA//FD．求证：A、B、C分别是△EFD各边的中点．‎ A B C D E F 思考：△ABC和△EFD的内角分别相等吗？为什么？‎ 你还能得到哪些结论？证明你的结论．‎ ‎2．如图，在□ABCD中，∠B＝50°，求这个四边形的其他内角的度数，并说明理由．‎ B A D C ‎1．学生尝试完成1、2两题．‎ ‎2．利用展台学生代表讲评．‎ 拓展延伸 ‎1．如图所示，在□ABCD中，AB＝5cm，BC＝9cm．若BE平分∠ABC，求ED的长．‎ A B D C E ‎2．如图：□ABCD的周长是36，由钝角顶点D向AB、BC引两条高DE、DF，且DE＝4，DF＝6，求这个平行四边形的面积． ．‎ 4‎ E C B F A D ‎1．学生按照要求独立完成第一题．‎ ‎2．小组交流第二题 ‎ 课堂小结 基础知识：‎ 从观察图形着手，类比归纳出平行四边形的有关概念和平行四边形的性质．‎ 基本思想方法：‎ 用运动变化的观点让学生通过旋转的变换的过程，了解用图形变换识别平行四边行是中心对称图形的方法． ‎ 学生讨论小结本节课内容．‎ 当堂检测：‎ ‎1、已知：□ ABCD中，∠A=100°，你能求出其他各角的度数吗？说说你的理由。‎ ‎2、在 □ABCD中,若BE平分∠ABC，交AD于点E，AB=6，BC=8，则ED＝ ．‎ ‎3、如图，在□ABCD中，两邻边AB、BC的长度之比是1：2，M点是大边AD的中点，则∠BMC= 。‎ ‎4、从平行四边形的一个锐角的顶点做两条高，如果这两条高线的夹角是135°，求这个平行四边形的锐角的度数。‎ ‎5、如图：在□ABCD中，AB=10，BD=8，AC=14，△AOB的周长是多少？为什么？ △ABC与△DBC的周长哪个长？‎ ‎6、平行四边形的两条对角线长分别为8 cm和10 cm，则其边长的范围是 。‎ 4‎ 课后检测：‎ ‎1、为了研究平行四边形的特征，王明、李飞等几个同学对一个平行四边形进行了测量，其结果是：‎ ‎ ①∠A=50°，∠B=50°，∠C=130°，∠D=130°； ②AB=5，BC=10，CD=5，AD=9；‎ ‎ ③∠A=52°，∠B=128°，∠C=50°； ④AB=CD=5，BC=AD=10．‎ ‎ 其中不可能发生的是_____________。‎ ‎2、如图，在□ABCD中，∠ACB=∠B=50°，则∠ACD=_________。‎ ‎3、若平行四边形一内角的平分线把一边分成2 cm和3 cm两部分，则该四边形周长可以是_______cm或_______cm。‎ ‎4、如图在□ABCD中，下列各式不一定正确的是------------ ( ) ‎ ‎ A．∠1+∠2=180° B．∠2+∠3=180°‎ ‎ C．∠ 3+∠4=180° D. ∠2+∠4=180°‎ ‎5、在□ABCD中，∠A比∠B大20°，则∠C的度数为 --------------------------------------------- ( ) ‎ A．60° B．80° C．100° D．120°‎ ‎6、在□ABCD中，对角线AC⊥BD，且AC=8 cm，BD=6 cm，求此平行四边形的面积。‎ ‎7、如图，四边形ABCD是平行四边形，BD⊥AD，AD=12，AB=13，求BC、CD及OB的长。‎ 教后反思：‎ 4‎