8年级数学教案第2讲：正反比例函数综合

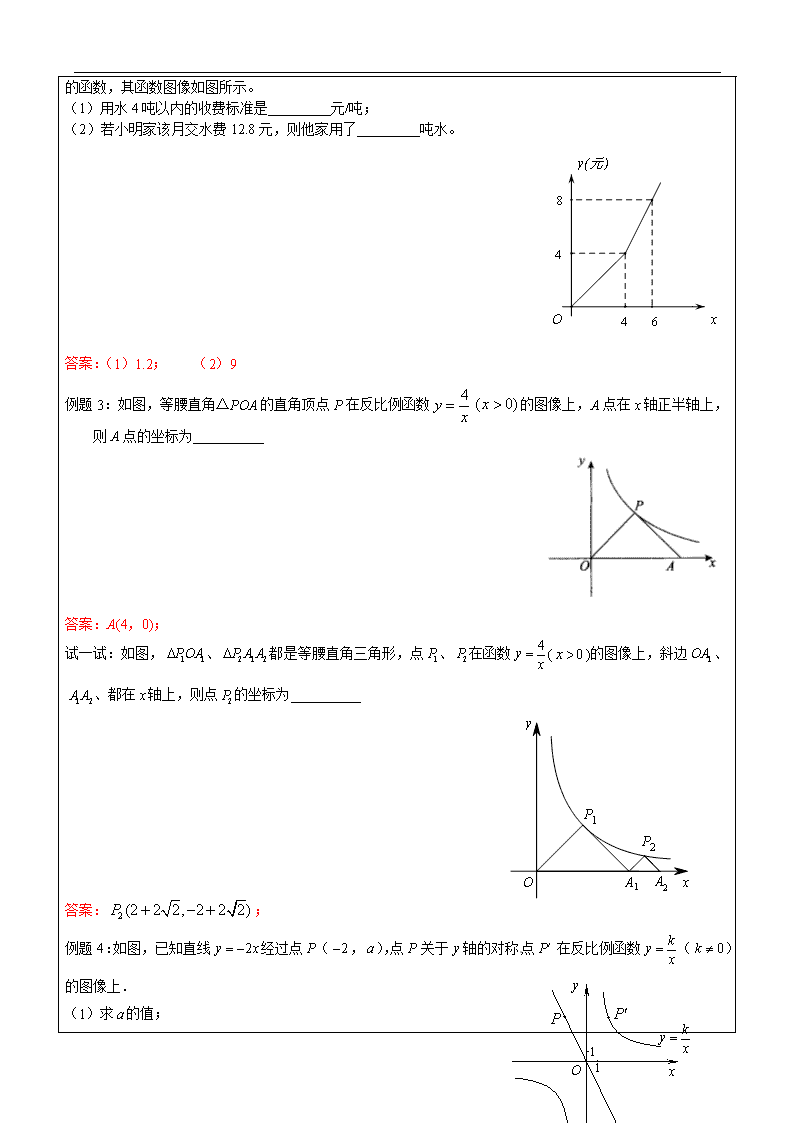
8年级数学教案第2讲：正反比例函数综合

辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 时 间 A / B / C / D / E / F段 主 题 正反比例函数综合 教学内容 ‎1．巩固正反比例函数图像的性质和基本几何图形的性质； ‎ ‎2．培养灵活运用正反比例函数与几何图形的性质解决相关的综合性问题．‎ ‎（此环节设计时间在10-15分钟）‎ 教法说明：要求学生独立完成问题1，再根据问题1的解题思路相互讨论归纳和总结问题2规律．‎ 问题1：反比例函数经过点A（1，4），过点A向x轴、y轴作垂线，垂足为M、N，则矩形AMON的面积为 ，三角形AOM的面积为 ，三角形AON的面积为 ．‎ 问题2：反比例函数经过点A（a，b），过点A向x轴、y轴作垂线，垂足为M、N，则矩形AMON的面积为 ，三角形AOM的面积为 ，三角形AON的面积为 ．‎ 答案：问题1：4，2，2 问题2：‎ 根据以上规律，完成以下两题：‎ ‎1．如图，P是反比例函数图像上第二象限内的一点，且矩形PEOF的面积为3，则反比例函数的解析式是______．‎ ‎2．反比例函数的图像如图所示，点M是该函数图像上一点，MN垂直于x轴，垂足是点N，如果S△MON＝2，则k的值为 ．‎ ‎ ‎ 第1题图 第2题图 答案：1．； 2． ﹣4‎ ‎（此环节设计时间在50-60分钟）‎ 教法指导：重点对例题进行详细讲解，讲解过程中通过提问的形式让学生加深对函数的理解，试一试可以设置为学生间PK，加强生生之间的互动．‎ 例题1：已知函数，与x成反比例，与成正比例，当时，，当时，．　（1）求y关于x的函数的解析式； 　（2）求当时的函数值．‎ 答案：（1），（2）－21‎ 试一试：已知，其中与成正比例，与成反比例，并且当时，当时，求与之间的函数关系式．‎ 答案：‎ 例题2：一个有进、出水管的容器，单位时间内进、出水量都是一定的，设从某时刻开始4分钟内只进水不出水，之后的4分钟内只出水不进水，得到的时间x （分钟）与水量y (升)之间关系如图，求：‎ ‎（1）每分钟进多少升水；‎ ‎（2）每分钟出多少升水；‎ ‎（3）0≤≤4时，y关于x的解析式．‎ 答案：（1）5； （2）1； （3）y＝5x 试一试：我国有很多城市水资源缺乏，为了加强居民的节水意识，某城市制定了每月用水4吨以内（包括4‎ 吨）和用水4吨以上两种收费标准（收费标准：指每吨水的价格），用户每月应交水费y（元）是用水量x(吨)‎ 的函数，其函数图像如图所示。‎ ‎（1）用水4吨以内的收费标准是_________元/吨； ‎ ‎（2）若小明家该月交水费12.8元，则他家用了_________吨水。‎ 答案：（1）1.2； （2）9‎ 例题3：如图，等腰直角△POA的直角顶点P在反比例函数的图像上，A点在x轴正半轴上，则A点的坐标为 ‎ ‎ ‎ 答案：A(4，0)；‎ 试一试：如图，、都是等腰直角三角形，点、在函数()的图像上，斜边、、都在轴上，则点的坐标为 ‎ 答案：；‎ 例题4： x y O P 如图，已知直线经过点P（，），点P关于轴的对称点P′ 在反比例函数（）的图像上．‎ ‎（1）求的值；‎ ‎（2）直接写出点P′ 的坐标；‎ ‎（3）求反比例函数的解析式．‎ 答案：（1）4， （2）（2，4）， （3）‎ 试一试：如图，点P是一个反比例函数与正比例函数的图象的交点，PQ垂直于x轴，垂足Q的坐标为(2，0)．‎ ‎(1) 求这个反比例函数的解析式．‎ ‎(2) 如果点M在这个反比例函数的图象上,且△MPQ的面积为6，求点M的坐标．‎ 答案：O Q x P y （1）； （2）‎ 此环节设计时间在30分钟左右（20分钟练习+10分钟互动讲解）。‎ ‎1．已知，与成正比例，与成正比例；并且当时，；当时，求与的函数关系式.‎ 答案：设，，则，则 ‎ 解得 ‎ 所以 ‎75‎ ‎50‎ ‎25‎ O ‎50‎ ‎75‎ ‎100‎ x(千瓦时)‎ ‎25‎ ‎70‎ ‎100‎ y(元)‎ ‎2．为缓解用电紧张的矛盾，某电力公司特制定了新的用电收费标准，每月用电量（单位：千瓦时）与应付电费（单位：元)的关系如图所示.‎ ‎（1）根据图像，请求出当时，与的函数关系式.‎ ‎（2）请回答：①若每月用电量不超过50千瓦时，收费标准是多少? ‎ ‎ ②若每月用电量超过50千瓦时，收费标准是多少? ‎ 答案：，0.5元/千瓦时，0.9元/千瓦时 ‎3．如图，反比例函数的图像上有两点C、D，其中点D的坐标为，点C的横坐标为4．‎ ‎（1）试确定反比例函数的关系式；‎ ‎（2）的面积与梯形ABCD的面积有什么数量关系？并求出的面积。‎ 答案：（1）（2），‎ 补充类试题：‎ ‎1．两个反比例函数和在第一象限内的图像如图所示，动点P在的图像上，轴于点C，交的图像于点A，轴于点D，交的图像于点B．‎ ‎（1）四边形PAOB的面积是否为定值？说明理由．‎ ‎（2）若点P的坐标为，的面积分别记为、，设．求的值；并用表示S．‎ 答案：（1）四边形PAOB的面积为定值；理由如下：‎ 设△AOC与△BOD的面积分别为S1，S2，矩形PCOD的面积为S3，‎ 可知：S1＝S2＝k2，S3=k1，‎ ‎∴S四边形PAOB=S3-（S1+S2）=k1-k2，‎ ‎∴四边形PAOB的面积是定值；‎ ‎（2）解：由题意知：k1=xPyP=10；‎ A、B两点坐标分别为:，‎ S△ABP＝‎ ‎∴S＝S四边形PAOB−2S△ABP＝10−k2−2×‎ ‎（此环节设计时间在5-10分钟内）‎ 让学生回顾本节课所学的重点知识，以学生自我总结为主，学科教师引导为辅，为本次课做一个总结回顾 函数的解析式求法：‎ 函数中三角形面积的求法：‎ ‎1．已知与成正比例，且 ‎（1）求出与之间的函数关系式； （2）点A在这个函数图像上，求的值 答案：（1）； （2）‎ ‎2．已知正比例函数与反比例函数的图象的一个交点的横坐标是1，求反比例函数的解析式 答案：‎ ‎3．为了预防“流感”，某学校对教室采用“药熏”消毒法进行消毒．已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧完后，y与x成反比例（如图所示）．现测得药物4分钟燃毕，此时室内空气中每立方米含药量为8毫克．请根据题中所提供的信息，解答下列问题：‎ ‎（1）求药物燃烧时，y关于x的函数解析式及定义域；‎ ‎（2）求药物燃烧完后，y关于x的函数解析式及定义域；‎ ‎（3）研究表明，当空气中每立方米的含药量不低于2毫克时，才能有效地杀灭空气中的病菌，那么此次消毒有效时间有多长？‎ 答案：解：（1）∵正比例函数的图像经过点P（4，8），‎ ‎∴正比例函数的解析式为．‎ 定义域为0≤x≤4．‎ ‎（2）∵反比例函数的图像经过点P（4，8），‎ ‎∴反比例函数的解析式为．‎ 定义域为x≥4．‎ ‎（3）把代入中得，‎ 把代入中得6，‎ ‎16-1=15，∴此次消毒的有效时间为15分钟．‎ 预习思考：几何证明中常用倍长中线法来证明，请认真阅读以下内容并完成相关习题。‎ 倍长中线法：延长中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。倍长中线法多用于构造全等三角形和证明边之间的关系。‎ 数学语句描述：如图，在△ABC中，AD是BC边中线；在利用倍长中线法解题时，用准确的语句描述下图所添加的辅助线：延长AD到E使AD=DE，联结BE，可证明△ACD≌△EBD 。‎ ‎1．在△ABC中，AC=5，中线AD=7，则AB边的取值范围是( ) A.2＜AB＜12 B.4＜AB＜12 C.9＜AB＜19 D.10＜AB＜19 ‎ 答案：C ‎2.如图，点E是BC的中点，∠BAE=∠CDE，延长DE到点F使得EF=DE，联结BF，则下列说法正确的是（ ）‎ ‎①BF∥CD ②△BFE≌△CDE ③AB=BF ④△ABE为等腰三角形 A.①②③ B.②③④ C.①③④ D.①②③④ ‎ 答案：A