苏教版八年级数学上册期中考试检测试卷

苏教版八年级数学上册期中考试检测试卷

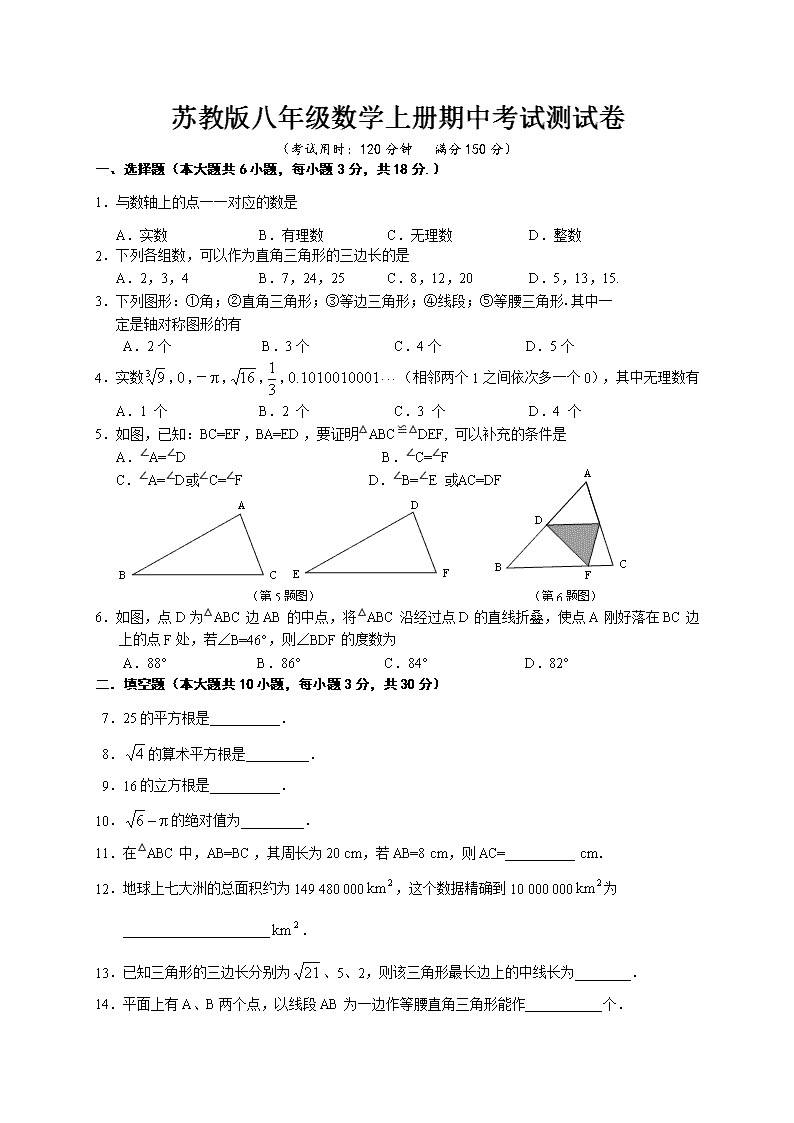
（第 5题图） （第 6题图） 苏教版八年级数学上册期中考试测试卷 （考试用时：120 分钟 满分 150 分） 一、选择题（本大题共 6 小题，每小题 3 分，共 18 分.） 1．与数轴上的点一一对应的数是 A．实数 B．有理数 C．无理数 D．整数 2．下列各组数，可以作为直角三角形的三边长的是 A．2，3，4 B．7，24，25 C．8，12，20 D．5，13，15. 3．下列图形：①角；②直角三角形；③等边三角形；④线段；⑤等腰三角形.其中一 定是轴对称图形的有 A．2个 B．3个 C．4个 D．5个 4．实数  1010010001.0 3 116093 ，，，－，， （相邻两个 1之间依次多一个 0），其中无理数有 A．1 个 B．2 个 C．3 个 D．4 个 5．如图，已知：BC=EF，BA=ED，要证明△ABC≌△DEF, 可以补充的条件是 A．∠A=∠D B．∠C=∠F C．∠A=∠D或∠C=∠F D．∠B=∠E 或AC=DF 6．如图，点 D为△ABC边 AB的中点，将△ABC沿经过点 D的直线折叠，使点 A刚好落在 BC边 上的点 F处，若∠B=46°，则∠BDF的度数为 A．88° B．86° C．84° D．82° 二．填空题（本大题共 10 小题，每小题 3 分，共 30 分） 7．25的平方根是__________． 8． 4 的算术平方根是_________． 9．16的立方根是__________． 10． 6 的绝对值为_________． 11．在△ABC中，AB=BC，其周长为 20 cm，若 AB=8 cm，则 AC=__________ cm． 12．地球上七大洲的总面积约为 149 480 000 2km ，这个数据精确到 10 000 000 2km 为 _____________________ 2km ． 13．已知三角形的三边长分别为 21、5、2，则该三角形最长边上的中线长为________． 14．平面上有 A、B两个点，以线段 AB为一边作等腰直角三角形能作___________个． （第 15题图） （第 16题图） 15．已知△ABC 为等边三角形，BD 为中线，延长 BC 至 E，使 CE=CD=1，连接 DE，则 DE= ． 16．把一副三角板如图甲放置，其中  90DECACB ，  45A ，  30D ，斜边 12AB  ， 14CD  ，把三角板DCE绕着点C顺时针旋转 15 得到△ 11CED （如图乙），此 时AB与 1CD 交于点O，则线段 1AD 的长度为 ． 三．解答题（本大题共 9 小题，共 102 分） 17．（本题 10分）求下列各式中的 x： (1) 25 2 8x   ； (2) 64)1( 3 x ． 18．（本题 10分）求下列各式的值： (1) 16 918)4( 32  ； (2)   322 27103   ． 19．（本题 10分） 下图是单位长度为 1的正方形网格． （1）在图 1中画出一条长度为 10 的线段 AB； （2）在图 2中画出一个以格点为顶点，面积为 5的正方形． 图 1 图 2 20．（本题 10分） 已知四边形 ABCD中，∠A为直角，AB＝16，BC＝25，CD＝15，AD＝12，求四边形 ABCD 的面积． 21．（本题 12分） 作图题（不写作法，保留作图痕迹）： （1）如图，四边形 ABCD是长方形，用直尺和圆规作出∠A的平分线与 BC边的垂直平分线的 交点 Q． （2）用直尺和圆规在如图所示的数轴上作出 13 的点 A． 22．（本题 12分） 如图，在△ABC中，D是BC边上的点（不与B，C重合），F，E分别是AD及其延长线上的点， CF∥BE． 请你添加一个条件，使△BDE≌△CDF（不再添加其它线段，不再标注或使用其他 字母），并给出证明． （1）你添加的条件是： ； （2）证明： [中#国~教育@*出%版网] 23．（本题 12分） 如图，数轴上有一个等边△AOC，点 O与原点重合，点 A与表示－5的点重合，△AOC经过平 移或轴对称或旋转都可以得到△OBD． （1）△AOC沿数轴向右平移得到△OBD，则平移的距离是__________个单位长度； △AOC与△BOD关于直线对称，则对称轴是______________________________； △AOC绕原点 O顺时针．．．旋转得到△DOB，则旋转角度至少是__________度； （2）连结 AD，交 OC于点 E，求∠AEO的度数． 24．（本题 12分） 如图，已知：在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点 C，D，E三点 在同一条直线上，连接 BD．图中的 CE、BD有怎样的大小和位置关系？试证明你的结论． 25．（本题 14分） 如图，在△ABC中，AB=BC，CD⊥AB于点 D， CD＝BD，BE 平分∠ABC，点 H是 BC边的 中点，连接 DH，交 BE于点 G，连接 CG [来． (1)求证：△ADC≌△FDB； (2)求证：CE＝ 2 1 BF； (3)判断△ECG的形状，并证明你的结论； (4)猜想 BG与 CE的数量关系，并证明你的结论．