八年级下数学课件《三角形的中位线》 (4)_苏科版

八年级下数学课件《三角形的中位线》 (4)_苏科版

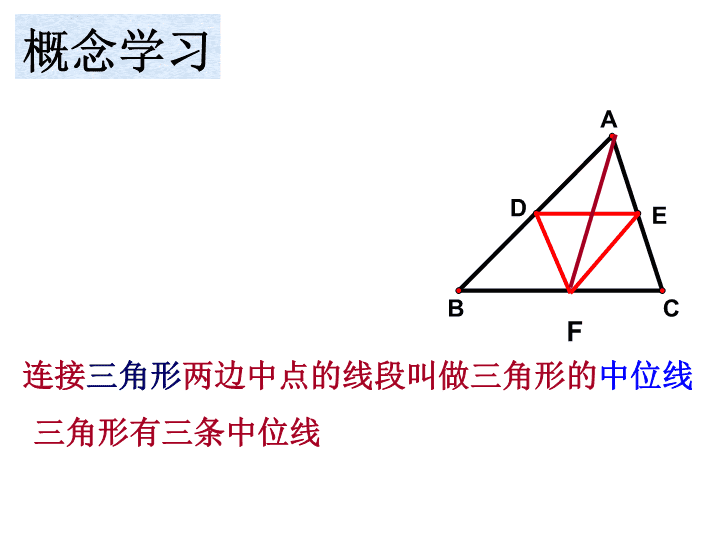
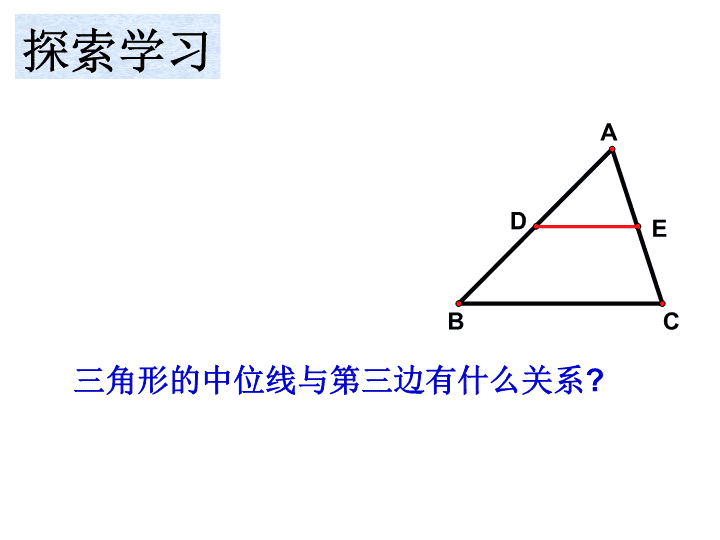
A B C D E 概念学习 连接三角形两边中点的线段叫做三角形的中位线 F 三角形有三条中位线 A B C D E 探索学习 三角形的中位线与第三边有什么关系? C ED F B A 返回 证明：如图，以点E为旋转中心，把 ⊿ADE绕点E，按顺时针方向旋转180゜， 得到⊿CFE，则D，E，F同在一直线上 DE=EF，且⊿ADE≌⊿CFE。 ∴∠ADE=∠F，AD=CF， ∴AB∥CF。 又∵BD=AD=CF， ∴四边形BCFD是平行四边形（一组对边平 行且相等的四边形是平行四边形）， ∴DF∥BC（根据什么？）， ∴DE 1/2BC C ED F B A 证法二：过点C作AB的平行 线交DE的延长线于F ∵CF∥AB， ∴∠A=∠ECF 又AE=EC，∠AED=∠CEF ∴△ADE≌ △CFE ∴ AD=FC 又DB=AD， ∴DB FC ∴四边形BCFD是平行四边形 ∴DE// BC 且DE=EF=1/2BC 返回 A B C ED F 证法三：如图，延长DE至F, 使EF=DE， 连接CD、AF、CF ∵AE=EC ∴DE=EF ∴四边形ADCF是平行四边形 ∴AD FC 又D为AB中点， ∴DB FC ∴四边形BCFD是平行四边形 ∴DE// BC 且DE=EF=1/2BC返回 A C ED F G B 证法四：如图，过E作AB的平行线交 BC于F，自A作BC的平行线交FE于G ∵AG∥BC∴∠EAG=∠ECF 又∵ AE=EC, ∠AEG=∠CEF ∴△AEG≌ △CEF∴AG=FC，GE=EF 又AB∥GF，AG∥BF∴四边形ABFG 是平行四边形 ∴BF=AG=FC，AB=GF 又D为AB中点，E为GF中点， ∴DB EF ∴四边形DBFE是平行四边形 ∴DE∥BF，即DE∥BC，DE=BF=FC 即DE=1/2BC 返回 　　三角形的中位线平行于第三边， 并且等于第三边的一半. 已知：如图，D、E分别是 △ABC的边AB、AC的中点. 求证：DE∥BC， BCDE 2 1 C ED B A 三角形的中位线平行且等于第三边的一半. 几何语言： ∵DE是△ABC的中位线 （或AD=BD,AE=CE) C ED B A BC2 1//DE∴ ① 证明平行问题 ② 证明一条线段是另一条线段的两倍或一半 用 途 B D A E CF 三条中位线围 成一个新的三角形， 它与原来的三角形 有无关系?哪方面 有关系? (1) △DEF的周长与 △ABC的周长有什么关系? (2) △DEF的面积与 △ABC的面积有什么关系? 一个三角形有几条中位线呢？ 三角形有三条中位线 因为 D、 E分别为AB、 AC 的中点 所以 DE为 △ ABC的中位线 三角形的中位线和三角形的中线不同注意 同理DF、 EF也为 △ ABC的中位线 ED F A CB 三角形面积为20平方厘米，则 它的三条中位线围成的三角形 面积是 已知：在四边形ABCD中， E，F分别是对角线AC，BD 的中点，M，N分别是AB， CD的中点。求证：EF与 MN互相平分（5分） 一个三角形中位线有几条？ 顺次连结平行四边形各边中点 所得的四边形是什么图形？ 三角形周长为10厘米，则它的 三条中位线围成的三角形周长 是？ 在四边形ABCD中，AB=CD， M，N，P分别AD，BC，BD的 中点。求证：∠PNM=∠PMN （4分） 在ΔABC中，D，E分别是AB、 CD边上的中点。M、N分别是 DB、BE边上的中点。AC=6， 则MN= DE是RtΔABC的中位线，AF是 斜边BC上的中线，则DE与AF 有何数量关系？（3分） A B C D E F G H 小明说任意画一个四边形，连接各边的中点， 所得的四边形一定就是平行四边形。 你认为他 说的对吗？ 已知：如图，在四边形ABCD中，E、F、G、H分别是 AB、BC、CD、DA的中点. 求证：四边形EFGH是平行四边形. A B C D E F G H 证明：如图，连接AC ∵EF是△ABC的中位线 AC2 1//EF 同理得： AC2 1//GH EF//GH ∴四边形EFGH是平行四边形 ①有中点连线而无三角形,要作辅助线产生三角形 ②有三角形而无中位线,要连结两边中点得中位线 222111 333 小结小结小结 方法点拨： 在处理问题时,要求同时出现三角形及中位线 ①有中点连线而无三角形,要作辅助线产生三角形 ②有三角形而无中位线,要连结两边中点得中位线 定 理 应 用： ⑴定理为证明平行关系提供了新的工具 ⑵定理为证明一条线段是另一条线段的2倍或 1/2提 供了一个新的途径 222111 333 提高提高提高 1.已知: 如图,DE,EF是⊿ABC的两条中位 线.求证:四边形BFED是平行四边形. D B CF E A 222111 333 小结小结小结 222 333 小结小结小结 222111 小结小结小结