2020八年级数学下册 第一章 三角形的证明 等腰与直角三角形导学案（无答案）（新版）北师大版

2020八年级数学下册 第一章 三角形的证明 等腰与直角三角形导学案（无答案）（新版）北师大版

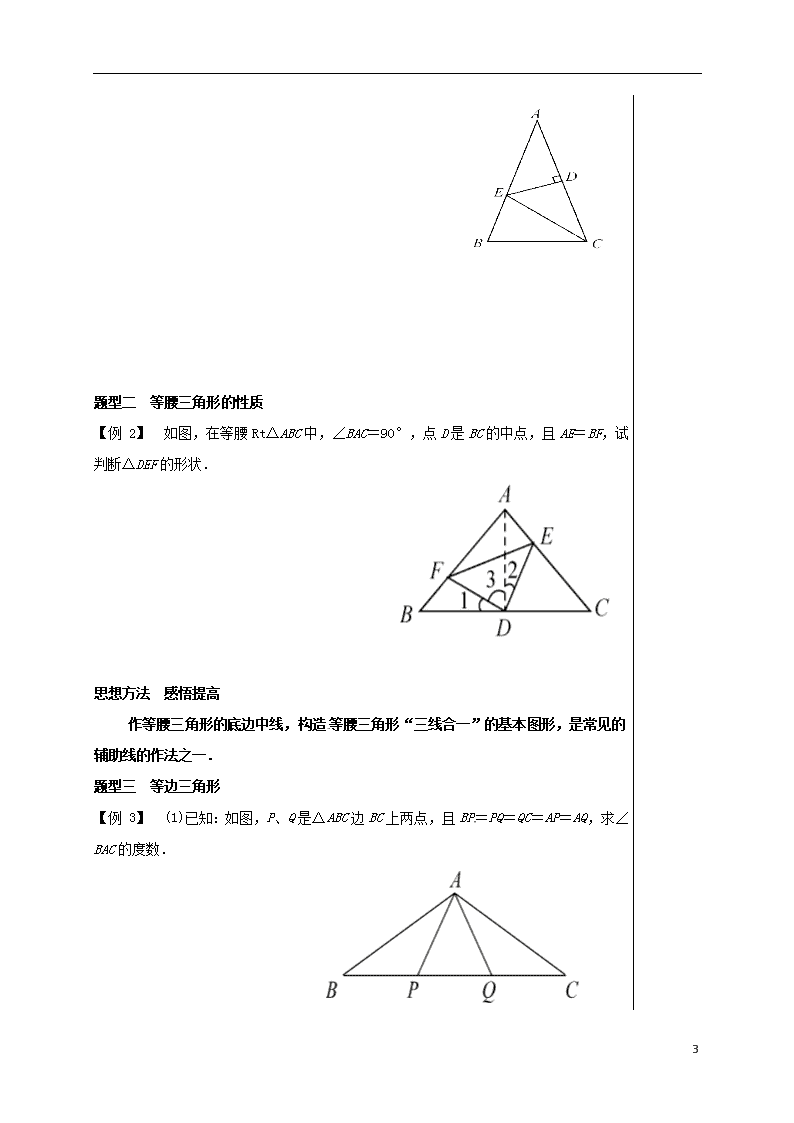
课题：等腰与直角三角形 班级: 姓名: 小组: 评价: ‎ ‎【学习目标】‎ ‎(1)掌握等腰、等边、直角三角形的定义、性质与判定。‎ ‎(2)运用特殊三角形的性质与判定解决几何问题。‎ ‎【重点难点】‎ ‎(1)掌握等腰、等边、直角三角形的定义、性质与判定。‎ ‎(2)运用特殊三角形的性质与判定解决几何问题。‎ ‎【导学流程】‎ 一、基础感知 ‎1．等腰三角形：‎ ‎ (1)性质： 相等， 相等，________________________叫“三线合一”；‎ ‎ (2)判定：有两边相等、两角相等的三角形是等腰三角形．‎ ‎2．等边三角形：‎ ‎ (1)性质： 相等，三内角都等于 ；‎ ‎ (2)判定：三边相等、三内角相等或__________________等腰三角形是等边三角形．‎ ‎3．直角三角形：在△ABC中，∠C＝90°.‎ ‎ 性质：(1)边与边的关系：(勾股定理)a2＋b2＝ ；‎ ‎ (2)斜边上的中线等于斜边的_____； ‎ ‎ (3)角与角的关系：∠A＋∠B＝ ；‎ ‎ (4)边与角的关系： 若∠A＝30°，则30°角所对的直角边等于斜边的______.‎ ‎ 判定： ①有一个角是直角的三角形是直角三角形； ‎ ‎ ②如果三角形的三边长a、b、c满足a2＋b2＝c2，那么这个三角形是直角三角形； ‎ 问题记录 4‎ ‎ ④有两个角互余的三角形是直角三角形。‎ ‎ (5)利用HL证明全等 二、深入学习 ‎1．如果一个等腰三角形的两边长分别是‎5 cm和‎6 cm，那么此三角形的周长是(　　)‎ ‎ A．‎15 cm B．‎16 cm C．‎17 cm D．‎16 cm或‎17 cm ‎2. 如图，△ABC中，AB=AC,∠B=70°，则∠A的度数是（ ）‎ A B D C A.70° B. 55° C. 50° D. 40° ‎ A B C ‎3、如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（　　）  A． 30°   B． 36°   C． 40°  D． 45° ‎ ‎4、若直角三角形的两直角边长为a、b，且满足，则该直角三角形的斜边长为　　．‎ ‎5、已知直角三角形两边的长分别是3和4，则第三边的长为_______。 ‎ 三、题型分类 深度剖析 题型一　等腰三角形有关边角的讨论 ‎ ‎【例 1】　方程x2－9x＋18＝0的两个根是等腰三角形的底和腰，则这个三角形的周长为(　　)‎ ‎ A．12 B．12或‎15 ‎ C．15 D．不能确定 ‎2、若等腰三角形的一个角为50°，则它的顶角是（ ）。‎ 知能迁移 ‎(如图， △ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC.‎ ‎①求∠ECD的度数；‎ ‎②若CE＝5，求BC长． ‎ 4‎ 题型二　等腰三角形的性质 ‎【例 2】　如图，在等腰Rt△ABC中，∠BAC＝90°，点D是BC的中点，且AE＝BF，试判断△DEF的形状．‎ 思想方法 感悟提高　 ‎ ‎ 作等腰三角形的底边中线，构造等腰三角形“三线合一”的基本图形，是常见的辅助线的作法之一．‎ 题型三　等边三角形 ‎【例 3】　(1)已知：如图，P、Q是△ABC边BC上两点，且BP＝PQ＝QC＝AP＝AQ，求∠BAC的度数．‎ 4‎ ‎2.如图所示，已知△ABC和△DCE均是等边 三角形，点B、C、E在同一条直线上，AE与BD交于点 O，AE与CD交于点G，AC与BD交于点F，连接OC、FG， 则下列结论：①AE＝BD；②AG＝BF； ③FG∥BE； ④∠BOC＝∠EOC.其中正确结论的个数(　　)‎ A．1个 B．2个 C．3个 D．4个 思想方法 感悟提高 ‎ ‎ 在解题的过程中要充分利用等边三角形特有的性质，每个角都相等，每条边都相等，这可以让我们轻松找到证明全等所需的条件．‎ 题型四　直角三角形、勾股定理 ‎ ‎【例 4】如图‎2-7-1‎，已知AB=CD，DE⊥AC，BF⊥AC，E、F为垂足，DE=BF，问：AB与CD平行吗？说明理由.‎ 三、迁移运用 如图‎2-7-21‎，在△ABC中，AB=AC，∠BAC＝120°，∠ABC的平分线BD交AC于点D，从点D引BA的垂线，垂足是E，如果AE=1，那么CD=_________.‎ 4‎ 4‎