人教版八年级数学上册第十二章复习课件PPT

人教版八年级数学上册第十二章复习课件PPT

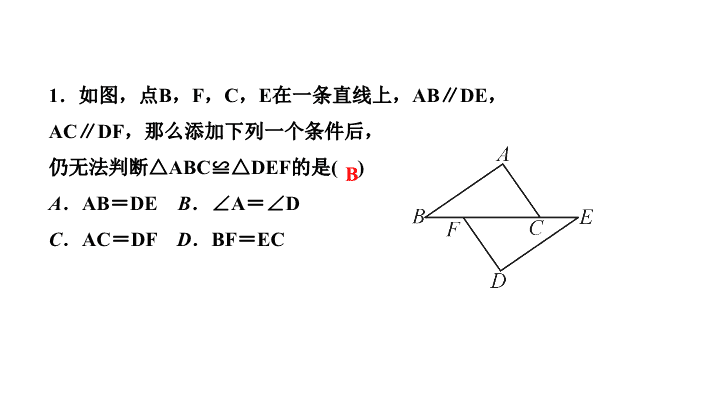
第十二章　全等三角形 人教版 章末复习 (二)　全等三角形 1 ．如图，点 B ， F ， C ， E 在一条直线上， AB ∥ DE ， AC ∥ DF ，那么添加下列一个条件后， 仍无法判断 △ ABC ≌△ DEF 的是 ( ) A ． AB ＝ DE B ． ∠ A ＝ ∠ D C ． AC ＝ DF D ． BF ＝ EC B 2 ．如图，将两根钢条 AA′ ， BB′ 的中点 O 连在一起， 使 AA′ ， BB′ 可以绕着点 O 自由转动，就做成了一个测量工件， 由三角形全等得出 A′B′ 的长等于内槽宽 AB. 那么判定 △ OAB ≌△ OA′B′ 的理由是 ( ) A ． SAS B ． ASA C ． SSS D ． AAS A 3 ． (2019 · 镇江节选 ) 如图，四边形 ABCD 中， AD ∥ BC ，点 E ， F 分别 在 AD ， BC 上， AE ＝ CF ，过点 A ， C 分别作 EF 的垂线，垂足为 G ， H . 求证：△ AGE ≌△ CHF . 4 ．如图，已知 AB ＝ AC ， AD ＝ AE ，∠ BAC ＝∠ DAE . 下列结论不正确的是 ( ) A ．∠ BAD ＝∠ CAE B ．△ ABD ≌△ ACE C ． AB ＝ BC D ． BD ＝ CE 5 ．如图， AB ＝ AC ， CD ⊥ AC 于点 C ， BE ⊥ AB 于点 B ， AE 交 BC 于点 F ，且 BE ＝ CD ，下列结论不一定正确的是 ( ) A ．∠ BAC ＝∠ DAE B ． BF ＝ EF C ． AE ＝ AD D ．∠ BAE ＝∠ CAD C B 6 ．如图，两根旗杆间相距 12 m ，某人从点 B 沿 BA 走向点 A ， 一段时间后他到达点 M ，此时他仰望旗杆的顶点 C 和 D ， 两次视线的夹角为 90° ，且 CM ＝ DM. 已知旗杆 AC 的高为 3 m ， 该人的运动速度为 1 m / s ，则这个人运动到点 M 所用时间是 ____ s . 3 7 ．如图，在△ ABC 和△ ADE 中， AB ＝ AC ， AD ＝ AE ， ∠ BAC ＝∠ DAE ，点 C 在 DE 上．求证： (1)△ ABD ≌△ ACE ； (2)∠ ACD ＝∠ BDA ＋∠ BAD . (2)∵△ ABD ≌△ ACE ，∴∠ BDA ＝∠ AEC ， ∠ BAD ＝∠ CAE .∵∠ ACD ＝∠ AEC ＋∠ CAE ， ∴∠ ACD ＝∠ BDA ＋∠ BAD 8 ．如图是一块三角形的草坪，现要在草坪上建一凉亭供大家休息， 要使凉亭到草坪三条边的距离相等，凉亭的位置应选在 ( ) A ．△ ABC 三条中线的交点处 B ．△ ABC 三条角平分线的交点处 C ．△ ABC 三条高所在直线的交点处 D ．△ ABC 三边的中垂线的交点处 B 9 ．如图， AD 是△ ABC 的角平分线， DF⊥AB ，垂足为 F ， DE ＝ DG ， △ ADG 和△ AED 的面积分别为 50 和 39 ，则△ EDF 的面积为 ( ) A ． 11 B ． 5.5 C ． 7 D ． 3.5 B 10 ．如图，已知 BD ⊥ AN 于点 B ，交 AE 于点 O ， OC ⊥ AM 于点 C ， 且 OB ＝ OC ，如果∠ OAB ＝ 25° ，则∠ ADB ＝ ____ ． 40° 11 ．如图，点 C 在 ∠ AOB 的 OB 边上，用尺规作出了 ∠ AOB ＝ ∠ NCB ， 作图痕迹中，弧 FG 是 ( ) A ．以点 C 为圆心， OD 为半径的弧 B ．以点 C 为圆心， DM 为半径的弧 C ．以点 E 为圆心， OD 为半径的弧 D ．以点 E 为圆心， DM 为半径的弧 D 11 ．已知：如图， CD ⊥ AB 于点 D ， BE ⊥ AC 于点 E ， BE ， CD 相交于点 O . 求证： (1) 当∠ 1 ＝∠ 2 时， OB ＝ OC ； (2) 当 OB ＝ OC 时，∠ 1 ＝∠ 2. 12 ．如图，点 C 在∠ AOB 的边 OB 上，用尺规作出了∠ AOB ＝∠ NCB ， 作图痕迹中，弧 FG 是 ( ) A ．以点 C 为圆心， OD 为半径的弧 B ．以点 C 为圆心， DM 为半径的弧 C ．以点 E 为圆心， OD 为半径的弧 D ．以点 E 为圆心， DM 为半径的弧 D 15 14 ．如图，铁路 OA 和铁路 OB 交于点 O 处，河道 AB 与铁路分别交于点 A 处 和点 B 处，试在河岸上建一座水厂 M ，要求 M 到铁路 OA ， OB 的距离相等， 则该水厂 M 应建在图中什么位置？请在图中标出点 M 的位置． ( 保留作图痕迹，不写作法 ) 解：作∠ AOB 的平分线交 AB 于点 M ，点 M 即为水厂的位置，如图 【 核心素养 】 15 ． 【 动态问题 】 如图①， AB ＝ 4 cm ， AC ⊥ AB ， BD ⊥ AB ， AC ＝ BD ＝ 3 cm. 点 P 在线段 AB 上以 1 cm/s 的速度由点 A 向点 B 运动， 同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 t (s). (1) 若点 Q 的运动速度与点 P 的运动速度相等，当 t ＝ 1 时，△ ACP 与△ BPQ 是否全等，并判断此时线段 PC 和线段 PQ 的位置关系，请分别说明理由； (2) 如图②，将图①中的“ AC ⊥ AB ， BD ⊥ AB ” 改为 “∠ CAB ＝∠ DBA ＝ 60°” ，其他条件不变．设点 Q 的运动速度为 x cm/s ， 是否存在实数 x ，使得△ ACP 与△ BPQ 全等？ 若存在，求出相应的 x ， t 的值；若不存在，请说明理由．