八年级数学下册第2章四边形2-6菱形2-6-1菱形的性质课件（湘教版）

八年级数学下册第2章四边形2-6菱形2-6-1菱形的性质课件（湘教版）

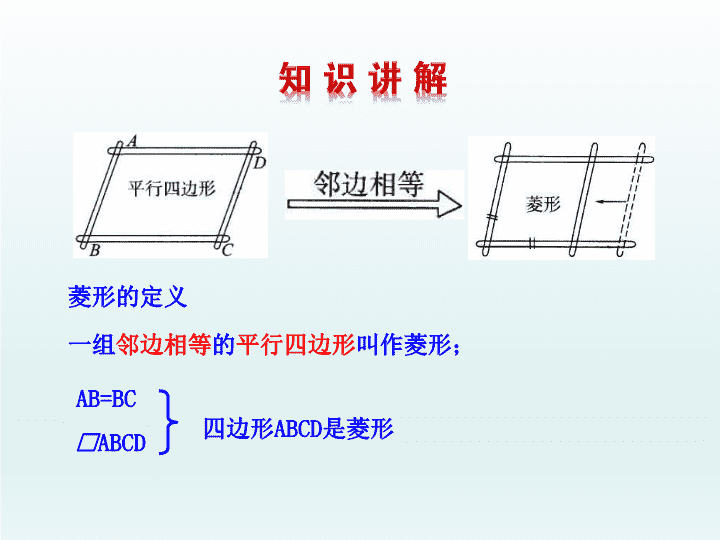
2.6 菱形 2.6.1 菱形的性质 A B C D O 1. 掌握菱形的概念，知道菱形与平行四边形的关系 . 了解菱形既是中心对称图形又是轴对称图形 . 2. 理解并掌握菱形的定义及性质，会用这些性质进行有关的证明和计算，会计算菱形的面积 . 一组 邻边相等 的 平行四边形 叫作菱形； AB=BC 四边形 ABCD 是菱形 □ ABCD 菱形的定义 小明是这样做的：将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可 . 你知道其中的道理吗？ 如何利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片？ 已知四边形 ABCD 是菱形 1. 图中有哪些相等的线段？ 2. 图中有哪些相等的角？ 3. 图中有哪些等腰三角形？ 4. 图中有哪些直角三角形？ 5. 菱形是轴对称图形吗？它有几条对称轴？分别是什么？对称轴间有什么关系？ A B C D O 1 2 3 4 5 6 7 8 已知四边形 ABCD 是菱形 1. 相等的线段： AB=CD=AD=BC ， OA=OC ， OB=OD A B C D O 1 2 3 4 5 6 7 8 ∠DAB=∠BCD ， ∠ ABC =∠CDA ， ∠AOB=∠DOC=∠AOD=∠BOC =90° ， ∠1=∠2=∠3=∠4 ，∠ 5=∠6=∠7=∠8 2. 相等的角： A B C D O 1 2 3 4 5 6 7 8 3. 等腰三角形有： △ABC ，△ DBC ，△ ACD ，△ ABD A B C D O 1 2 3 4 5 6 7 8 4. 直角三角形有： Rt△AOB ， Rt△BOC ， Rt△COD ， Rt△DOA A B C D O 1 2 3 4 5 6 7 8 5. 菱形是轴对称图形，有两条对称轴，为两条对角线所在直线，两条对称轴垂直 . A B C D O 菱形的性质： （ 1 ）菱形的对边相等，对角相等，对角线互相平分； （ 2 ）菱形的四条边都相等； （ 3 ）菱形的对角线互相垂直，并且每一条对角线平分一组对角； （ 4 ）菱形是轴对称图形 , 两条对角线所在的直线都是它的对称轴； （ 5 ）菱形是中心对称图形，对角线的交点是对称中心 . 求证： AC⊥BD ； AC 平分∠ BAD 和∠ BCD ； BD 平分∠ ABC 和∠ ADC. 已知：菱形 ABCD 的对角线 AC 和 BD 相交于点 O. 证明： 因为四边形 ABCD 是菱形， A B C D O 在△ ABD 中，又因为 BO=DO ， 所以 AB=AD （菱形的四条边都相等） 所以 AC⊥BD ， AC 平分∠ BAD ， 命题： 菱形的对角线互相垂直平分，并且每一条对角线平分一组对角 . 同理： AC 平分∠ BCD ； BD 平分 ∠ ABC 和∠ ADC. 上述的命题也是一个定理 . 菱形的两条对角线互相平分 菱形的两组对边平行且相等 边 对角线 角 菱形的四条边相等 菱形的两组对角分别相等 菱形的邻角互补 菱形的两条对角线互相垂直平分，每一条对角线平分一组对角 . A D C B O 菱形的性质 【 菱形的面积公式 】 菱 形 A B C D O E S 菱形 =BC·AE 思考 : 计算菱形的面积除了上式方法外 , 利用对角线能 计算菱形的面积吗 ? =S △ABD +S △BCD = AC×BD S 菱形 ABCD 菱形的面积 = 底 × 高 = 对角线乘积的一半 A B C D O 【 例题 】 【 解析 】 【 跟踪训练 】 【 解析 】 答案： 【 解析 】 答案： 【 证明 】 1. （陕西 · 中考）若一个菱形的边长为 2 ，则这个菱形两条对角线的平方和为（ ） (A)16 (B)8 (C)4 (D)1 【 解析 】 选 A. 设这个菱形两条对角线长分别为 a,b. 由菱形对角线互相垂直且平分，则 即 a 2 +b 2 =16. 【 解析 】 【 解析 】 4. 如图，菱形 ABCD 中，∠ B=60°,AB=2,E 、 F 分别是 BC 、 CD 的中点，连接 AE 、 EF 、 AF ，则△ AEF 的周长为 ( ) （ A ） （ B ） （ C ） （ D ） 3 【 解析 】 选 B. 连接 AC. 因为四边形 ABCD 是菱形，所以 AB ＝ BC. 又因为∠ B ＝ 60° ，所以△ ABC 是等边三角形 . 因为 E 是 BC 的中 点，所以 AE⊥BC. 同理， AF⊥CD. 易证得△ ABE≌△ADF ，所以 AE=AF. 因为 AB∥CD ，∠ B=60°, 所以∠ C=120°. 又因为 CE=CF, 所以∠ CEF ＝ 30° ，所以∠ AEF ＝ 60° ，所以△ AEF 是等边三角 形 . 由勾股定理得 所以△ AEF 的周长为 5. （嘉兴 · 中考）如图，已知菱 形 ABCD 的一个内角∠ BAD=80°, 对角 线 AC 、 BD 相交于点 O ，点 E 在 AB 上，且 BE=BO ，则∠ AOE=____. 【 解析 】 在菱形 ABCD 中， AC⊥BD ， ∠ BAC= ∠BAD=40° ， 得∠ ABD=50° ，由 BE=BO ， 得∠ BOE=∠BEO=65° 所以∠ AOE=25° 答案 : 25° 6. （珠海 · 中考）如图， P 是菱形 ABCD 对角线 BD 上一点， PE⊥AB 于点 E ， PE=4 cm ，则点 P 到 BC 的距离是 ____cm. 【 解析 】 菱形对角线平分一组对角，且角平分线上的点到角两边的距离相等，故点 P 到 BC 的距离是 4 cm. 答案： 4 7. （常德 · 中考）如图，已知四边形 ABCD 是菱形， DE⊥AB,DF⊥BC ，求证：△ ADE≌△CDF. 【 证明 】 在△ ADE 和△ CDF 中，因为四边形 ABCD 是菱形， 所以∠ A=∠C,AD=CD. 又 DE⊥AB,DF⊥BC, 所以∠ AED=∠CFD=90°. 所以△ ADE≌△CDF. 【 解析 】 9. （郴州 · 中考）一种千斤顶利用了四边形的不稳定 性 . 如图，其基本形状是一个菱形，中间通过螺杆连接， 转动手柄可改变∠ ADC 的大小（菱形的边长不变），从而 改变千斤顶的高度（即 A 、 C 之间的距离） . 若 AB=40 cm, 当∠ ADC 从 60° 变为 120° 时，千斤顶升高了多少？ （ ≈ 1.414, ≈1.732 ，结果保留整数） 【 解析 】 连结 AC ，与 BD 相交于点 O ， 因为四边形 ABCD 是菱形 , 所以 AC⊥BD ，∠ ADB=∠CDB ， AC=2AO. 当∠ ADC=60° 时，△ ADC 是等边三角形 . 所以 AC=AD=AB=40. 当∠ ADC=120° 时， ∠ ADO=60° ，∠ OAD=30°, 又 AD=40, 所以 OD=20. 通过本课时的学习，需要我们 1. 掌握 菱形的定义、性质 . 2. 会利用菱形的对角线求菱形的面积 . 3. 会应用菱形的知识解决有关计算和证明的问题 . 少而好学，如日出之阳；壮而好学，如日中之光；老而好学，如炳烛之明。 —— 刘向