- 2021-11-01 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
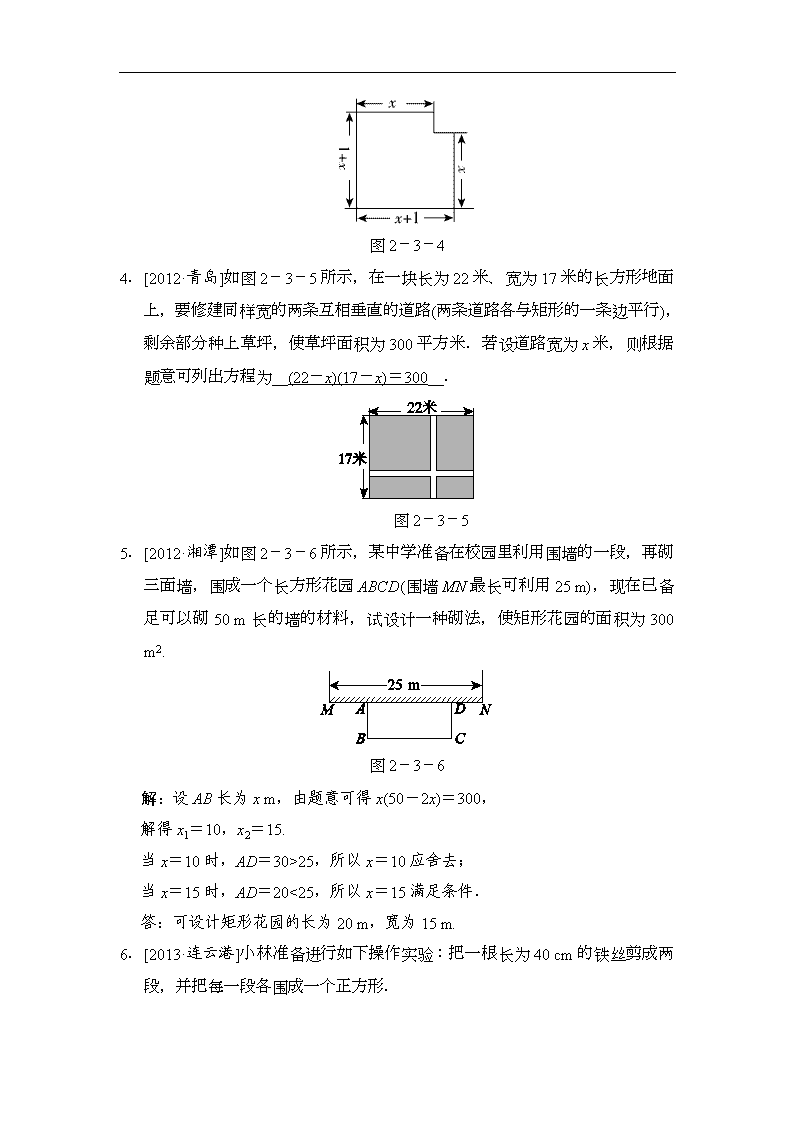
浙教版数学八年级下册《一元二次方程的应用》(第2课时)同步练习
第 2 课时 面积问题[学生用书 B16] 1.在一幅长 80 cm,宽 50 cm 的长方形风景画的四周镶上一条金色纸边,制成 一幅矩形挂图,如图 2-3-2 所示,如果要使整个挂图的面积是 5 400 cm2, 设金色纸边的宽为 x cm,那么 x 满足的方程是 ( D ) 图 2-3-2 A.x2+130x-1 400=0 B.x2-65x-350=0 C.x2-130x-1 400=0 D.x 2+65x-350=0 【解析】 依题意,得(80+2x)(50+2x)=5 400,整理,得 x2+65x-350=0, 故选 D. 2.如图 2-3-3 所示,长方形 ABCD 的周长是 20 cm,以 AB,AD 为边向外作 正方形 ABEF 和正方形 ADGH,若正方形 ABEF 和正方形 ADGH 的面积之和 为 68 cm2,那么长方形 ABCD 的面积是 ( B )[来 A.21 cm2 B.16 cm2 C.24 cm2 D.9 cm2 【解析】 设 AB=x,则 AD=10-x,可得方程 x2+(10-x)2=68,解得 x1=8, x2=2,所以长方形 ABCD 的面积等于 x(10-x)=16,故选 B. 3.[2013·南京]已知如图 2-3-4 所示的图形的面积为 24.根据图中的条件,可列 出方程:__答案不唯一,如(x+1)2=25__. 图 2-3-4 4.[2012·青岛]如图 2-3-5 所示,在一块长为 22 米、宽为 17 米的长方形地面 上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行), 剩余部分种上草坪,使草坪面积为 300 平方米.若设道路宽为 x 米,则根据 题意可列出方程为__(22-x)(17-x)=300__. 图 2-3-5 5.[2012·湘潭]如图 2-3-6 所示,某中学准备在校园里利用围墙的一段,再砌 三面墙,围成一个长方形花园 ABCD(围墙 MN 最长可利用 25 m),现在已备 足可以砌 50 m 长的墙的材料,试设计一种砌法,使矩形花园的面积为 300 m2. 图 2-3-6 解:设 AB 长为 x m,由题意可得 x(50-2x)=300, 解得 x1=10,x2=15. 当 x=10 时,AD=30>25,所以 x=10 应舍去; 当 x=15 时,AD=20<25,所以 x=15 满足条件. 答:可设计矩形花园的长为 20 m,宽为 15 m. 6.[2013·连云港]小林准备进行如下操作实验:把一根长为 40 cm 的铁丝剪成两 段,并把每一段各围成一个正方形. (1)要使这两个正方形的面积之和等于 58 cm2,小林该怎么剪? (2)小峰对小林说:“这两个正方形的面积之和不可能等于 48 cm2”,他的说法 对吗?请说明理由. 解:(1)设其中一个正方形的边长为 x cm,则另一个正方形的边长为(10-x)cm. 由题意,得 x2+(10-x)2=58,解得 x1=3,x2=7. 4×3=12(cm),4×7=28(cm), 所以小林应把绳子剪成 12 cm 和 28 cm 的两段. (2)假设能围成面积之和为 48 cm2 的两个正方形,由(1),得 x2+(10-x)2=48, 化简,得 x2-10x+26=0. 因为 b2-4ac=(-10)2-4×1×26=-4<0, 所以此方程没有实数根, 所以小峰的说法是对的. 7.[2012·襄阳]为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位 准备将院内一块长 30 m,宽 20 m 的长方形空地建成一个长方形花园,要求 在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如 图 2-3-7 所示,要使种植花草的面积为 532 m2,那么小道进出口的宽度应 为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形) 图 2-3-7[ 解:设小道进出口的宽度为 x m, 依题意,得(30-2x)(20-x)=532, 整理,得 x2-35x+34=0, 解得 x1=1,x2=34. ∵34>30(不合题意,舍去), ∴x=1. 答:小道进出口的宽度应为 1 m. 8.[2012·绍兴]把一张边长为 40 cm 的正方形硬纸板进行适当地裁剪,折成一个 长方体盒子(纸板的厚度忽略不计). (1)如图 2-3-8 所示,若在正方形硬纸板的四角各剪掉一个同样大小的正方 形,将剩余部分折成一个无盖的长方体盒子. 图 2-3-8 要使折成的长方体盒子的底面积为 484 cm2,那么剪掉的正方形的边长为多 少? (2)若在正方形硬纸板的四周剪掉一些长方形(即剪掉的长方形至少有一条边 在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子.若折成的 一个长方体盒子的表面积为 550 cm2,求此时长方体盒子的长、宽、高(只需 求出符合要求的一种情况). 解:(1)设剪掉的正方形的边长为 x cm, 则(40-2x)2=484, 即 40-2x=±22,解得 x1=31(不合题意,舍去),x2=9. ∴剪掉的正方形的边长为 9 cm. (2)在如答图所示的一种裁剪图中,设剪掉的正方形的边长为 x cm,由题意, 得 第 8 题答图 2(40-2x)(20-x)+2x(20-x)+2x(40-2x)=550, 解得 x1=-35(不合题意,舍去),x2=15, ∴剪掉的正方形的边长为 15 cm. 此时长方体盒子的长为 15 cm,宽为 10 cm,高为 5 cm. 9.如图 2-3-9,在△ABC 中,∠B=90°,AB=6 cm,BC=3 cm,点 P 从点 A 开始沿 AB 边向点 B 以 1 cm/s 的速度移动,点 Q 从点 B 开始沿 BC 边向点 C 以 2 cm/s 的速度移动,如果 P,Q 分别从 A,B 同时出发. 图 2-3-9 (1)几秒钟后,P,Q 间的距离等于 4 2 cm? (2)几秒钟后,△BPQ 的面积等于△ABC 面积的一半? 解:(1)设 x 秒后 PQ=4 2 cm, 则 BP=6-x,BQ=2x, ∴(6-x)2+(2x)2=(4 2)2, 解得 x1=0.4,x2=2(舍去), ∴0.4 秒后,P,Q 间的距离等于 4 2 cm. (2)设 y 秒钟后,△BPQ 的面积等于△ABC 面积的一半, 则1 2(6-y)·2y=1 2×3×6×1 2 , 解得 y1=6-3 2 2 ,y2=6+3 2 2 (舍去)] ∴6-3 2 2 秒后,△BPQ 的面积等于△ABC 面积的一半. 10.在一块长 16 m,宽 12 m 的矩形荒地上,要建造一个花园,要求花园面积是 荒地面积的一半,下面分别是小华与小芳的设计方案,如图 2-3-10 所示. 图 2-3-10 (1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同 意见,你认为小芳的方案符合条件吗?若不符合,请用解方程的方法说明理 由; (2)你还有其他的设计方案吗?请画出你所设计的草图,将花园部分涂上阴影, 并加以说明. 解:(1)不符合条件 设小路宽度均为 x m,根据题意,得 (16-2x)(12-2x)=1 2×16×12, 解这个方程得 x1=2,x2=12, 但 x2=12 不符合题意,应舍去, ∴x=2, ∴小芳的方案不符合条件,小路的宽度应均为 2 m. (2)答案不唯一,例如: 第 10 题答图查看更多