八年级下数学课件八年级下册数学课件《勾股定理的逆定理》 人教新课标 (7)_人教新课标

八年级下数学课件八年级下册数学课件《勾股定理的逆定理》 人教新课标 (7)_人教新课标

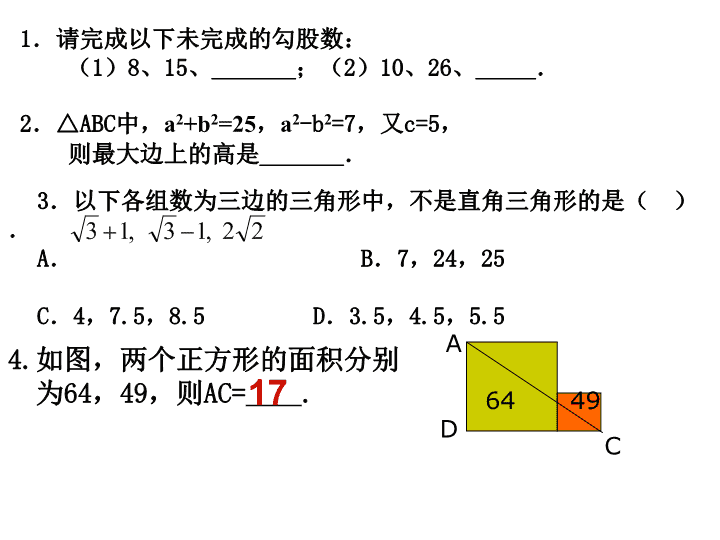
勾股定理的 逆定理 逆定理: 三角形的三边a,b,c满足a2+b2=c2,则这个三角 形是直角三角形; 较大边c 所对的角是直角. 勾股定理: 直角三角形的两直角边为a ,b , 斜边为 c ,则有 a2+ b2=c2 3．以下各组数为三边的三角形中，不是直角三角形的是 （ ）． A． B．7，24，25 C．4，7.5，8.5 D．3.5，4.5，5.5 22,13,13  1．请完成以下未完成的勾股数： （1）8、15、_______；（2）10、26、_____． 2．△ABC中，a2+b2=25，a2-b2=7，又c=5， 则最大边上的高是_______． 4.如图，两个正方形的面积分别 为64，49，则AC= . A D C 64 4917 5、如图，有一块地，已知，AD=4m， CD=3m，∠ADC=90°，AB=13m， BC=12m。求这块地的面积。 A B C 3 4 13 12 D 24平方米 6.在Rt△ABC中,∠C=90°,CD 是高,AB=1, 则 2 CD2 + AD2 +BD2 =＿＿＿＿; 7.三角形的三边长 a, b, c 满足 a2 +b2 +c2 +338 = 10a + 24b +26c, 此三角形为＿＿＿＿＿三角形. 8、如图,点A是一个半径为 400 m的圆形森 林公园的中心,在森林公园附近有 B、C 两 个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过 该森林公园?请通过计算说明. A B C 400 1000 60° 30° D 9．一艘轮船以20千米/时的速度离开港口向 东北方向航行，另一艘轮船同时离开港口以15 千米/时的速度向东南方向航行，它们离开港 口2小时后相距多少千米？ 10．已知：如图，∠ABD=∠C=90°，AD=12， AC=BC，∠DAB=30°，求BC的长． 11、如图，已知：CD⊥AB于D， 且有 求证：△ACB为直角三角形 ABADAC 2 A BD C 32CD= cm, AD=2cm, AC⊥AB。 12、已知：在四边形ABCD中，AB=3cm, BC=5cm, D CB A DC = 3.52 cm AD = 2.03 cm BC = 5.08 cm CA = 4.11 cm AB = 3.00 cm 求：S四边形ABCD D CB A DC = 3.52 cm AD = 2.03 cm BC = 5.08 cm CA = 4.11 cm AB = 3.00 cm ∵AC⊥AB(已知) ∴ AC2+AB2=BC2(勾股定理) ∵ AB=3cm,BC=5cm cmABBCAC 435 2222  又∵CD=2 cm AD=2cm(已知)3 ∴ AC2=16 , CD2+AD2=12+4=16 ∴ AC2=CD2+AD2 ∴ ∠ADC=900(勾股定理的逆定理 ∴ S四边形ABCD=S △ ABC+ S△ ACD ∴ = ×3 × 4+ × 2•2 =6+2 (cm2) = AB •AC+ AD •CD 2 1 2 1 3 3 2 1 2 1 解（1） 13、如图：边长为4的正方形ABCD中，F是DC的中点， 且CE= BC，则AF⊥EF，试说明理由 4 1 A B D C F E 解：连接AE ∵ABCD是正方形，边长是4，F是 DC的中点，EC=1/4BC ∴根据勾股定理，在 Rt△ADF，AF2=AD2+DF2=20 Rt△EFC，EF2=EC2+FC2=5 Rt△ABE，AE2=AB2+BE2=25 ∴AD=4，DF=2，FC=2，EC=1 ∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF A 边长为8和4的矩形OABC的两边分别在直角坐标 系的X轴和Y轴上，若 沿对角线AC折叠后，点B落 在第四象限B1处，设B1C交X轴于点D，求（1）三 角形ADC的面积，（2）点B1的坐标，（3）AB1 所在的直线解析式。 O C B A B1 D 1 2 3E 1、如图，在四边形ABCD中， ∠BAD=90°，AD=4，AB=3， BC=12，求正方形DCEF的面 积． 2、已知，如图，Rt△ABC中， ∠BAC=90°，AB=AC，D是BC上 任意一点， 求证：BD2+CD2=2AD2． A B C P (2)    2 1 2 100 i i i i 1 2 100 若BC边上有100个不同的点（不与B、C重合） P、P、 、P ,设m =AP +P B P C(i=1、2、 、100). 求:m +m + +m 的值。 2 2AB AP BP PC   探索与提高2： 如图所示，在△ABC中， AB=AC=4，P为BC上的一点， (1)求证：