- 2021-10-27 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版数学初中八年级上册课件-第5章- 复习课
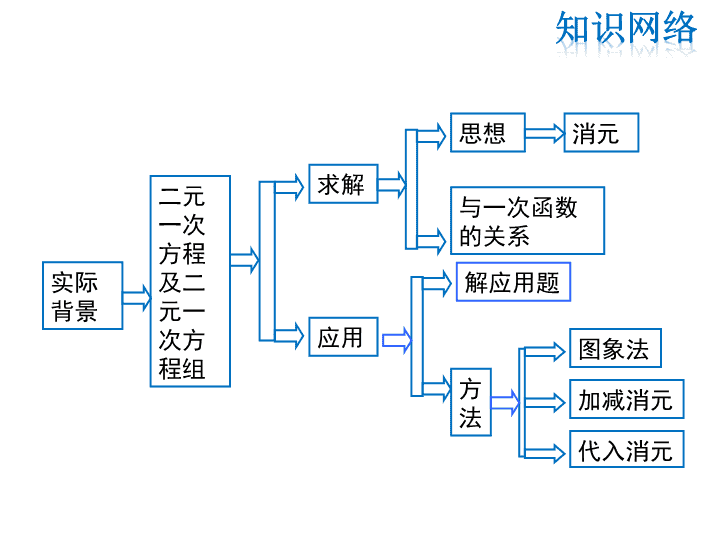
第五章 二元一次方程组 复习课 实际 背景 二元 一次 方程 及二 元一 次方 程组 求解 应用 方 法 思想 与一次函数 的关系 消元 解应用题 图象法 加减消元 代入消元 1.二元一次方程:通过化简后,只有两个未知数,并且所 含未知数的项的次数都是1,系数都不是0的整式方程, 叫做二元一次方程. 2.二元一次方程的解:使二元一次方程两边的值相等的 两个未知数的值,叫做二元一次方程的解. 3.二元一次方程组:由两个一次方程组成,共有两个未知 数的方程组,叫做二元一次方程组. 相关概念1 4.二元一次方程组的解: 二元一次方程组中各个方程的公共解,叫做二元一次 方程组的解. 5.方程组的解法 根据方程未知数的系数特征确定用哪一种解 法. 基本思想或思路——消元 常用方法————代入法和加减法 (1)求表达式:从方程组中选一个系数比较简 单的方程,将此方程中的一个未知数,如y,用 含x的代数式表示; (2)把这个含x的代数式代入另一个方程中, 消去y,得到一个关于x的一元一次方程; (3)解一元一次方程,求出x的值; (4)再把求出的x的值代入变形后的方程,求 出y的值. 用代入法解二元一次方程组2 (1)利用等式性质把一个或两个方程的两边都 乘以适当的数,变换两个方程的某一个未知数 的系数,使其绝对值相等; (2)把变换系数后的两个方程的两边分别相加 或相减,消去一个未知数,得一元一次方程; (3)解这个一元一次方程,求得一个未知数的值 ; (4)把所求的这个未知的值代入方程组中较为简 便的一个方程,求出另一个未知数,从而得到方 程组的解 . 用加减法解二元一次方程组3 审: 设: 列: 解: 答: 审清题目中的等量关系. 设未知数. 根据等量关系,列出方程组. 解方程组,求出未知数. 检验所求出未知数是否符合题意,写出答案. 列二元一次方程解决实际问题的一般步骤4 二元一次方程组和一 次函数的图象的关系 方程组的解是对应的两条直 线的交点坐标 二元一次方程和一次 函数的图象的关系 以二元一次方程的解为坐标 的点都在对应的函数图象上. 一次函数图象上的点的坐标 都适合对应的二元一次方程. 二元一次方程与一次函数5 1.关于二元一次方程2m+3n=11 正确的说法是( ) A.任何一对有理数都是它的解 B.只有两组解 C.只有两组正整数解 D.没有负整数解 C 2.若点P(x-y,3x+y)与点Q(-1,-5)关于x轴对称,则 x+y=______.3 3.已知|2x+3y+5|+(3x+2y-25)2=0, 则x-y=______.30 4.若两个多边形的边数之比是2:3,两个多边形的 内角和是1980°,求这两个多边形的边数. 解:6和9 5.方程组 中, x与y的和为12,求k的值. 253 32 kyx kyx ky kx 4 62 解得:k=14 解法1:解这个方程组,得 依题意:x+y=12 所以(2k-6) +(4-k)=12 解法2:根据题意,得 12 253 32 yx kyx kyx 解这个方程组,得k=14 6.甲、乙二人以不变的速度在环形路上跑步,如果同时 同地出发,相向而行,每隔2分钟相遇一次;如果同向而行, 每隔6分钟相遇一次.已知甲比乙跑得快,甲、乙每分钟 各跑多少圈? 解:设甲、乙二人每分钟各跑x、y圈,根据 题意得方程组 1)(6 1)(2 yx yx 解得 6 1 3 1 y x 答:甲、乙二人每分钟各跑 、 圈. 3 1 6 1 答:甲种商品的标价是20元,乙种商品的标 价是80元. 解:设甲、乙两种商品的标价分别为x、y元, 根据题意,得 ) 100 21(100) 100 51( 10 9 100 yx yx 解这个方程组,得 80 20 y x 7.已知甲、乙两种商品的标价和为100元,因市场变化,甲商品 打9折,乙商品提价5﹪,调价后,甲.乙两种商品的售价和比标价 和提高了2﹪,求甲、乙两种商品的标价各是多少? 8. 下表是某一周甲、乙两种股票的收盘价(股票每天交易结 束时的价格) 星期一 星期二 甲 12 乙 13.5 张师傅在该周内持有若干甲、乙两种股票,若按照两种股票每 天收盘价计算(不计手续费、税费行等),该人账户中星期二 比星期一多获利200元,星期三比星期二多获利1300元,试问 张师傅持有甲、乙股票各多少股? 12.5 13.3 星期三 星期四 星期五 星期六 12.9 13.9 12.45 13.4 12.75 13.15 休盘 休盘 解:设张师傅持有甲种股票x股,乙种股票y 股,根据题意,得 1300)3.139.13()5.129.12( 200)5.133.13()125.12( yx yx 解得 1500 1000 y x 答:张师傅持有甲种股票1000股,乙种股票 1500股. 9.A、B两地相距36千米.甲从A地出发步行到B地,乙从B 地出发步行到A地.两人同时出发,4小时相遇,6小时后 , 甲所余路程为乙所余路程的2倍,求两人的速度. 解:设甲、乙的速度分别为x千米/小时和y千米/小时. 依题意可得: )24(224 3644 yxxy yx 解得 5 4 y x 答:甲的速度为4千米/小时,乙的速度为5千米/小时.查看更多