八年级数学上册第15章轴对称图形和等腰三角形15-3等腰三角形（第3课时）课件（新版）沪科版

八年级数学上册第15章轴对称图形和等腰三角形15-3等腰三角形（第3课时）课件（新版）沪科版

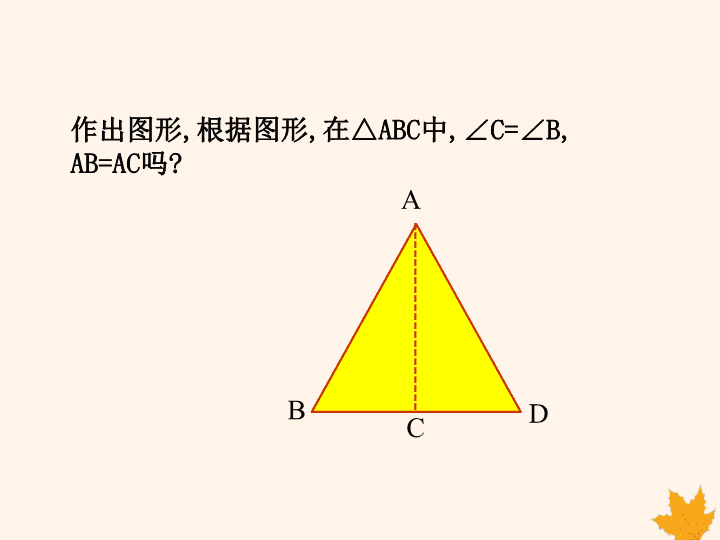
15.3 等腰三角形 第3课时 第十五章 等腰三角形的性质有哪些? 等腰三角形的两底角相等,简写为“等边对等角”. 这个命题的逆命题是什么? 等角对等边. 定理：有两个角相等的三角形是等腰三角形. 作出图形,根据图形,在△ABC中,∠C=∠B, AB=AC吗? A B C D 证明：过点A作AD⊥BC，D为垂足， ∴∠ADB=∠ADC=90°（垂直定义） 在△ADB和△ADC中， ∵∠B=∠C(已知） ∠ADB=∠ADC（已知） AD=AD(公共边） ∴△ADB≌△ADC（AAS） ∴AB=AC(全等三角形的对应边相等） 推论1：三个角都相等的三角形是等边三角形. 推论2：有一个角是60°的等腰三角形是等边三角形. 上面的定理叫做等腰三角形的判定定理，它是判断 一个三角形是否为等腰三角形的重要依据. 由上述定理可以直接得到： 如图所示，在△ABC中，∠C=90°，∠A=30°， 延长BC到点D，使CD=BC.连接AD,则△ACD≌△ACB. ∴AD=AB,∠BAC=∠DAC=30°,∠BAD=60°, ∴△ABD是等边三角形, ∴BD=AB, BC= BD= AB2 1 2 1 定理：在直角三角形中，如果一个锐角等于30°， 那么它所对的直角边等于斜边的一半. 【例】如图,一艘船从A处出发,以每小时10n mile (海里)的速度向正北航行,从A处测得一礁石C在北 偏西30°的方向上.如果这艘船上午8:00从A处出发, 10:00到达B处,从B处测得礁石C在北偏西60°的方向 上. （1）画出礁石C的位置； （2）求从B处到礁石C的距离. 60° 解：如图所示（1）以B为顶点，向 北偏西60°作角，这角一边与AC交于 点C，则点C为礁石所在地。 （2）∵∠ACB=60°-30°=30°(三角形 的外角性质） 又∵∠BAC=30° ∴∠BCA=∠BAC ∴BC=BA ∵BA=10X(10-8)=20(n mile) ∴BC=20(n mile) 即从B处到礁石C的距离是20n mile 1.已知：如图，AB交于CD于点P,CP=PD,∠A=42°， ∠CPB=138°，∠B=69°. 求证：AC=PB. 69° 138° 42° 2.已知：△ABC中AB=AC,AD平分∠BAC交BC于点D, 若∠B=45°，BC=10cm.求AD的长度. 3.已知：如图，△ABC中，∠ACB=90°， CD是斜边上的高，∠A=30°. 求BD= 1 4 AB A B C D 1.等腰三角形判定定理：有两个角相等的三角 形是等腰三角形，简称“等角对等边”. 2.推论1：三个角都相等的三角形是等边三角形. 推论2：有一个角是60°的等腰三角形是等边 三角形. 3.在直角三角形中,如果一个锐角等于30°,那 么它所对的直角边是斜边的一半.