八年级数学上册第十三章轴对称阶段自测五课件新版 人教版

八年级数学上册第十三章轴对称阶段自测五课件新版 人教版

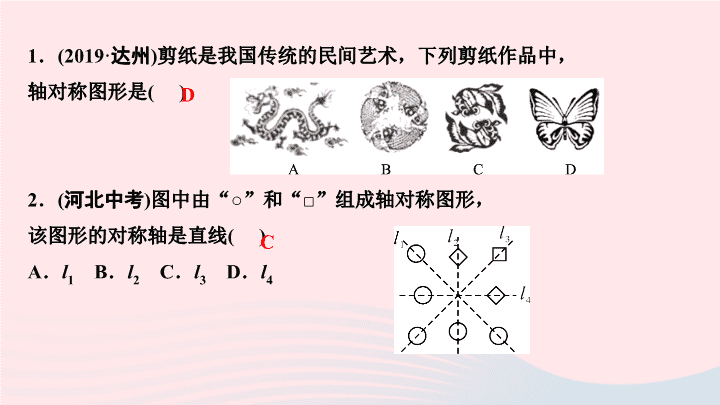
第十三章　轴对称 阶段自测(五) 1 ． (2019 · 达州 ) 剪纸是我国传统的民间艺术，下列剪纸作品中， 轴对称图形是 ( ) 2 ． ( 河北中考 ) 图中由 “ ○ ” 和 “ □ ” 组成轴对称图形， 该图形的对称轴是直线 ( ) A ． l 1 B ． l 2 C ． l 3 D ． l 4 D C 3 ． ( 贵港中考 ) 若点 A (1 ＋ m ， 1 － n ) 与点 B ( － 3 ， 2) 关于 y 轴对称， 则 m ＋ n 的值是 ( ) A ．－ 5 B ．－ 3 C ． 3 D ． 1 4 ．如图，直线 m 是五边形 ABCDE 的对称轴， 其中∠ A ＝ 130° ，∠ B ＝ 110° ，那么∠ BCD ＝ ( ) A ． 60° B ． 50° C ． 40° D ． 70° D A 5 ．如图，兔子的三个洞口 A ， B ， C 构成△ ABC ，猎狗想捕捉兔子， 必须到三个洞口的距离都相等，则猎狗应蹲守在 ( ) A ．三条边的垂直平分线的交点 B ．三个角的平分线的交点 C ．三角形三条高的交点 D ．三角形三条中线的交点 A 6 ．如图，已知 AD 所在直线是△ ABC 的对称轴，点 E ， F 是 AD 上的 两点．若 BC ＝ 4 ， AD ＝ 3 ，则图中阴影部分的面积是 ( ) A ． 3 B ． 4 C ． 6 D ． 8 7 ． (2019 · 梧州 ) 如图， DE 是△ ABC 的边 AB 的垂直平分线， D 为垂足， DE 交 AC 于点 E ，且 AC ＝ 8 ， BC ＝ 5 ，则△ BEC 的周长是 ( ) A ． 12 B ． 13 C ． 14 D ． 15 A B 8 ．如图，已知点 A (2 ， 3) 和点 B (4 ， 1) ，在坐标轴上有一点 P ， 且点 P 到点 A 和点 B 的距离相等，则点 P 的坐标为 ( ) A ． (1 ， 0) B ． (0 ，－ 1) C ． (1 ， 0) 或 (0 ，－ 1) D ． (2 ， 0) 或 (0 ， 1) C 9 ．如图所示，把一个正方形对折两次后沿虚线剪下， 展开后所得的图形是 ( ) B 10 ．如图，在 3×3 的正方形网格中有四个格点 A ， B ， C ， D ，以其中一点为原点，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是 ( ) A. A 点 B ． B 点 C ． C 点 D ． D 点 B 11 ．点 M 关于 x 轴对称的点的坐标是 ( － 1 ， 3) ， 则点 M 的坐标是 ______________ ． 12 ．如图， A ， B ， C 三点在同一条直线上，∠ A ＝ 50° ， BD 垂直平分 AE ，垂足为点 D ，则∠ EBC 的度数为 _____ ． ( － 1 ，－ 3) 100° 13 ．如图，把一张长方形的纸片 ABCD 沿 EF 折叠，点 C ， D 分别落在 C ′ ， D ′ 的位置上， EC ′ 交 AD 于点 G ， 已知∠ EFG ＝ 56° ，那么∠ BEG ＝ _____ ． 14 ．如图，在正方形方格中，阴影部分是涂黑 7 个小正方形 所形成的图案，再将方格内空白的一个小正方形涂黑， 使得到的新图案成为一个轴对称图形的涂法有 ___ 种． 68° 3 15 ．如图，在△ ABC 中， BC 边上的垂直平分线 DE 交边 BC 于点 D ， 交边 AB 于点 E . 若△ EDC 的周长为 24 ， △ ABC 与四边形 AEDC 的周长之差为 12 ，则线段 DE 的长为 ____ ． 6 三、解答题 ( 共 40 分 ) 16 ． (8 分 ) 如图，△ ABC 在平面直角坐标系中， 其中，点 A ， B ， C 的坐标分别为 A( － 2 ， 1) ， B( － 4 ， 5) ， C( － 5 ， 2). (1) 作△ ABC 关于 y 轴对称的△ A1B1C1 ， 其中，点 A ， B ， C 的对应点分别为 A1 ， B1 ， C1 ； (2) 写出点 A1 ， B1 ， C1 的坐标． 解： (1) 如图所示， △ A 1 B 1 C 1 即为所求　 (2) 点 A 1 ， B 1 ， C 1 的坐标分别为 (2 ， 1) ， (4 ， 5) ， (5 ， 2) 17 ． (10 分 ) 如图，某校两个班的学生分别在 C ， D 两处参加植树活动，现要在道路 AO ， OB 的交叉区域内设一个茶水供应点 M ，使点 M 到两条路的距离相等，且 MD ＝ MC ，这个茶水供应点应建在何处？ 解：作法：①连接 CD ，作 CD 的垂直平分线 EF ； ②作∠ AOB 的平分线 OP ， OP 与 EF 相交于点 M ，则点 M 就是所求作的点 18 ． (10 分 ) 如图， AD 是 ∠ BAC 的平分线， DE ⊥ AB ， DF ⊥ AC ， 垂足分别为点 E ， F ，连接 EF ， EF 交 AD 于点 G ，求证： AD 垂直平分 EF . 19 ． (12 分 ) 如图所示，点 P 在∠ AOB 的内部，点 M ， N 分别是点 P 关于直线 OA ， OB 的对称点，线段 MN 交 OA ， OB 于点 E ， F . (1) 若 MN ＝ 20 cm ，求△ PEF 的周长； (2) 若∠ AOB ＝ 35° ，求∠ EPF 的度数． 解： (1) ∵ 点 M 与点 P 关于 OA 对称， ∴ OA 垂直平分 MP . ∴ EM ＝ EP . 又 ∵ 点 N 与点 P 关于 OB 对称， ∴ OB 垂直平分 PN . ∴ FP ＝ FN . ∴△ PEF 的周长为 PE ＋ PF ＋ EF ＝ ME ＋ FN ＋ EF ＝ MN ＝ 20 cm 　 (2) 连接 OM ， ON ， OP . ∵ OA 垂直平分 MP ， ∴ OM ＝ OP . 又 ∵ OB 垂直平分 PN ， ∴ ON ＝ OP . 又 ∵ ME ＝ PE ， OE ＝ OE ， PF ＝ NF ， OF ＝ OF ， ∴△ MOE ≌△ POE (SSS) ， △ POF ≌△ NOF (SSS). ∴∠ MOE ＝ ∠ POE ， ∠ OME ＝ ∠ OPE ， ∠ POF ＝ ∠ NOF ， ∠ OPF ＝ ∠ ONF . ∴∠ MON ＝ 2 ∠ AOB ＝ 70°. ∴∠ EPF ＝ ∠ OPE ＋ ∠ OPF ＝ ∠ OME ＋ ∠ ONF ＝ 180° － ∠ MON ＝ 110°