菱形的性质教案1

菱形的性质教案1

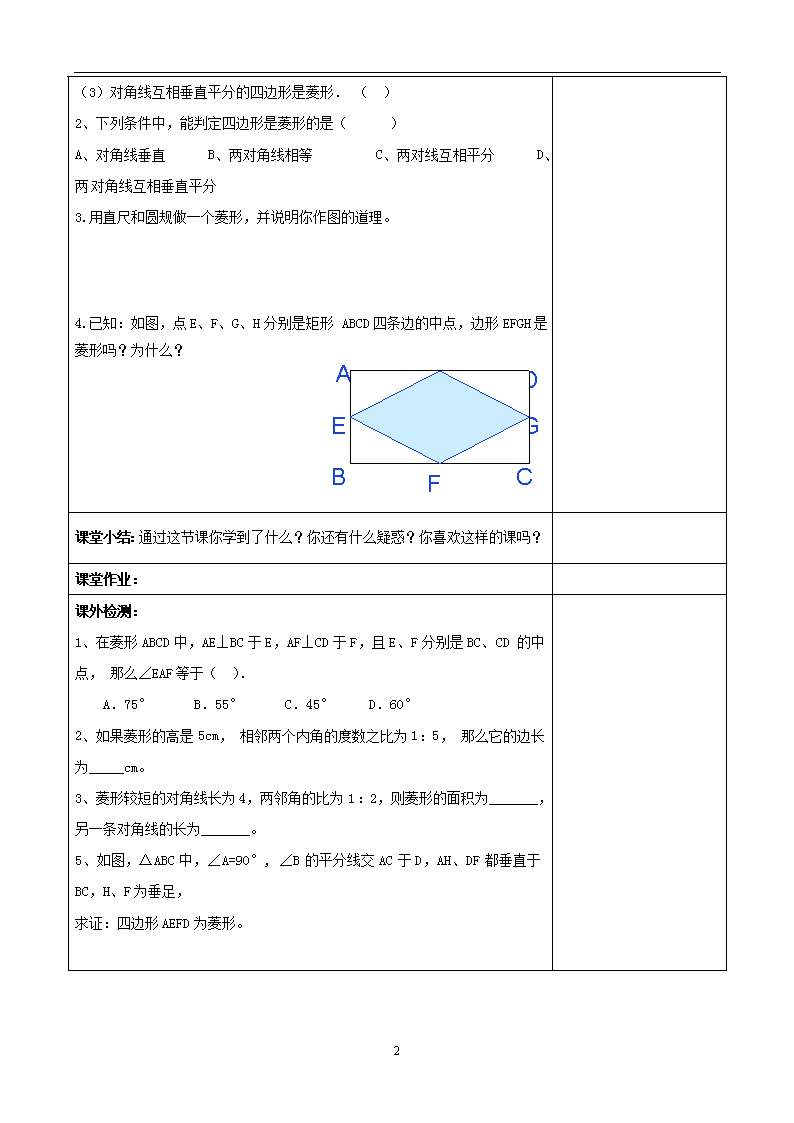
‎ 菱形的判定 教学目标 ‎1．经历菱形的判定定理的发现过程。‎ ‎2．掌握菱形的判定定理“四条边相等的四边形是菱形”。‎ ‎3．掌握菱形的判定定理“对角线互相垂直的平行四边形是菱形”。‎ 教学重点 经历菱形的判定定理的发现过程 教学难点 菱形判定定理的灵活运用 教学过程 二次备课及设计思路 1、 情境创设：‎ 我们知道，菱形的四条边相等。反过来，四边相等的四边形是菱形吗？‎ 我们知道，当平移一个平行四边形活动框架的一边，使这个平行四边形成菱形时，它的两条对角线互相垂直。反过来，对角线互相垂直的平行四边形是菱形吗？‎ ‎2、总结结论： _____________四边形是菱形。_______________________的平行四边形是菱形。‎ ‎3、例1、如图，平行四边形ABCD的两条对角线AC，BD相交于点O，OA=3，OB=4，AB=5，（1）AC，BD互相垂直吗？为什么？‎ ‎（2）四边形ABCD是菱形吗？为什么？‎ ‎4、例2、如图，在四边形ABCD中，AD∥BC，对角线AC的垂直平分线与边AD、BC分别交于点E、F，‎ 四边形AFCE是菱形吗？为什么？‎ 当堂检测：‎ ‎1、判断题（对的打“∨”，错的打“×）：‎ ‎（1）有一组邻边相等的四边形是菱形；（ ） ‎ ‎（2）对角线互相垂直的四边形是菱形； （ ）‎ 3‎ ‎（3）对角线互相垂直平分的四边形是菱形． （ ）‎ ‎2、下列条件中，能判定四边形是菱形的是（　　　）‎ A、对角线垂直　 B、两对角线相等 C、两对线互相平分 　D、两对角线互相垂直平分 ‎3.用直尺和圆规做一个菱形，并说明你作图的道理。‎ A B G D C E F ‎4.已知：如图，点E、F、G、H分别是矩形 ABCD四条边的中点，边形EFGH是菱形吗？为什么？‎ 课堂小结：通过这节课你学到了什么？你还有什么疑惑？你喜欢这样的课吗？‎ 课堂作业：‎ 课外检测：‎ ‎1、在菱形ABCD中，AE⊥BC于E，AF⊥CD于F，且E、F分别是BC、CD的中点，那么∠EAF等于（ ）．‎ ‎ A．75° B．55° C．45° D．60°‎ ‎2、如果菱形的高是5cm，相邻两个内角的度数之比为1：5，那么它的边长为_____cm。‎ ‎3、菱形较短的对角线长为4，两邻角的比为1：2，则菱形的面积为_______，另一条对角线的长为_______。‎ ‎5、如图，△ABC中，∠A=90°, ∠B的平分线交AC于D，AH、DF都垂直于BC，H、F为垂足，‎ 求证：四边形AEFD为菱形。‎ 3‎ ‎ ‎ ‎6、如上右图，在矩形ABCD中，对角线AC的垂直平分线与AD，BC分别交于点E，F 。试说明：四边形AFCE是菱形。‎ 板书设计 教后反思 3‎