八年级下数学课件《二次根式》 (14)_苏科版
⑵什么是一个数的算术平方根?如何表示?
正数的正的平方根叫做它的算术平方根。
⑴什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则
这个数就叫做a的平方根。
用 (a≥0)表示。a
0的算术平方根平方根是0
a的平方根是 a
复习
1、如果 ,那么 ;42 x x
2、如果 ,那么 ;32 x x
3、如果 ,)0(2 aax
x那么 。
±2
3
a
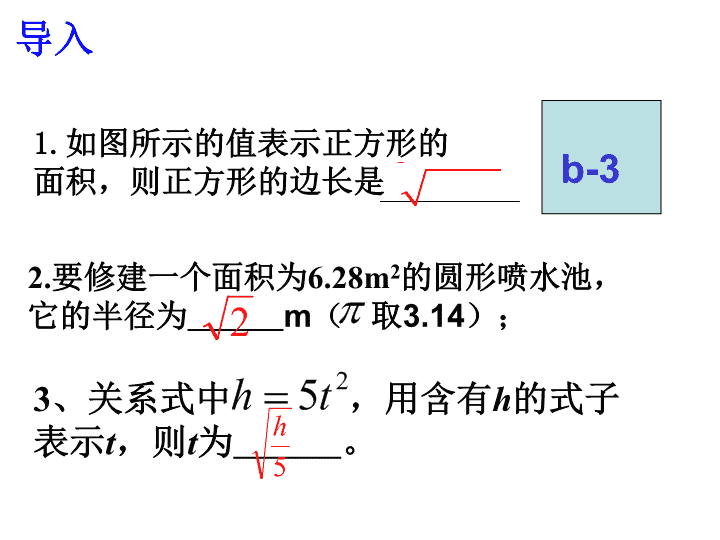
1.如图所示的值表示正方形的
面积,则正方形的边长是 3b b-3
2.要修建一个面积为6.28m2的圆形喷水池,
它的半径为 m( 取3.14);2
3、关系式中 ,用含有h的式子
表示t,则t为 。
25th
5
h
导入
新授:
观察以上各式,它们有什么共同特点?
表示一些正数的算术平方根
3b 2 5
h
25002 a
25002 a 3b
表示一些正数的算术平方根.
.的式子叫做二次根式形如 a )0( a
你认为所得的各代数式有哪些共同特点?
a 被开方数
二次根号
2 5
h
归纳:
二次根式的定义(默1)
一般地,形如 的式子
叫二次根式。
)0( aa
本课学习目标:
(1)二次根式的概念( 双
重非负性)
• (2)根号内字母的取值范围
• (3)二次根式的性质(1,2)
请你凭着自己已有的知识,说
说对二次根式 的认识!a
?
( 0) .a a 形如 的式子叫做二次根式
2. a可以是数,也可以是式.
3. 形式上含有二次根号
4. a≥0, ≥0 a
5.既可表示开方运算,也可表示运算的结果.
1.表示a的算术平方根
( 双重非负性)
1a如: 这类代数式只能称为含有二次根
式的代数式,不能称之为二次根式;
而
这类代数式,应把 这些二次根式看
做系数或常数项,整个代数式仍看做整式。
322 2 xx
3,2
说一说:
下列各式是二次根式吗?
32 5 (7) , a (6)
, xy (5) m-(4)
,12 (3) 6, (2) ,32 (1)
1
(m≤0), (x,y 异号)
在实数范围内,负数没有平方根
2
1
9a
222 aa x )0( x
23m
1、判断下列代数式中哪些是二次根式?
⑴ ⑵
⑶ ⑷
⑸ 1 ( 3)a a ⑹
16
例1 x为何值时,下列各式在实数范围内有意义。
(1) 5x (2) 1 3x (3) 1 3x x
例题讲解
(3)由题意可知:
5x
03
01
x
x
1
3
1 3x x
1
3
1 3x
1
5x
1)由x-5≥0,得x ≥5
∴当 x ≥5时, 有意义
(2)由1-3x≥0得x≤
∴当 x ≤ 时, 有意义
∴当 -1≤ x ≤3时, 有意义;
解:(
变式:
1
5x
5 0
1 0
5
x
x
1
5x
当x取何值时, 在实数范围内有意义。(默2)
∴ 当x>5时, 在实数范围内有意义。
x-5 0解:由题意得
5
1
x
2x
1
-5
解:由题意得,
2 0
2 0
2 0
2
x
x
x
x
5
5
5
5
(默3)
求下列二次根式中字母 的取值范围(默4)
(1)解:
字母 a 的取值范围是全体实数
a
(1)
∵无论 取何值,
都有
a
21 0a
∴字母 的取值范围是全体实数.a
a∴字母 的取值
范围是全体实数.
2
2
2
2 2
( 2 1) 1
( 1) 1 0
a a
a a
a
∵
2a 2)1( a(2) 2a
(2)解: - 02 a
0
02
a
a
02 a
2)1( a
(a为任何实数)
(a=1)
说明:1.当被开方数本身为非负数或能化为非负
数形式时,其字母的取值范围为:全体实数;
2.当被开方数本身为非正数或能化为非正数形式
时,其字母的取值范围为:使被开方数为0的值。
(a为任何实数)
求下列二次根式中字母的取值范围:
11 a
a21
12
233 a
解:(1)由题意得:
1 0a 1a
即当 时, 1a 1a 有意义.
求字母的取值范围的口诀(默5)
从左看到右;从上看到下
看到分数线,分母不为0
(2) (3) 为任意实数a1
2
a 看到偶次根式,被开方数大于等于0
看到0指数,底数不为0
最后画数轴,写出解集来
x
x 1)4(4)3( 2
1、 x取何值时,下列二次根式有意义?
xx 3)2(1)1( 1x 0x
为全体实数x 0x
3)5( x 0x
2
1)6(
x
0x
01 ( 2)
3
x x
x
(7) 1, 2x x 且
2x
x
(8) 0x 1)9( 2 x 为全体实数x
参考图1-2,完成以下填空:
2
2 2 12 _____; 7 _____; _____.
2
2 7
1
2
一般地,二次根式有下面的性质:
快
速
判
断
2 2
2
2
2
2 11 3 ______, 2 ______, 3 2 ________,
7 3
24 5 ________, 5 ________.
3
5
3
2
7
12
3
2
3
a
a
?
941657
)0(2 aaa
aa 2)(
2
2
2
2 ___,
5 ___,
0 ___,
| 2| ___;
| 5| ___;
| 0| ___.
请比较左右两边的式子,议一议: 与 有什么关
系?当 时, ;当 时,
2a | |a
2 ____;a 2 ____.a 0a 0a
22
5 5
00
a a
)0(
0(2
aa
aaaa )
aa 2
2)2)(1(
2)2)(2(
2)2()3(
2)2()4(
22)5(
2)2()6(
2
2
-2
|-2|=2
|2|=2
-|-2|=-2
大
家
抢
答
23 ______
2
2 ______,
7
25 ________
21 _____
22 ______
5
1
3
2
5
2
7
5
1
2
5
24 _________ 4 4
2
1 ( 1)x x 1x
?)( 22 有区别吗与 aa
2.从取值范围来看,
2a
2a
a≥0
a取任何实数
1:从运算顺序来看,
2a
2a
先开方,后平方
先平方,后开方
=a
a (a≥ 0)
3.从运算结果来看:
2a
2a
-a (a<0)
==∣ a∣
比较分析 和 2a 2
a
读法
运算顺序
a的取值范围
运算结果
2
a 2a
先开方,后平方 先平方,后开方
a≥0 a取全体实数
a ∣ a∣
根号a的平方 根号下a平方
二次根式的性质及它们的应用:
(1)
(2)
2a a
a
0
-a
( a >0 )
( a =0 )
( a <0 )
(默6)
)0(,
2
aaa aa 2)(
2
211
(x﹤y)21: 原式解
212 x
1: x原式解
(x>0 )
讨论与思考
将下列各式化简:
)21(
)1( x原式
12
1 x
2)(: yx 原式解
xy
22 23 yxyx
01
0
0
x
x
x
yx
yx
0yx
)yx (原式
42
例3、化简及求值:
(1) (2) (3) (a<0,b>0)
(⑷) 其中a=
(5)
4a 2 2a b
21 2a a
22 )12()21(
3
42(1) (2) (3) (a<0,b>0)
(⑷) 其中a=
(5)
4a 2 2a b
21 2a a
22 )12()21(
422 解:原式
22 aa 解:原式 ab解:原式
1)1(: 2 aa原式解
221212
1221
解:原式
0,0 ba
0ab
ab原式
3
1313133 )(时,原式当a
解:原式= 2 2( 3) ( 1)x x
=|x-3|+|x+1|
∵-1
0
∴原式 = (3-x) + (x+1) = 4
_________
,4)4( 2
的取值范围是则
思考:若
m
mm
mm 4?)4( 2
4m
4
04
m
m
41682 mmm
(默7)
(默8)
1.若 ,则x的取值范围为 ( )xx 1)1( 2
(A) x≤1 (B) x≥1 (C) 0≤x≤1 (D)一切有理数
A
2.实数a、b、c在数轴上的位置如图所示,化简
2 2( ) ( )a b b c c a
a b c
2( )b c a 2( )c a b 2( )b c a
3.已知a,b,c为△ABC的三边长,化简:
+ -
0)(,0)(,0
,,,
acbbacacb
cba
是三角形三边
这一类问题注意把二次根式的运算搭载在三角形三边之间的关系
这个知识点上,特别要应用好。
acbbacacb 解:原式
cab
acbcbaacb
3
原式
(默9)
化简 xx 1)31 2(
4.化简
22 2)1( pp
)2(1 pp 解:原式
1
21
pp
2
02
p
p
22 )()1( aa
aa 1解:原式
12
1
a
aa
3
1
031
x
x
(默10)
归纳
二次根式的非负性:
0a
二次根式的双重非负性:
0
0
a
a
a
( ) ( ),
时,、当
yx
yx 0311
的值。求
、已知
xyz
zyx 023652 2
3.根据非负数的性质,就可以确定字母的值.
2.如果几个非负数的和为零,那么每一个非负数都为零.
到现在为止,我们已学过哪些数非负数形式?
思考:
为偶数)nan ( )0( aaa
的双重非负性再议 a
非负数
的性质:
1.几个非负数的和、积、商、乘方及
算术平方根仍是非负数
cbacba 则若( ,023)2 2
3
(默11)
(默11)
(默11)
例3、当x是怎样的实数时, 有最
小值?最小值是多少?
2x
2
02
x
x
有什么性质?
二次根式 的双重非负性:a
0
0
a
a
a
02 x解:
02 x2x
当x= -2时,
有最小值02x
2、2+ 的最小值为__,此时x的值为
__。
x3 2
3
(默12)
当t是怎样的实数时, 有最
小值?最小值是多少?
012 t解:
12 t
不可能)(1
01
2
2
t
t
11
11
0
2
2
2
t
t
t
当t=0时,
有最小值1
12 t
(默13)
小结:
1.怎样的式子叫二次根式?
2.怎样判断一个式子是不是二次根式?
3.如何确定二次根式中字母的取值范围?
.的式子叫做二次根式形如 a )0( a
(1). 形式上含有二次根号
(2).被开方数a为非负数,
从左看到右;从上看到下
看到分数线,分母不为0
看到偶次根式,被开方数大于等于0
看到0指数,底数不为0
最后画数轴,写出解集来
4.真正理解: )0(
2
aaa
aa2 )0(
)0(
aa
aa
这两个性质的概念,
我们才能灵活地去解决有关二次根式的问题。
解决二次根式类问题时特别注意条件,
有时还得挖掘隐含条件。
(双重非负性).0,0.5 aa
二次根式的性质及它们的应用:
(1)
(2)
2a a
a
0
-a
( a >0 )
( a =0 )
( a <0 )
)0(,
2
aaa
3.根据非负数的性质,就可以确定字母的值.
2.如果几个非负数的和为零,那么每一个非负数都为零.
到现在为止,我们已学过哪些数非负数形式?
思考:
为偶数)nan ( )0( aaa
的双重非负性再议 a
非负数
的性质:
1.几个非负数的和、积、商、乘方及
算术平方根仍是非负数
cbacba 则若( ,023)2 2 3
切入点:从字母的取值范围入手。
l1.已知 ,你能求出 的值吗?4 4 2y x x x y
l3.已知 ,你能求出 a 的取值范围吗?
1
3
x
x
l2.已知 与 互为相反数,
求 、 的值.
2 9x y 3x y
x y
切入点:从代数式的非负性入手。
l4.已知 为一个非负整数,试求非负整数 的值10 a a
切入点:分类讨论思想。
(4)
1
a
a
0
1
1 0
0 0
或
1 0 1 0
1或 0
a
a
a
a a
a a
a a
解:由题意得,
(4)
1
a
a
2.已知a,b为实数,且满足
,你能求出a及
a+b 的值吗?
12112 bba
2ab1.若 =0,则 =_____。
3、已知 有意义,那A(a, )在 象限.二
a
1
∵由题意知a<0 ∴点A(-,+)
a
2 2( 5) (2 2)a b 5
.
,12
的值求自然数
为一个整数
n
n
可以为:a 12、11、 8、 3
1、求下列二次根式中字母的取值范围:
(1) (2) (3) (4)
4 3x
2 1x
1x2
2
+
22y )-(1 3
2
x
1 3 0
2
1
6
x
x
(1)解:由题意得,
2( 2) 0y
y
可取全体实数
(2)解:由题意得,
2 1 0
1
2
x
x
(3)解:由题意得, 4 3 0
2 1
2 1 0
4 3 0 4 3 0
或
2 1 0 2 1 0
4 1
3 2
x
x
x
x x
x x
x
(4)解:由题意得,
2x
1
-
0
2 0
0且 4
x
x
x x
解:由题意得,
1. 求下列各式有意义时的X取值范围:
| | 3
1 4
x
x
| | 3 0
1 4
1 4 0
| | 3 0 | | 3 0
或
1 4 0 1 4 0
3或 3 3 3
或1 1
4 4
13或 3
4
x
x
x
x x
x x
x x x
x x
x x
解:由题意得,
112 xx
xx 631
23 2 x 14 x
_______)3)(2(______)1()1( 22
______)4()4(______)3
11()3( 22
11
3 4
31
2.数a在数轴上的位置如图,
则 2 _____ .a
0-2 -1 1
aa
1.填空
____;)1()5( 22 x ;__________)6( 2 m12 x )0(
)0(
mm
mm
3.实数p在数轴上的位置如图所示,
化简
22 2)1( pp
1
21
)2(1
pp
pp
2 2( 4) ( 1)x x
2 2 2 2( ) ( ) ( ) ( )a b c a b c b a c c b a
6.x,y取怎样的实数时,下列各式在实数
范围内有意义?
(1) xy 2 2(2) x y
解(:1)由题意得,
-xy 0, 即xy 0
, 0
,
x y
x y
是异号,两数都为 ,
或 中至少有一个数为0
,x y(2) 中至少有一个数为0时, 2 2x y 有意义
1.(2010·芜湖中考)要使式子 有意义,
a的取值范围是( )
A. a≠ 0 B. a>-2且a≠ 0
C. a>-2或a≠ 0 D. a≥-2且a≠ 0
【解析】选D.要使式子 有意义,须同时
满足a+2≥0,a≠0两个条件,解两个不等式
可得a≥-2且a≠0 。
a
a 2
a
a 2
2.下列式子一定是二次根式的是( )
A. B. C. D.
【解析】选C.A中只有当x≤-2时,才是二次根式,故A不一
定是二次根式;B中当x≥0时是二次根式,故B不一定是二
次根式;C中无论x为何值,x2+2>0,所以C一定是二次根
式;D中当x=0时,不是二次根式,所以D也不正确。
2x x 2 2x
2 2x
若a.b为实数,且
求 的值。
| 2 | 2 0a b
2 2 2 1a b b
解:
2 0,a 2 0b
而 2 2 0a b
2 0,a 2 0b
2, 2a b
2 22 2原式 1 1 2 1 3a b a b
3.
2(1 2) 2( 2 3) 2( 3 4)4..计算: + + +…+
2)20112010(
5.如果 2( 5)a +│b-2│=0,求以a、b为边长的等腰
三角形的周长。
12011
20102011...342312
解原式
12
2,5,02)5( 2
的周长为
解
ABC
baba
2( 3)x 2 x6.化简: -( )2
.
分析:本题是化简,说明题中的每一个二次根式均在有意
义的范围内,本题有一个隐条件,即2-x≥0,x≤2.
123,2,02 xxxx 原式解
( ) ( )a x a a y a x a a y
2 2
2 2
3x xy y
x xy y
7.设等式
在实数范围内成立,其中a, x, y 是两两不等的实数,求
的值。 解:∵ ( ) ( )a x a a y a x a a y
3
13,,,0 22
22
yxyx
yxyxyxyxa
巩固提高:
2( 3 2 )x
1.分别求下列二次根式中的字母的取值范围
2(1 )x 3
2
x
x
(1) (2) (3)
2
3023).1( xx 为全体实数x).2(
23203).3( xxxx 且且
2.当x_____时, 3 3x x 有意义.=0
22( ) 2 ( )a b b a 3.化简: =______2a-3b
4.要使式子 有意义,那么x的取值范围是( )
A、x>0 B、x<0 C、x=0 D、x≠0
x x C
3 3 2y x x 3y x5.已知 ,求 的值。
393
2,3,33,0303
2
y x
yxxxxx 只有且且解
0xy 2x y6.已知 ,化简:
yxyxyxyxxy 22 ,0,0:0,0 得解由
7 3, 7 3x y 2 2x xy y 7.已知: ,求 的值。
1612283)(
4,72
222
xyyxyxyx
xyyx
解
练习:1.用心算一算:
24
7
1
2101
2
7
12
2
233
0.1
18
2
32)5( 12
2
326 23
2.计算:
22 )15()10()1( 222])2(2[)2( 2
)9(25)7()3( 2 22 )
7
3
5
4()
5
3
7
2()4(
51510 解原式
222222
22222
解原式
15357 解原式
35
2
7
1
5
1
7
3
5
4
7
2
5
3
解原式
22
2
2
1 1 0 1 5 ;
2 7 2 5 9 ;
3 2 2 2 2 2 .
试试你的计算能力:
2
15
-5
试试你的计算能力:
2
2 2
3 2 4 21 | |;
5 3 5 3
2 3 4 32 .
7 5 5 7
15
23
35
2
把下列各式写成平方差的形式, 再在
实数范围内分解因式;
54)1( 2 x 103)2( 2 a
22 52)1( )()(原式解、 x
22 103)2( )()(原式 a
)52)(52( xx
)103)(103( aa
思路启迪:利用 可以把任何一
个非负数或非负式子写成完全平方形式.
0
2
aaa
把下列各式写成平方差的形式, 再在
实数范围内分解因式;
9)3( 4 a 96)4( 24 aa
222 3)3( )(原式 a
22 )3()4( a原式
)3)(3( 22 aa
)3)(3)(3( 2 aaa
22 )3()3( aa
.,18 的值求自然数为一个整数 nn
n为2,9,14,17
1( 2 )
1 2 a
1 0
1 2
1 2 0
1 2 0
1
2
a
a
a
a
解:由题意得,