八年级数学上册第十二章全等三角形12-2三角形全等的判定第2课时边角边教学课件新版 人教版

八年级数学上册第十二章全等三角形12-2三角形全等的判定第2课时边角边教学课件新版 人教版

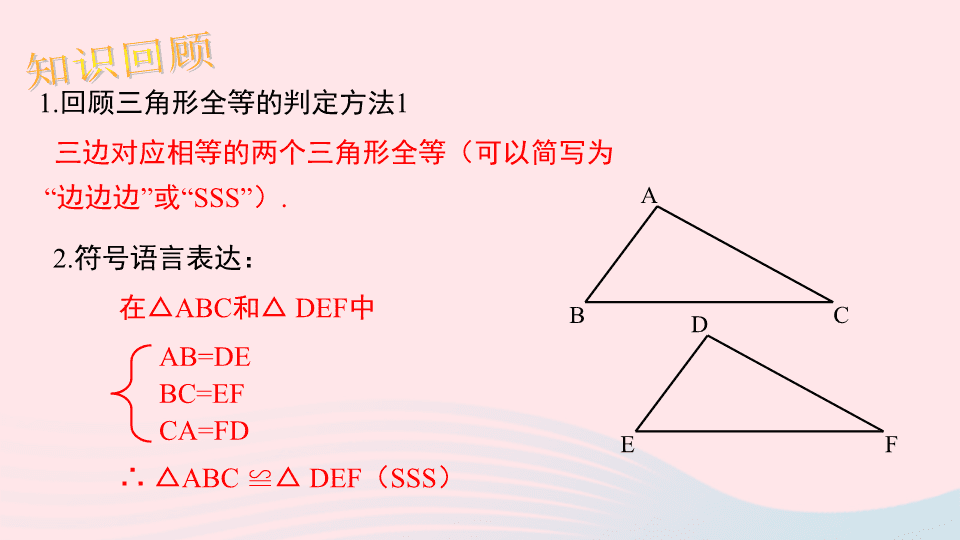
12.2 三角形 全等 的判定 第十二章 全等三角形 第 2 课时 “边 角 边” 情境引入 学习目标 　 1 ． 探索并正确理解三角形全等的 判定方法 “ SAS ” . （重点） 　 2 ． 会用“ SAS ” 判定方法证明两个三角形全等及进行简单的应用．（重点） 3. 了解“ SSA ” 不能作为两个三角形全等的条件．（难点） 　 1. 回顾三角形全等的判定方法 1 三边对应相等的两个三角形全等（可以简写为 “边边边”或“ SSS” ） . 在△ ABC 和△ DEF 中 ∴ △ ABC ≌ △ DEF （ SSS ） AB=DE BC=EF CA=FD 2. 符号语言表达： A B C D E F 知识回顾 当两个三角形满足六个条件中的 3 个时，有四种情况 : 三角 × 三边 √ 两边一角 ？ 两角一边 除了 SSS 外 , 还有其他情况吗？ 思考 讲授新课 三角形全等的 判定（ “ 边角边 ” 定理） 一 问题： 已知一个三角形的两条边和一个角，那么这两条边与这一个角的位置上有几种可能性呢？ A B C A B C “ 两边及夹角 ” “ 两边和其中一边的对角” 它们能判定两个三角形全等吗？ 尺规作图画出一个 △ A′B′C′ ，使 A′B′ ＝ AB ， A′C′ ＝ AC ，∠ A ′ ＝∠ A （即使两边和它们的夹角对应相等） . 把画好的 △ A′B′C′ 剪下，放到 △ ABC 上，它们全等吗？ A B C 探究活动 1 ： SAS 能否判定 的两个三角形全等 动手试一试 A B C A ′ D E B ′ C ′ 作法： （ 1 ）画 ∠ DA ' E =∠A ； （ 2 ）在射线 A'E 上截取 A'C'=AC , 在射线 A'D 上截取 A'B'=AB ； （ 3 ）连接 B ' C '. ？ 思考： ① △ A′ B′ C′ 与 △ ABC 全等吗？如何验证？ ② 这两个三角形全等是满足哪三个条件？ 在 △ ABC 和 △ DEF 中， ∴ 　 △ ABC ≌ △ DEF （ SAS ）． 文字语言： 两边和它们的夹角分别相等的两个三角形全等 （简写成 “边角边 ” 或“ SAS ” ）． 知识要点 “边角边”判定方法 几何语言： AB = DE ， ∠ A = ∠ D ， A C = A F ， A B C D E F 必须是两边“夹角” 例 1 ： 如果 AB = CB ，∠ ABD = ∠ CBD ， 那么 △ ABD 和 △ CBD 全等吗？ 分析 : △ ABD ≌ △ CBD . 边 : 角 : 边 : AB=CB ( 已知 ) ， ∠ ABD = ∠ CBD ( 已知 ) ， ？ A B C D (SAS) BD=BD ( 公共边 ). 典例精析 证明： 在 △ ABD 和 △ CBD 中， AB=CB ( 已知 ) ， ∠ABD= ∠CBD ( 已知 ) ， ∴ △ ABD ≌ △ CBD ( SAS). BD=BD ( 公共边 ) ， 变式 1: 已知：如图 ,AB=CB,∠1= ∠2. 求证 :(1) AD=CD ； (2) DB 平分 ∠ ADC. A D B C 1 2 4 3 在 △ABD 与 △CBD 中， 证明 : ∴△ABD ≌ △CBD （ SAS ）， AB=CB ( 已知）， ∠1=∠2 （已知）， BD=BD （公共边）， ∴AD=CD ， ∠3=∠4 ， ∴DB 平分 ∠ ADC. A B C D 变式 2: 已知 :AD=CD ， DB 平分 ∠ADC ，求证 :∠A=∠C. 1 2 在 △ABD 与 △CBD 中， 证明 : ∴△ABD ≌ △CBD （ SAS ）， AD=CD ( 已知）， ∠1=∠2 （已证）， BD=BD （公共边）， ∴ ∠ A =∠ C. ∵DB 平分 ∠ ADC ， ∴ ∠1=∠2. 例 2 ： 如图，有一池塘，要测池塘两端 A 、 B 的距离，可先在平地上取一个可以直接到达 A 和 B 的点 C ，连接 AC 并延长到点 D ，使 CD ＝ CA ，连接 BC 并延长到点 E ，使 CE ＝ CB ．连接 DE ， 那么量出 DE 的长就是 A 、 B 的距离，为什么 ? C · A E D B 证明：在 △ ABC 和 △ DEC 中， ∴ △ ABC ≌ △ DEC （ SAS ）， ∴ AB =DE ， （ 全等三角形的对应边相等 ） . AC = DC （ 已知 ）， ∠ ACB = ∠ DCE （ 对顶角相等 ）， CB = EC （ 已知 ） ， 证明线段相等或者角相等时，常常通过证明它们是全等三角形的对应边或对应角来解决 . 归纳 已知 : 如图 , AB=DB,CB=EB ,∠1 ＝∠ 2 ， 求证 : ∠ A =∠ D . 证明 :∵ ∠1 ＝∠ 2( 已知 ) ， ∴∠1+∠ DBC ＝ ∠ 2+ ∠ DBC ( 等式的性质 ) ， 即 ∠ ABC ＝∠ DBE . 在 △ ABC 和 △ DBE 中 , AB ＝ DB ( 已知 ) ， ∠ ABC ＝∠ DBE ( 已证 ) ， CB ＝ EB ( 已知 ) ， ∴△ ABC ≌ △ DBE (SAS). ∴ ∠ A =∠ D ( 全等三角形的对应角相等 ). A 1 2 C B D E 针对训练 　想一想： 如图，把一长一短的两根木棍的一端固定在一起，摆出 △ ABC . 固定住长木棍，转动短木棍，得到 △ ABD . 这个实验说明了什么？ B A C D △ ABC 和△ ABD 满足 AB = AB , AC = AD , ∠ B = ∠ B , 但△ ABC 与△ ABD 不全等 . 探究活动 2 ： SSA 能否判定两个三角形全等 画一画 ： 画 △ ABC 和 △ DEF ，使 ∠ B =∠ E =30° ， AB = DE =5 cm ， AC = DF =3 cm ．观察所得的两个三角形是否全等？   A B M C D A B C A B D 有两边和其中一边的对角分别相等的两个三角形不一定全等 . 结论 例 3 下列条件中，不能证明△ABC ≌ △DEF的是(　　) 典例精析 A． AB ＝ DE，∠B ＝ ∠E，BC ＝ EF B． AB ＝ DE，∠A ＝ ∠D，AC ＝ DF C． BC ＝ EF，∠B ＝ ∠E，AC ＝ DF D． BC ＝ EF，∠C ＝ ∠F，AC ＝ DF 解析：要判断能不能使 △ ABC ≌ △ DEF ，应看所给出的条件是不是两边和这两边的夹角，只有选项 C 的条件不符合，故选 C. C 方法总结： 判断三角形全等时，注意两边与其中一边的对角相等的两个三角形不一定全等．解题时要根据已知条件的位置来考虑，只具备 SSA 时是不能判定三角形全等的． 当堂练习 1. 在下列图中找出全等三角形进行连线 . Ⅰ ر 30 º 8 cm 9 cm ر 30 º 8 cm 8 cm 8 cm 5 cm Ⅲ ر 30 º 8 cm 8 cm Ⅲ ر 30 º 8 cm 9 cm Ⅷ 8 cm 5 cm 30 º ر 8 cm 5 cm Ⅱ 30 º ر 8 cm 5 cm 2. 如图 ， AB = DB ， BC = BE ， 欲证 △ ABE ≌ △ DBC ， 则需要增加的条件是 ( ) A. ∠ A ＝ ∠ D B. ∠ E ＝ ∠ C C. ∠ A = ∠ C D. ∠ ABD ＝ ∠ EBC   D 3. 如图，点 E 、 F 在 AC 上， AD // BC ， AD = CB ， AE = CF . 求证 ： △ AFD ≌ △ CEB . F A B D C E 证明 ： ∵ AD // BC ， ∴ ∠ A =∠ C ， ∵ AE = CF ， 在 △ AFD 和△ CEB 中 ， AD = CB ∠ A =∠ C AF = CE ∴ △ AFD ≌ △ CEB （ SAS ） . ∴ AE+EF=CF+EF ， 即 AF = CE . ( 已知 ）， ( 已证 ）， ( 已证 ）， 4. 已知：如图 ， AB = AC , AD 是△ ABC 的角平分线， 求证： BD = CD . 证明： ∵AD 是△ ABC 的角平分线， ∴ ∠ BAD =∠ CAD ， 在 △ ABD 和△ ACD 中 ， AB = AC ∠ BAD =∠ CAD AD = AD ∴ △ ABD ≌ △ ACD （ SAS ） . ( 已知 ）， ( 已证 ）， ( 已证 ）， ∴ BD = CD . 已知：如图 ， AB=AC, BD=CD ， 求证： ∠ BAD= ∠ CAD. 变式 1 证明： ∴ ∠ BAD =∠ CAD ， 在 △ ABD 和△ ACD 中 ， ∴ △ ABD ≌ △ ACD （ SSS ） . AB = AC BD = CD AD = AD ( 已知 ）， ( 公共边）， ( 已知 ）， 已知：如图 ， AB=AC, BD=CD ， E 为 AD 上一点 ， 求证： BE = CE . 变式 2 证明： ∴ ∠ BAD =∠ CAD ， 在 △ ABD 和△ ACD 中 ， AB = AC BD = CD AD = AD ( 已知 ）， ( 公共边）， ( 已知 ）， ∴ BE = CE . 在 △ ABE 和△ ACE 中 ， AB = AC ∠ BAD =∠ CAD AE = AE ( 已知 ）， ( 公共边）， ( 已证 ）， ∴ △ ABD ≌ △ ACD （ S S S ） . ∴ △ ABE ≌ △ ACE （ S A S ） . 5. 如图，已知CA=CB,AD=BD, M，N分别是CA，CB的中点，求证：DM=DN . 在 △ABD 与 △CBD 中 证明 : CA=CB ( 已知） AD=BD （已知） CD=CD （公共边） ∴△ACD ≌ △BCD （ SSS ） 能力提升 连接 CD ，如图所示； ∴ ∠A=∠B 又 ∵ M，N分别是CA，CB的中点， ∴ AM=BN 在 △AMD 与 △BND 中 AM=BN ( 已证） ∠ A= ∠ B （已证） AD=BD （已知） ∴△AMD ≌ △ B ND （ SAS ） ∴ DM=DN. 课堂小结 边角边 内容 有两边及夹角对应相等的两个三角形全等（简写成 “ SAS ”) 应用 为证明线段和角相等提供了新的证法 注意 1. 已知两边，必须找“夹角” 2. 已知一角和这角的一夹边，必须找这角的另一夹边