最新冀教版初中数学八年级上册《16-3角的平分线》检测试卷 (1)

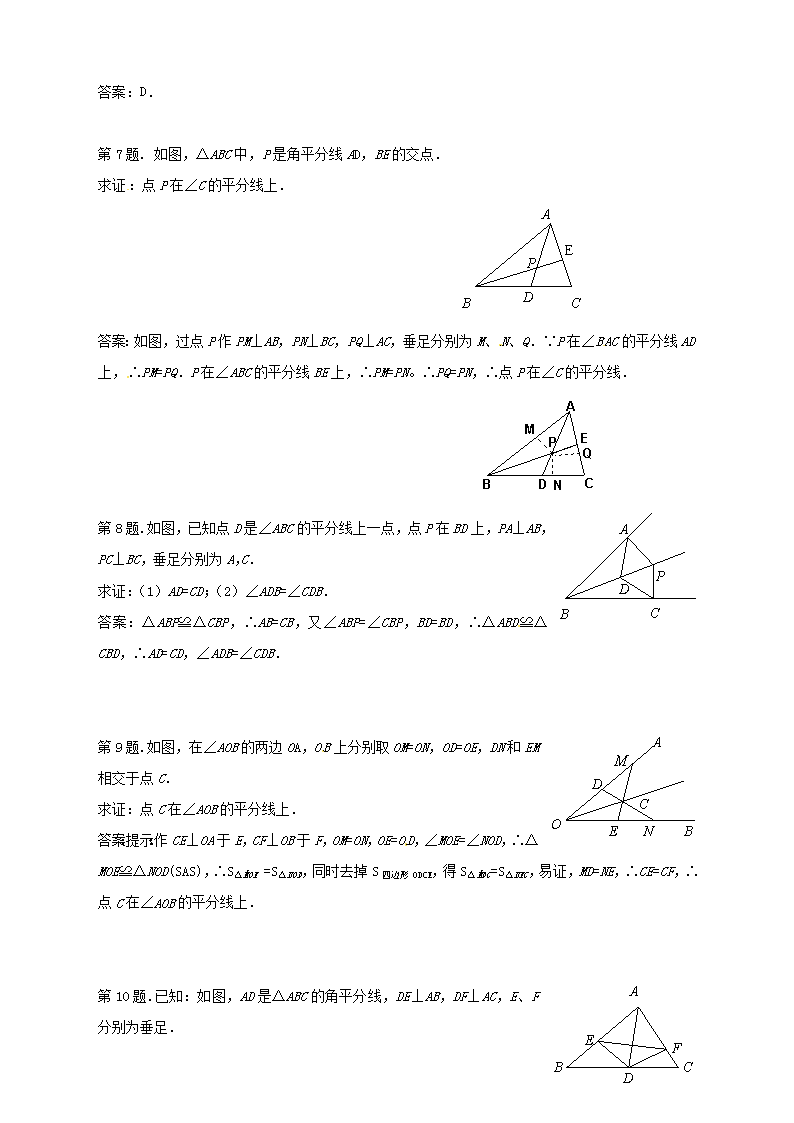
最新冀教版初中数学八年级上册《16-3角的平分线》检测试卷 (1)

24.8 角平分线的性质及其逆定理 第 1 题.如图，△ABC 中，AD 为∠BAC 的平分线，DE⊥AB，DF⊥AC，E、F 为垂 足，在以下结论中：①△ADE≌△ADF；②△BDE≌△CDF；③△ABD≌△ACD；④ AE=AF；⑤BE=CF；⑥BD=CD．其中正确结论的个数是（ ） A．1 B．2 C．3 D．4 答案：B． 第 2 题.如图，Rt△ABC 中，∠C=90º，BD 是角平分线，DE⊥AB，垂足为E，BC=6， CD=3，AE=4，则 DE=_______，AD=_______，△ABC 的周长是_______． 答案：3，5，24 第 3 题.用三角尺画角平分线：如图，∠AOB 是一个任意角，在边 OA，OB 上分别取 OM=ON，再分别过 M、N 作 OA，OB 的垂线，交点为 P，画射线 OP， 则这条射线即为角平分线．请解释这种做法的道理．你还能举出哪些作角 平分线的方法，并说明这种做法的道理． 答案：提示：OM=ON，OP=OP，∴Rt△OMP≌Rt△ONP(HL)，∴∠MOP=∠NOP， ∴射线 OP 是∠AOB 的平分线． 第 4 题. 求证：三角形的三条角平分线相交于一点． 答案：提示：画出图形，写出已知、求证，证明两条角平分线的交点到第三个角的两边的距离相等． 第 5 题.如图，三条公路围成的一个三角形区域，要在这个区域中建一 个加油站，使它到三条公路的距离都相等，加油站应建在什么位置？请 用尺规作图，找出建造加油站的位置． 答案：提示：作两个角的平分线，交点即为建加油站的位置． 第 6 题.如图，△ABC 中，∠C=90º，BD 平分∠ABC 交 AC 于 D，DE 是 AB 的垂 直平分线，DE= 2 1 BD，且 DE=1.5cm，则 AC 等于（ ） A．3cm B．7.5cm C．6cm D．4.5cm 答案：D． A B CD E F A BC D E B C D E A 第 7 题. 如图，△ABC 中，P 是角平分线 AD，BE 的交点． 求证：点 P 在∠C 的平分线上． 答案：如图，过点 P 作 PM⊥AB，PN⊥BC，PQ⊥AC，垂足分别为 M、 N、Q．∵P 在∠BAC 的平分线 AD 上，∴PM=PQ．P 在∠ABC 的平分线 BE 上，∴PM=PN。∴PQ=PN，∴点 P 在∠C 的平分线． 第 8 题.如图，已知点 D 是∠ABC 的平分线上一点，点 P 在 BD 上，PA⊥AB， PC⊥BC，垂足分别为 A，C． 求证：（1）AD=CD；（2）∠ADB=∠CDB． 答案：△ABP≌△CBP，∴AB=CB，又∠ABP=∠CBP，BD=BD，∴△ABD≌△CBD， ∴AD=CD，∠ADB=∠CDB． 第 9 题.如图，在∠AOB 的两边 OA，OB 上分别取 OM=ON，OD=OE，DN 和 EM 相交于点 C． 求证：点 C 在∠AOB 的平分线上． 答案：提示：作 CE⊥OA 于 E，CF⊥OB 于 F，OM=ON，OE=OD，∠MOE=∠NOD， ∴△MOE≌△NOD(SAS)，∴S△MOE =S△NOD，同时去掉 S 四边形 ODCE，得 S△MDC=S△NEC，易证，MD=NE，∴CE=CF， ∴点 C 在∠AOB 的平分线上． 第 10 题.已知：如图，AD 是△ABC 的角平分线，DE⊥AB，DF⊥AC，E、F 分别为垂足． 求证：AD 垂直平分 EF． A B CD E P A B C P D EM N Q A B C D P A B D C EO M N A B CD E F 答案：提示：由角平分线的性质定理，可得 DE=DF，进而求得∠DEF=∠DFE，∠AEF=∠AFE，所以 AE=AF， 所以 AD 垂直平分 EF． 第 11 题.如图，已知△ABC 中，∠C=90º，∠BAC=2∠B，D 是 BC 上一点， DE⊥AB 于 E，DE=DC． 求证：AD=BD． 答案：提示：DE=DC，AD=AD，∴Rt△ADE≌Rt△ADC，∴∠EAD=∠DAC= 1 2 ∠BAC，又∠B= 1 2 ∠BAC，∴∠EAD=∠B，∴AD=BD． A B D C E