- 2021-10-27 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
等腰三角形性质教案
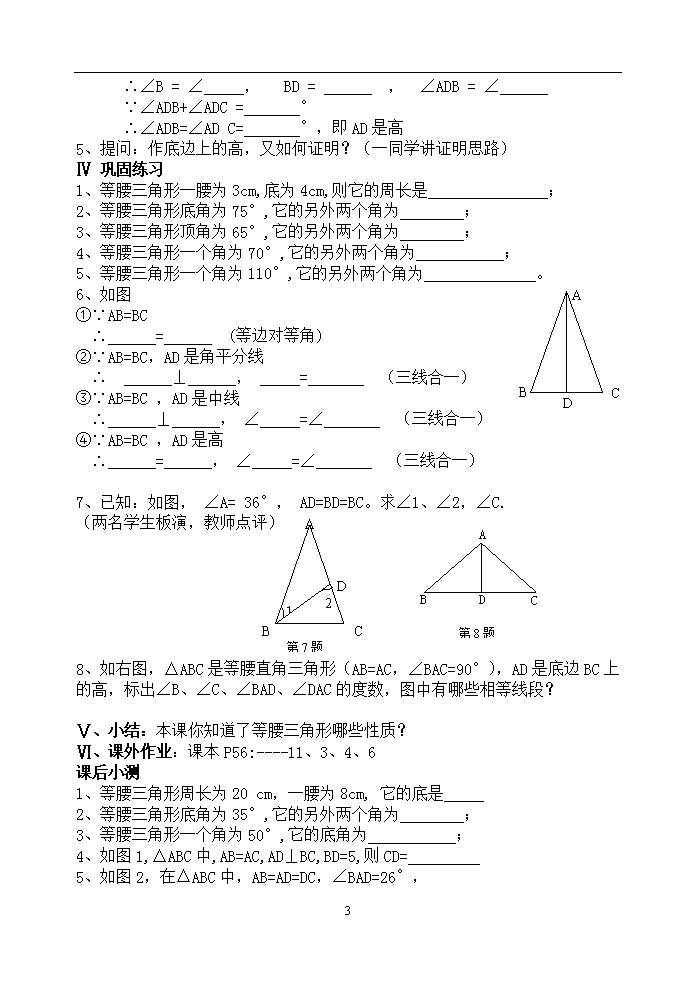
等腰三角形 教学目标 1.知识与技能 理解并掌握等腰三角形的定义,探索等腰三角形的性质;能够用等腰三角形的性质解决相应的数学问题. 2.过程与方法 在探索等腰三角形的性质的过程中体会知识间的关系,感受数学与生活的联系. 3.情感、态度与价值观 培养学生分析解决问题的能力,使学生养成良好的学习习惯. 教学重点: 1.等腰三角形的概念及性质. 2.等腰三角形性质的应用. 教学难点:等腰三角形三线合一的性质的理解及其应用. 教学方法:创设情境-主体探究-合作交流-应用提高. 教具准备 师:多媒体课件、投影仪; 生:硬纸、剪刀 教学过程 Ⅰ.创设情境 前面的学习中,认识了轴对称图形,探究了轴对称的性质.这节课从轴对称的角度来认识一些我们熟悉的几何图形.来研究:①三角形是轴对称图形吗?②什么样的三角形是轴对称图形? Ⅱ.自主探究(分组活动) 活动A:把一张长方形纸对折,在折痕处剪去一个直角,再把它展开,得到一个三角形,此三角形有何特点? 活动B: 画一画,量一量 (1)作一条直线L,在L上取点A,在L外取点B,作出点B关于直线L的对称点C,连结AB、BC、CA,则可得到一个△ABC. (2)用刻度尺量一量三角形的两边AB、AC,看它们的长度有何关系? Ⅲ。互动探究 探究1:实践观察,认识等腰三角形(结合课件) 以上活动所得三角形的两边相等吗? 此三角形称为 。 4 小结:填出等腰三角形各部分名称 探究2:等腰三角形的性质 问题1.等腰三角形是轴对称图形吗?请找出它的对称轴. 问题2.折叠或量,看看等腰三角形的两底角有什么关系? 问题3.顶角的平分线所在的直线是等腰三角形的对称轴吗? 问题4.底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在的直线呢? 1、学生通过刚才自主探究,大胆猜想以上问题的结果。 2、教师用几何画板直观演示并引导学生观察等腰三角形的性质。(对称性,等边对等角,“三线合一”) A B C D E F A B C D(E、F) 使AB=AC 小结:等腰三角形的性质: (1)等腰三角形的两个底角 ,简写成“ ”; (2)等腰三角形的 , 、 互相重合(通常称作“三线合一”)。 3、你能证明以上性质吗? 问题(1)性质1(等腰三角形的两个底角相等)的条件和结论分别是什么? (2)怎样用数学符号表达条件和结论? 已知:如图 已知△ABC中,AB=AC,AD是底边上的中线. 求证: (1)∠B=∠C; (2)AD平分∠A,AD⊥BC. (3)如何证明? (4)受上述启发,能证明性质2吗? (阅读课本P50页例1以前的内容) A B C D 请以“作顶角的角平分线”为辅助线,证明以上性质。(A 组同学完成以下填空,B组独立证明)教师巡视辅导点评。 证明:作∠BAC的平分线AD ∴∠ =∠ 在△ABD与△ACD中 = (已知) ∠ =∠ AD = AD (公共边) ∴△ABD≌△ACD ( ) 4 ∴∠B = ∠ , BD = , ∠ADB = ∠ ∵∠ADB+∠ADC = ° ∴∠ADB=∠AD C= °,即AD是高 5、提问:作底边上的高,又如何证明?(一同学讲证明思路) Ⅳ 巩固练习 1、等腰三角形一腰为3cm,底为4cm,则它的周长是 ; 2、等腰三角形底角为75°,它的另外两个角为 ; 3、等腰三角形顶角为65°,它的另外两个角为 ; 4、等腰三角形一个角为70°,它的另外两个角为 ; A B C D 5、等腰三角形一个角为110°,它的另外两个角为 。 6、如图 ①∵AB=BC ∴ = (等边对等角) ②∵AB=BC,AD是角平分线 ∴ ⊥ , = (三线合一) ③∵AB=BC ,AD是中线 ∴ ⊥ , ∠ =∠ (三线合一) ④∵AB=BC ,AD是高 ∴ = , ∠ =∠ (三线合一) C B A D 2 1 第7题 第8题 7、已知:如图, ∠A= 36°, AD=BD=BC。求∠1、∠2,∠C. (两名学生板演,教师点评) 8、如右图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、∠C、∠BAD、∠DAC的度数,图中有哪些相等线段? Ⅴ、小结:本课你知道了等腰三角形哪些性质? Ⅵ、课外作业:课本P56:----11、3、4、6 课后小测 1、等腰三角形周长为20 cm,一腰为8cm, 它的底是 2、等腰三角形底角为35°,它的另外两个角为 ; 3、等腰三角形一个角为50°,它的底角为 ; 4、如图1,△ABC中,AB=AC,AD⊥BC,BD=5,则CD= 5、如图2,在△ABC中,AB=AD=DC,∠BAD=26°, 4 图1 图2 求∠B和∠C的度数。 板书设计 等腰三角形性质(一) 一、认识等腰三角形 二、等腰三角形的性质 三、等腰三角形的性质的证明 四、等腰三角形的性质的应用 4查看更多