变化的鱼（2）教案

变化的鱼（2）教案

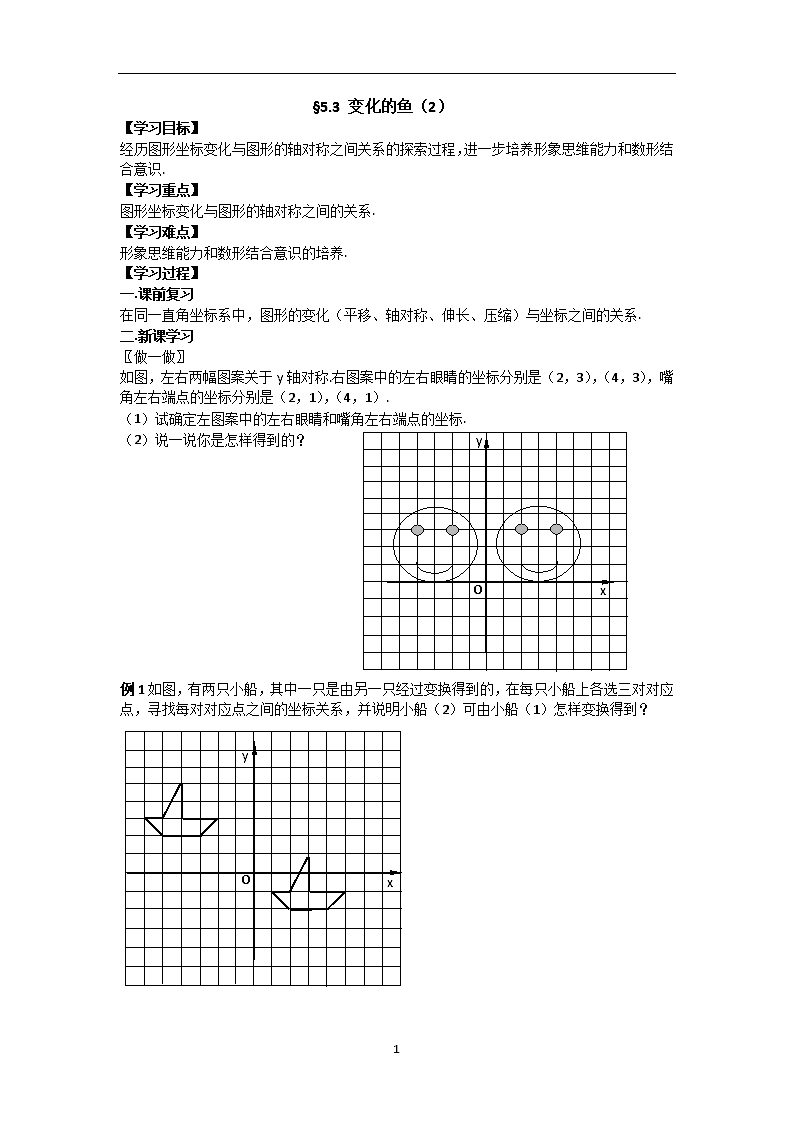
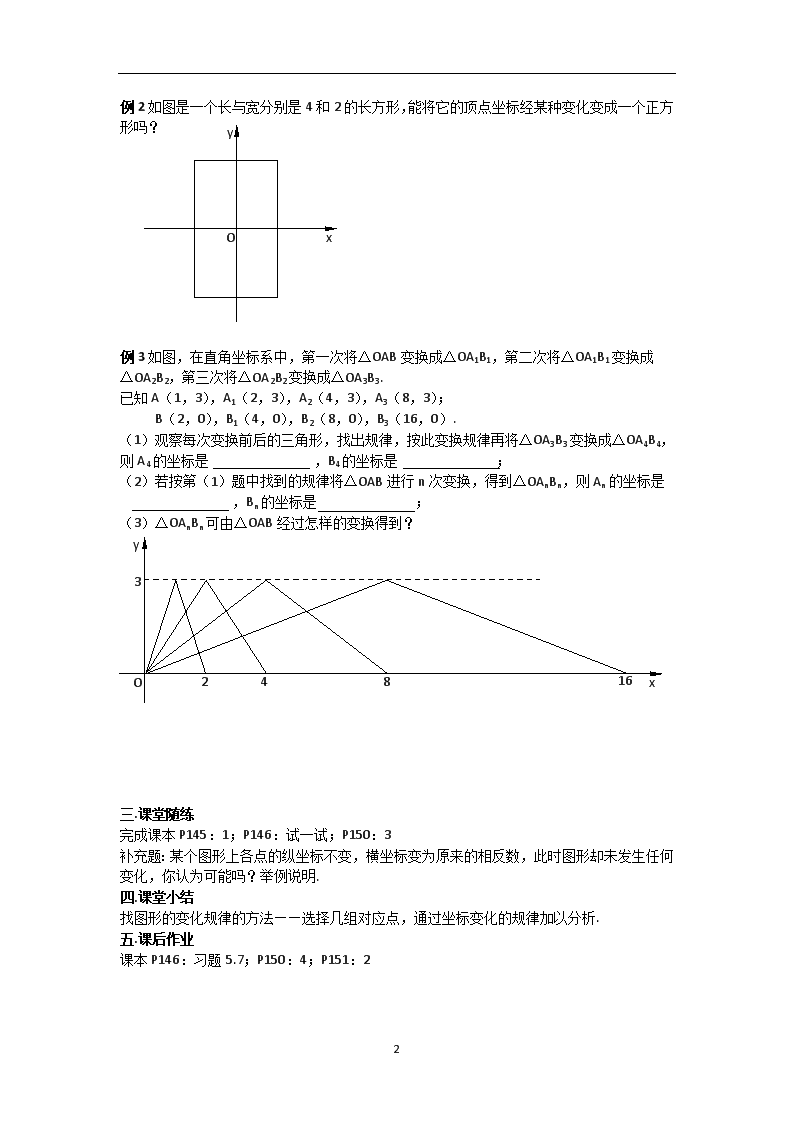
‎ ‎ ‎§5.3 变化的鱼（2）‎ ‎【学习目标】‎ 经历图形坐标变化与图形的轴对称之间关系的探索过程，进一步培养形象思维能力和数形结合意识.‎ ‎【学习重点】‎ 图形坐标变化与图形的轴对称之间的关系.‎ ‎【学习难点】‎ 形象思维能力和数形结合意识的培养.‎ ‎【学习过程】‎ 一.课前复习 在同一直角坐标系中，图形的变化（平移、轴对称、伸长、压缩）与坐标之间的关系.‎ 二.新课学习 ‎〖做一做〗‎ 如图，左右两幅图案关于y轴对称.右图案中的左右眼睛的坐标分别是（2，3），（4，3），嘴角左右端点的坐标分别是（2，1），（4，1）.‎ x y O ‎（1）试确定左图案中的左右眼睛和嘴角左右端点的坐标.‎ ‎（2）说一说你是怎样得到的？‎ 例1如图，有两只小船，其中一只是由另一只经过变换得到的，在每只小船上各选三对对应点，寻找每对对应点之间的坐标关系，并说明小船（2）可由小船（1）怎样变换得到？‎ x y O 2‎ ‎ ‎ x y O 例2如图是一个长与宽分别是4和2的长方形，能将它的顶点坐标经某种变化变成一个正方形吗？‎ 例3如图，在直角坐标系中，第一次将ΔOAB变换成ΔOA1B1，第二次将ΔOA1B1变换成 ΔOA2B2，第三次将ΔOA2B2变换成ΔOA3B3.‎ 已知A（1，3），A1（2，3），A2（4，3），A3（8，3）；‎ ‎ B（2，0），B1（4，0），B2（8，0），B3（16，0）.‎ ‎（1）观察每次变换前后的三角形，找出规律，按此变换规律再将ΔOA3B3变换成ΔOA4B4，‎ 则A4的坐标是 ，B4的坐标是 ；‎ ‎（2）若按第（1）题中找到的规律将ΔOAB进行n次变换，得到ΔOAnBn，则An的坐标是 ‎ ，Bn的坐标是 ；‎ x y O ‎2‎ ‎4‎ ‎8‎ ‎16‎ ‎3‎ ‎（3）ΔOAnBn可由ΔOAB经过怎样的变换得到？‎ 三.课堂随练 完成课本P145：1；P146：试一试；P150：3‎ 补充题：某个图形上各点的纵坐标不变，横坐标变为原来的相反数，此时图形却未发生任何变化，你认为可能吗？举例说明.‎ 四.课堂小结 找图形的变化规律的方法——选择几组对应点，通过坐标变化的规律加以分析.‎ 五.课后作业 课本P146：习题5.7；P150：4；P151：2‎ 2‎