八上时 一次函数与二元一次方程组

八上时 一次函数与二元一次方程组

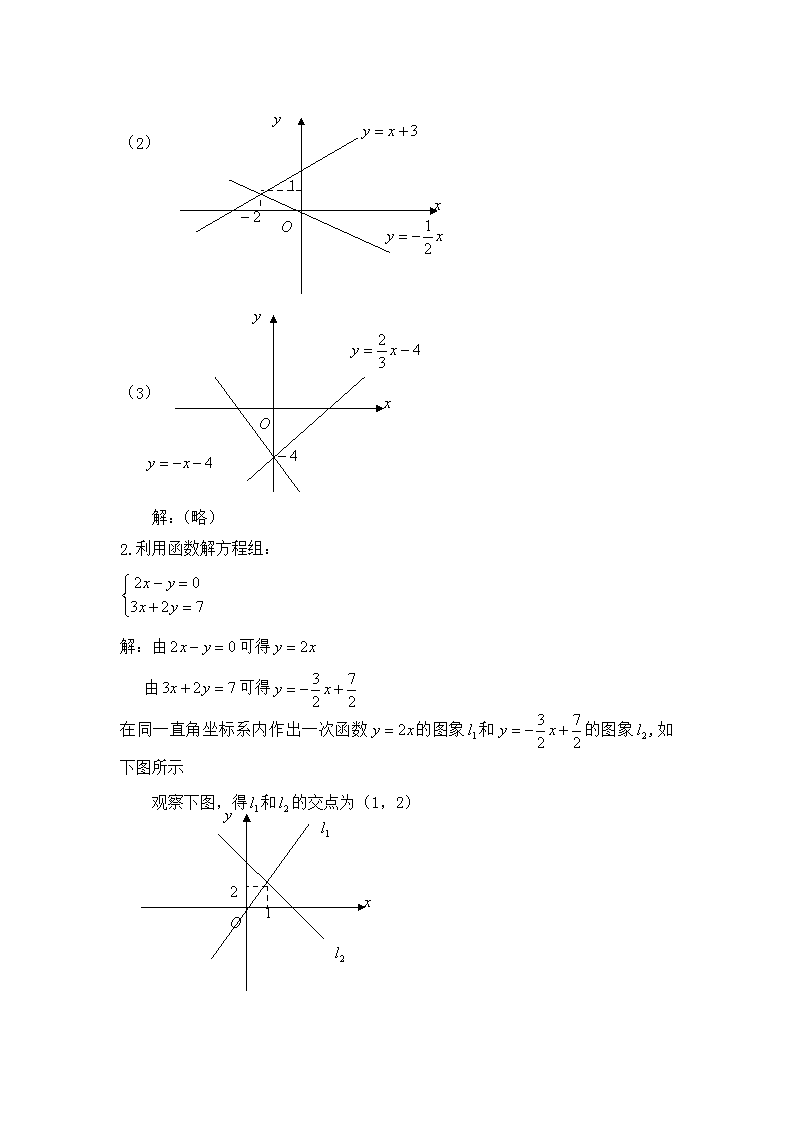
‎11.3.3‎‎ 一次函数与二元一次方程(组)‎ 教学目标 ‎1. 理解一次函数与二元一次方程组的关系，会用图象法解二元一次方程组；‎ ‎2. 学习用函数的观点看待方程组的方法，进一步感受数形结合的思想方法；‎ ‎3. 历图象法解方程组的探究过程，学习用联系的观点看待数学问题的辩证思想 教学重点 对应关系的理解及实际问题的探究建模 教学难点 二元一次方程组的解与两直线交点坐标之间的对应关系的理解 教学过程 I 提出问题，复习引新 我们已经学会了如何求一个二元一次方程组的解的方法，比如可以用代人法，也可以用加减法．我们如何用函数的观点去看待方程组的解呢? ‎ 首先，任何一个方程组都可以看成是两个一次函数的组合．比如 ‎ ①‎ 对于①，根据方程组解的意义和函数的观点，就是求当x取什么数值时，两个—次函数的y值相等?它反映在图象上，就是求直线和直线的交点坐标.‎ 七年级下学期学习二元一次方程组时，有一个数学活动，就谈到了，求方程组的解就是求两条直线的交点坐标．‎ ‎ II 例题与练习 ‎1．根据下列图象，你能说出哪些方程组的解?这些解是什么?‎ ‎（1） ‎ ‎（2）‎ ‎（3）‎ 解：（略）‎ ‎2.利用函数解方程组：‎ 解：由可得 由可得 在同一直角坐标系内作出一次函数的图象和的图象,如下图所示 观察下图，得和的交点为（1，2）‎ 所以方程组的解为 ‎3.求直线与直线的交点坐标。你有哪些方法?；与同伴交流，并一起分析各种方法的利弊．‎ ‎ 解法思路l：画出图象找出交点，确定交点坐标近似值．(由于两直线斜率接近，交点的确定，因作图误差可能有较大差别)‎ 解法思路2：由解方程组，得到交点坐标．(把形的问题归结为数的解决，便捷准确)‎ 二元一次方程组的解 III 小结 ‎（1）对应关系 两个一次函数图的交点坐标 ‎(2)图象法解方程组的步骤：‎ ‎①将方程组中各方程化为)的形式；‎ ‎②画出各个一次函数的图象； ‎ ‎③由交点坐标得出方程组的解．‎ 作业 ‎1．P45页习题11．3第5、6、9题． 第46页习题11.3第11题 ‎2．《课堂感悟与探究》‎ ‎3、已知直线与直线的交点横坐标为2，求k的值和交点纵坐标．‎ ‎4．补充题 ‎(1)A、B两地相距100千米，甲、乙两人骑车同时分别从A、B两地相向而行．假设他们都保持匀速行驶,则他们各自离A地的距离s(千米)都是骑车时间t(时)的一次函数．1小时后乙距离A地80千米；2小时后甲距离A地30千米，问经过多长时间两人将相遇? ‎ ‎ (2)求如下图所示的两直线、的交点坐标。(要求结果为精确值).‎