八年级上数学课件八年级上册数学课件《勾股定理的图形验证》 北师大版 (7)_北师大版

八年级上数学课件八年级上册数学课件《勾股定理的图形验证》 北师大版 (7)_北师大版

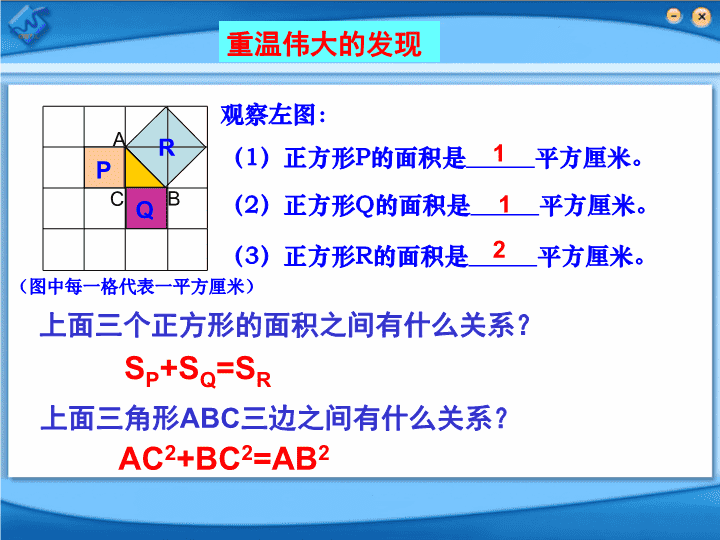
17.1勾股定理（1） 相传2500年前，毕达哥拉斯有一次在朋友家作客时，发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系．我们也来观察右图中的地面图案，看看能发现些什么？重温伟大的发现 （图中每一格代表一平方厘米）观察左图：（1）正方形P的面积是平方厘米。（2）正方形Q的面积是平方厘米。（3）正方形R的面积是平方厘米。121SP+SQ=SRRQPACBAC2+BC2=AB2重温伟大的发现上面三个正方形的面积之间有什么关系？上面三角形ABC三边之间有什么关系？ ABCRQP把R看作是大正方形面积减去四个直角三角形的面积。（图中每一格代表一平方厘米）重温伟大的发现 ABCRQP把R看作是小正方形面积加上四个直角三角形的面积。（图中每一格代表一平方厘米）重温伟大的发现 ABCRQP（图中每一格代表一平方厘米）观察左图：（1）正方形P的面积是平方厘米。（2）正方形Q的面积是平方厘米。（3）正方形R的面积是平方厘米。9方法二1625（1）你能用直角三角形的边长表示上述正方形的面积吗？（2）你能发现直角三角形三边长度之间存在什么关系吗？SQ=AC2,SP=BC2,SR=AB2方法一AC2+BC2=AB2SQ+SP=SR重温伟大的发现 在下图中用三角尺画出两条直角边分别为5cm、12cm的直角三角形，然后用刻度尺量出斜边的长，并验证上述关系对这个直角三角形是否成立。52+122=132重温伟大的发现 勾股定理：直角三角形的两直角边的平方和等于斜边的平方。ABC在ABC中，C=90AC2+BC2=AB2abc（a2+b2=c2）勾股弦在西方又称为毕达哥拉斯定理……勾股定理ABCabc注意：勾股定理的前提条件是直角三角形！！勾股定理背景资料 勾股定理是“人类最伟大的十个科学发现之一”，是初等几何中的一个基本定理。勾股定理的别称有：毕达哥拉斯定理，商高定理，百牛定理，驴桥定理和埃及三角形等。这个定理有十分悠久的历史，几乎所有文明古国（希腊、中国、埃及、巴比伦、印度等）对此定理都有所研究。　　勾股定理在西方被称为毕达哥拉斯定理，相传是古希腊数学家兼哲学家毕达哥拉斯（Pythagoras，公元前572?～公元前497?）于公元前550年首先发现的。中国古代对这一数学定理的发现和应用，远比毕达哥拉斯早得多。中国最早的一部数学著作——《周髀算经》的开头，记载着一段周公向商高请教数学知识的对话。周公与商高的对话则可以确定在公元前1100年左右的西周时期，比毕达哥拉斯要早了五百多年。勾股定理的历史 abc中国最早对勾股定理进行证明的，是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”（左图），用形数结合得到方法，给出了勾股定理的详细证明。赵爽的这个证明可谓别具匠心，极富创新意识。这个图也被后人称为“赵爽弦图”。大正方形的面积可以表示为：所以：化简得：八年级下册勾股定理的证明2002年在北京召开的国际数学家大会（ICM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就. aaabbbccc大正方形的面积可以表示为：你能通过下图证明勾股定理吗？abc所以：化简得：八年级下册勾股定理的证明 加菲尔德证法（总统证法）:aabbccs梯形=(a+b)(a+b)=(a2+2ab+b2)=a2+ab+b2s梯形=2×ab+c2=ab+c2∵s梯形=s梯形∴a2+ab+b2=ab+c2∴a2+b2=c2詹姆斯·艾伯拉姆·加菲尔德 (1831～1881） 美国政治家、数学家，美国共和党人，美国第20任总统.他在数学方面的贡献主要是在勾股定理的证明方面的新成就，他也是美国历史上唯一一位数学家出身的总统。勾股定理的证明 前面我们利用数格子的方法得到：即直角三角形两直角边的平方和等于斜边的平方CcbaABA的面积+B的面积=C的面积a2+b2=c2回顾&小结：☞从而探索了直角三角形的三边关系，得到勾股定理： 勾股定理的运用勾股定理的运用:已知直角三角形的任意两条边长，求第三条边长.a2=c2-b2b2=c2-a2c2=a2+b2ACBbac 例1如图，在Rt△ABC中,BC=24,AC=7,求AB的长.B24AC7如果将题目变为：在Rt△ABC中,AB=41,BC=40,求AC的长.24∵Rt△ABC中,∠C是直角∴AC2+BC2=AB2∴勾股定理的运用 勾股定理的运用练习：1.设直角三角形的两条直角边分别为a，b，斜边长为c.(1)已知a=6，c=10，求b.(2)已知a=5，c=12，求c.(3)已知c=25,b=15,求a.ACBbac 勾股定理的运用练习：2.如图，图中所有的三角形都是直角三角形，四边形都是正方形。已知正方形A,B,C,D的边长分别是12，16，9，12.求最大的正方形E的面积。 勾股定理的运用练习：3.在Rt△ABC中，AB=c,BC=a,AC=b,(1)已知∠C=90°,a=3,b=4,则c=______;(2)已知∠B=90°,a=3,b=4,则c=_____;55或ABCACB343454.已知Rt△ABC中，a=3,b=4,则c=_____________; 勾股定理的运用例2.如图，在△ABC中，∠A=45°，AB=+1，求：边BC的长。D练习：如图，在△ABC中，∠ACB=900，CD是高，若AB=13cm，AC=5cm，求CD的长；ABCD 勾股定理的运用例3.△ABC中,周长是24,∠C=90°,且b=6,则三角形的面积是多少?ABCabc解：∵周长是24，且b=6∴a+c=24-6=18设a=x,则c=18-x∵∠C=90°,∴a2+b2=c2∴x2+62=(18-x)2解得：x=8 勾股定理的运用拓展练习：如图（1），已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2（如图（2））；……以此下去，则正方形A4B4C4D4的面积为__________.图（1）A1B1C1D1ABCDD2A2B2C2D1C1B1A1ABCD图（2）