八年级上数学课件八年级上册数学课件《三角形外角定理的证明》 北师大版 (5)_北师大版

八年级上数学课件八年级上册数学课件《三角形外角定理的证明》 北师大版 (5)_北师大版

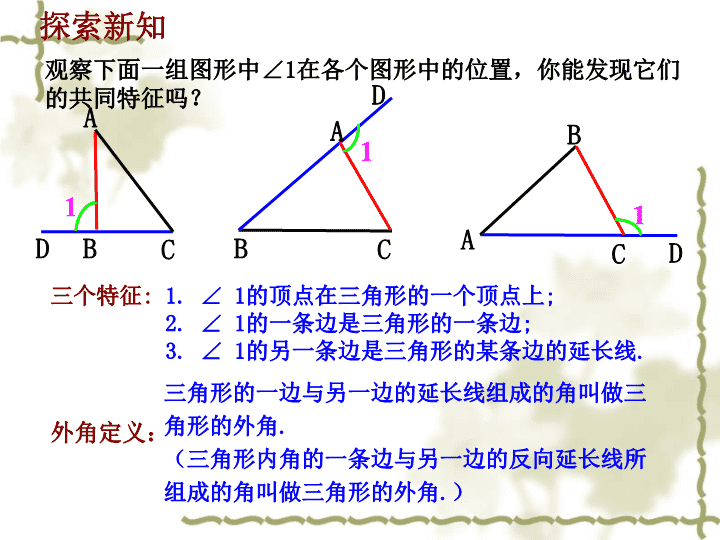
7.5三角形内角和定理（第2课时）北师大版数学八年级上册第七章平行线的证明 三角形内角和定理复习引入自主学习 观察下面一组图形中∠1在各个图形中的位置，你能发现它们的共同特征吗？BCA1DACB1DACB1D外角定义：三角形的一边与另一边的延长线组成的角叫做三角形的外角.（三角形内角的一条边与另一边的反向延长线所组成的角叫做三角形的外角.）三个特征:1.∠1的顶点在三角形的一个顶点上;2.∠1的一条边是三角形的一条边;3.∠1的另一条边是三角形的某条边的延长线.探索新知 大家一起画一画想一想:1、每一个三角形有几个外角？2、每一个顶点处相对应的外角有几个？3、每一个顶点处的外角有什么关系？画一个三角形，再画出它所有的外角. ABDEFC外角ABDEFC外角 124三角形的外角与三角形的内角之间有怎样的数量关系?外角A3BCD相邻内角不相邻内角思考1.相邻的内角：2.不相邻的两内角： 三角形的外角与内角的关系：如图△ABC中，则∠ACB+∠ACD＝？ABCD？？结论：三角形的外角与它相邻的内角互为邻补角即三角形的外角与它相邻内角的和为180° ABC△ABC的外角∠ACD与它不相邻的内角∠A、∠B有怎样的关系？D∠ACD=∠A+∠B能证明这个结论吗？ ABCD证明：△ABC中，∵∠A+∠B+∠ACB=180°（三角形内角和定理）∠ACB+∠ACD=180°（平角定义）∴∠ACD=∠A+∠B（等量代换）∠ACD=∠A+∠B DACB∵∠ACD=∠A+∠B∴∠ACD﹥∠A∠ACD﹥∠B三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系? 三角形内角和定理的推论:推论1:三角形的一个外角等于与它不相邻的两个内角的和.∠B+∠C=∠CAD推论2:三角形的一个外角大于任何一个与它不相邻的内角.∠CAD>∠B，∠CAD>∠CABCD在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.推论可以当作定理使用. 3、三角形的一个外角大于任何一个与它不相邻的内角。2、三角形的一个外角等于与它不相邻的两个内角的和；1、三角形的一个外角与它相邻的内角互补；三角形的外角与内角的关系： 160°110°课堂练习：1、求下列各图中∠1的度数50°45°135°120°1 160°55°2、求各图中∠1的度数100o60o1 3、判断题1、三角形的一个外角等于两个内角的和.2、三角形的一个外角等于与它不相邻的两个内角的和.5、三角形的一个内角小于任何一个与它不相邻的外角.3、三角形的一个外角大于任何一个内角.4、三角形的一个外角大于任何一个与它不相邻的内角.×√×√√ 证明：∵∠EAC=∠B+∠C（三角形的一个外角等于和它不相邻的两个内角的和）∠B=∠C（已知）∴∠C=1/2∠EAC（等式的性质）∵AD平分∠EAC（已知）∴∠DAC=1/2∠EAC（角平分线的定义）∴∠DAC=∠C（等量代换）∴AD∥BC（内错角相等，两直线平行）例题解析：例2:已知：如图,在三角形ABC中,AD平分外角∠EAC,∠B=∠C.求证：AD∥BCABCDE对于此题还有其它的证明方法吗？ 试比较∠1、∠A的大小关系？你能比较∠2、∠A的关系么？试试看。2PABCD1巩固拓展 例3:已知:如图,P是△ABC内一点,连接PB，PC.求证:∠BPC＞∠A.ABDPC证明:延长BP，交AC于点D.∵∠BPC是△PCD的一个外角（外角的定义）∴∠BPC＞∠PDC.（三角形的一个外角大于任何一个和它不相邻的内角）∵∠PDC是△ABD的一个外角（外角的定义）∴∠PDC＞∠A.（三角形的一个外角大于任何一个和它不相邻的内角）∴∠BPC＞∠A. 321ABC564已知：如图，∠1、∠2、∠3是△ABC的三个外角，它们的和是多少度？∠1+∠2+∠3=360°结论：三角形的外角和等于360°通常把一个三角形每一个顶点处的一个外角的和叫做三角形的外角和。提高升华： 跟踪练习1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是三角形2.如图1,若∠A=32°,∠B=45°,∠C=38°,则∠DFE＝°FEDCBA115钝角3.如图2，∠1=_______.120°140°80°14.已知等腰三角形的一个外角为150°,则它的底角为_____.30或75°5.如图3，∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.120°DCBA图1图2图3 6.(1)如图(甲)，在五角星图形中，求∠A+∠B+∠C+∠D+∠E的度数.(2)把图（乙）、（丙）叫蜕化的五角星，问它们的五角之和与五角星图形的五角之和仍相等吗？为什么？AEABCDAE(甲)EBCDDCB(乙)(丙)分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解. 7.如图，把△ACB沿DE折叠，当点A落在四边形BCED内部时，∠DAE与∠1,∠2之间有一种数量关系保持不变，这一规律是（）A.∠A=∠1+∠2B.2∠A=∠1+∠2C.3∠A=2∠1+∠2D.3∠A=2（∠1+∠2）BDAACE12B 今天的收获课堂小结：1三角形的外角性质：三角形的一个外角等于与它不相邻的两个内角的和；三角形的一个外角大于任何一个与它不相邻的内角。2三角形的内角和等于180˚三角形的外角和等于360˚3在求角的度数时，常可利用三角形的内角和及外角的性质来找数量关系；涉及图形时，可先把已知条件尽可能的在图中标出来，有助于直观分析题意。4不等关系的证明思路