浙教版八年级上册数学同步课件-第2章-2 等腰三角形的性质定理

浙教版八年级上册数学同步课件-第2章-2 等腰三角形的性质定理

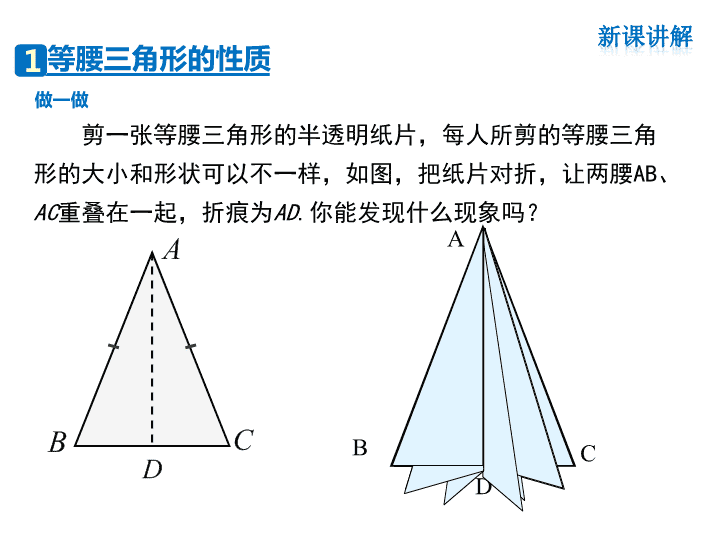
第2章特殊三角形2.3等腰三角形的性质定理 有两条边相等的三角形叫做等腰三角形.等腰三角形中，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.ACB腰腰底边顶角底角底角复习引入新课引入 剪一张等腰三角形的半透明纸片，每人所剪的等腰三角形的大小和形状可以不一样，如图，把纸片对折，让两腰AB、AC重叠在一起，折痕为AD.你能发现什么现象吗？做一做DABC等腰三角形的性质新课讲解1 1.等腰三角形是轴对称图形.我们可以得出结论：ACBD折痕AD所在直线是等腰三角形的对称轴.你还有新的发现吗？∠B、∠C是等腰三角形的.底角∠B＝∠C所以我们可以描述为:等腰三角形的两个底角相等.2.探究归纳新课讲解 等腰三角形的性质：等腰三角形的两个底角相等（简写成“等边对等角”）.已知：如图，△ABC中，AB=AC,求证：∠B=∠C.证明：作顶角∠BAC的平分线AD.在△ABD与△ACD中，AB＝AC（已知），∠1＝∠2（已证），AD＝AD（公共边），∴△ABD≌△ACD（S.A.S.），∴∠B＝∠C.ABCD((12分析：由上述操作可以得到启发，即添加等腰三角形的顶角平分线AD，然后证明△ABD≌△ACD.从这里你还可以得到什么结论?新课讲解 想一想：刚才的证明除了能得到∠B＝∠C，你还能发现什么?重合的线段重合的角ABDCAB＝ACBD＝CDAD＝AD∠B＝∠C∠BAD＝∠CAD∠ADB＝∠ADC=90°新课讲解 性质等腰三角形底边上的高、中线及顶角的平分线，互相重合（简称“三线合一”）.ABCD((12填一填:根据等腰三角形性质完成下列填空.在△ABC中，AB=AC时，（1）∵AD是底边上的高，∴∠_____=∠_____，____=____.(2)∵AD是中线，∴____⊥____，∠_____=∠_____.(3)∵AD是角平分线，∴____⊥____，_____=_____.122BDCDADBCBD1BCADCD新课讲解 例1已知：在△ABC中，AB=AC，∠B=80°，求∠C和∠A的大小.解：典例精析新课讲解 例2在△ABC中，AB=AC，D是BC边上的中点，∠B=30°.求：（1）∠ADC的大小；（2）∠1的大小.ADC12(2)∵∠1+∠B+∠ADB=180°（三角形内角和等于180°），∠B=30°（已知），∴∠1=180°-∠B-∠ADB=180°-30°-90°=60°.∴AD⊥BC(等腰三角形“三线合一”).∴∠ADC=∠ADB=90°(垂直的定义).解：(1)∵AB=AC，BD=DC（已知），B新课讲解 因为等边三角形是特殊的等腰三角形，由等腰三角形等边对等角的性质得到，∠B＝∠C，同理可得∠A＝∠B,所以∠A＝∠B＝∠C，又由∠A＋∠B＋∠C＝180°，从而推出∠A＝∠B＝∠C＝60°.也就是说：等边三角形的各个角都相等，并且每一个角都等于60°.三条边都相等的三角形是等边三角形，它也是轴对称图形，那么等边三角形的每个角的度数是多少呢？它有几条对称轴？ACB等边三角形的三条边都相等，三个角都相等，也称为正三角形.三条对称轴等边三角形的性质新课讲解2 ABCD例3如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.（1）找出图中所有相等的角；（2）指出图中有几个等腰三角形？∠A=∠ABD,∠C=∠BDC=∠ABC.△ABC,△ABD,△BCD.新课讲解典例精析 ABCDx⌒2x⌒2x⌒⌒2x（3）观察∠BDC与∠A、∠ABD的关系，∠ABC、∠C呢？∠BDC=∠A+∠ABD=2∠A=2∠ABD,∠ABC=∠BDC=2∠A,∠C=∠BDC=2∠A.（4）设∠A=x,请把△ABC的内角和用含x的式子表示出来.∵∠A+∠ABC+∠C=180°，∴x+2x+2x=180°.新课讲解 ABCD解：∵AB=AC，BD=BC=AD，∴∠ABC=∠C=∠BDC，∠A=∠ABD.设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x,于是在△ABC中，有∠A+∠ABC+∠C=x+2x+2x=180°，解得x=36°.在△ABC中，∠A=36°，∠ABC=∠C=72°.x⌒2x⌒2x⌒⌒2x新课讲解 1.如图，在下列等腰三角形中，分别求出它们的底角的度数.ABC120°ABC36°∠B=∠C=72°∠B=∠C=30°随堂即练 2.(1)等腰三角形一个底角为75°,它的另外两个角为；(2)等腰三角形一个角为36°,它的另外两个角为____________________；(3)等腰三角形一个角为120°,它的另外两个角为.75°,30°72°,72°或36°,108°30°，30°结论:在等腰三角形中,注意对角的分类讨论.①顶角+2×底角=180°②顶角=180°－2×底角③底角=（180°－顶角）÷2④0°＜顶角＜180°⑤0°＜底角＜90°随堂即练 等腰三角形的性质等边对等角等边三角形注意是指同一个三角形中注意：顶角的平分线、底边上的高和中线才有这一性质.而腰上高、中线和底角的平分线不具有这一性质三线合一有三条对称轴，每个内角等于60°课堂总结