北师版八年级数学上册-第一章检测题

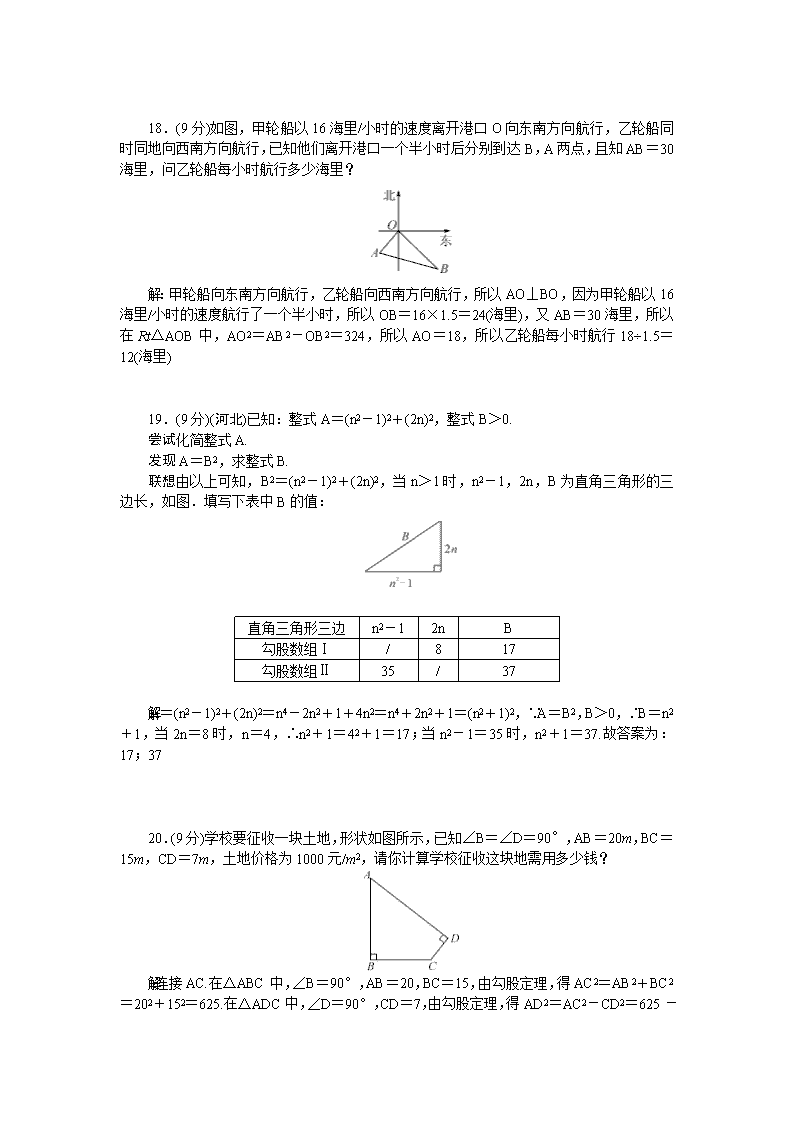
北师版八年级数学上册-第一章检测题

第一章检测题(时间：100分钟满分：120分)一、选择题(每小题3分，共30分)1．(滨州中考)在直角三角形中，若勾为3，股为4，则弦为(A)A．5B．6C．7D．82．如图，在边长为1个单位长度的小正方形组成的网格中，点A，B都是格点，则以AB为边的正方形的面积为(A)A．10B．9C．100D．253．如图，AB⊥CD于点B，△ABD和△BCE都是等腰三角形，如果CD＝17，BE＝5，那么AC的长为(D)A．12B．7C．5D．134．(荆门中考)如图，在△ABC中，AB＝AC，AD是∠BAC的角平分线，已知AB＝5，AD＝3，则BC的长为(C)A．5B．6C．8D．105．在Rt△ABC中，∠C＝90°，AC＝9，BC＝12，则点C到AB的距离为(A)A．B．C．D．6．(咸宁)勾股定理是“人类最伟大的十个科学发现之一”．我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的，他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽．下列图案中是“赵爽弦图”的是(B)7．一架2.5米长的梯子，斜立在一竖直的墙上，这时梯子的底端离墙0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯子底端在水平方向上滑动(B)A．0.9米B．0.8米C．0.5米D．0.4米8．如图，圆柱高8cm，底面圆的半径为cm，一只蚂蚁从点A爬到点B处吃蜂蜜，则要爬行的最短路程是(B)A．20cmB．10cmC．14cmD．无法确定9．如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处，若AB＝3，AD＝4，则ED的长为(A)A．B．3C．1D．10．(宁波)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出(C)A．直角三角形的面积B．最大正方形的面积 C．较小两个正方形重叠部分的面积D．最大正方形与直角三角形的面积和二、填空题(每小题3分，共15分)11．请写出两组你所熟悉的勾股数：__3，4，5__或__6，8，10__等．12．如图，两个正方形的面积分别为9和16，则直角三角形的斜边长为__5__.13．如图，由四个全等的直角三角形拼成的“赵爽弦图”，在Rt△ABF中，∠AFB＝90°，AF＝3，AB＝5，则四边形EFGH的面积是__1__.14．如图有一个棱长为9cm的正方体，一只蜜蜂要沿正方体的表面从顶点A爬到C点(C点在一条棱上，距离顶点B3cm处)，则需爬行的最短路程是__15__cm.15．(郑州期末)如图，这是一个供滑板爱好者使用的U型池的示意图，该U型池可以看成是长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是直径为m的半圆，其边缘AB＝CD＝20m，点E在CD上，CE＝5m，一滑板爱好者从A点滑到E点，则他滑行的最短距离约为__25__m.(边缘部分的厚度忽略不计)三、解答题(共75分)16．(8分)如图，正方形网格中有△ABC，若小方格边长为1，请你根据所学的知识解答下列问题：(1)求△ABC的面积；(2)判断△ABC是什么形状，并说明理由．解：(1)用正方形的面积减去三个小三角形的面积即可求出△ABC的面积．S△ABC＝4×4－1×2×－4×3×－2×4×＝16－1－6－4＝5，所以△ABC的面积为5(2)△ABC是直角三角形．理由如下：因为AB2＝12＋22＝5，AC2＝22＋42＝20，BC2＝32＋42＝25，所以AC2＋AB2＝BC2，所以△ABC是直角三角形17．(9分)如图，AF⊥DE于F，且DF＝15cm，EF＝6cm，AE＝10cm.求正方形ABCD的面积．解：在Rt△AEF中，AF2＝AE2－EF2＝64，在Rt△AFD中，AD2＝AF2＋DF2＝289，所以正方形ABCD的面积是289cm2 18．(9分)如图，甲轮船以16海里/小时的速度离开港口O向东南方向航行，乙轮船同时同地向西南方向航行，已知他们离开港口一个半小时后分别到达B，A两点，且知AB＝30海里，问乙轮船每小时航行多少海里？解：甲轮船向东南方向航行，乙轮船向西南方向航行，所以AO⊥BO，因为甲轮船以16海里/小时的速度航行了一个半小时，所以OB＝16×1.5＝24(海里)，又AB＝30海里，所以在Rt△AOB中，AO2＝AB2－OB2＝324，所以AO＝18，所以乙轮船每小时航行18÷1.5＝12(海里)19．(9分)(河北)已知：整式A＝(n2－1)2＋(2n)2，整式B＞0.尝试化简整式A.发现A＝B2，求整式B.联想由以上可知，B2＝(n2－1)2＋(2n)2，当n＞1时，n2－1，2n，B为直角三角形的三边长，如图．填写下表中B的值：直角三角形三边n2－12nB勾股数组Ⅰ/817勾股数组Ⅱ35/37解：A＝(n2－1)2＋(2n)2＝n4－2n2＋1＋4n2＝n4＋2n2＋1＝(n2＋1)2，∵A＝B2，B＞0，∴B＝n2＋1，当2n＝8时，n＝4，∴n2＋1＝42＋1＝17；当n2－1＝35时，n2＋1＝37.故答案为：17；3720．(9分)学校要征收一块土地，形状如图所示，已知∠B＝∠D＝90°，AB＝20m，BC＝15m，CD＝7m，土地价格为1000元/m2，请你计算学校征收这块地需用多少钱？解：连接AC.在△ABC中，∠B＝90°，AB＝20，BC＝15，由勾股定理，得AC2＝AB2＋BC2＝202＋152＝625.在△ADC中，∠D＝90°，CD＝7，由勾股定理，得AD2＝AC2－CD2 ＝625－72＝576，所以AD＝24.所以四边形ABCD的面积为AB·BC＋CD·AD＝234(m2).234×1000＝234000(元).答：学校征收这块地需要234000元21．(10分)如图，∠AOB＝90°，OA＝45cm，OB＝15cm，一智能机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，智能机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与智能机器人行走的速度相等，那么智能机器人行走的路程BC是多少？解：小球滚动的速度与智能机器人行走的速度相同，时间相同，即BC＝CA，设AC＝x，则OC＝45－x，在Rt△BOC中，OB2＋OC2＝BC2，即152＋(45－x)2＝x2，解得x＝25.所以机器人行走的路程BC是25cm22．(10分)如图，在长方形ABCD中，AB＝8，BC＝6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE＝OD.(1)试证明DG＝EP；(2)求AP的长．解：(1)因为四边形ABCD是长方形，所以∠D＝∠A＝∠C＝90°，AD＝BC＝6，CD＝AB＝8.由折叠的性质可知EP＝AP，BE＝AB＝8，∠E＝∠A＝90°，所以∠E＝∠D.在△ODP和△OEG中，所以△ODP≌△OEG，所以OP＝OG，PD＝GE，所以DO＋OG＝PO＋OE，所以DG＝EP　(2)设AP＝EP＝DG＝x，则GE＝PD＝AD－AP＝6－x，所以CG＝DC－DG＝8－x，BG＝BE－GE＝8－(6－x)＝2＋x.在Rt△CGB中，由勾股定理得BC2＋CG2＝BG2，即62＋(8－x)2＝(x＋2)2，解得x＝4.8，所以AP＝4.823.(11分)如图，在△ABC中，AC＝BC，∠ACB＝90°，点D，E是线段AB上两点．∠DCE＝45°.(1)当CE⊥AB时，点D与点A重合，求证：DE2＝AD2＋BE2； (2)当点D不与点A重合时，求证：DE2＝AD2＋BE2；(3)当点D在BA的延长线上时，(2)中的结论是否成立？画出图形，并说明理由．解：(1)因为CE⊥AB，所以AE＝BE，因为点D与点A重合，所以AD＝0，所以DE2＝AD2＋BE2　(2)如图①，过点A作AF⊥AB，使AF＝BE，连接DF，CF，因为在△ABC中，AC＝BC，∠ACB＝90°，所以∠CAB＝∠B＝45°，所以∠FAC＝45°，所以△CAF≌△CBE(SAS)，所以CF＝CE，∠ACF＝∠BCE，因为∠ACB＝90°，∠DCE＝45°，所以∠ACD＋∠BCE＝∠ACB－∠DCE＝90°－45°＝45°，因为∠ACF＝∠BCE，所以∠ACD＋∠ACF＝45°，即∠DCF＝45°，所以∠DCF＝∠DCE，又因为CD＝CD，所以△CDF≌△CDE(SAS)，所以DF＝DE，因为AD2＋AF2＝DF2，所以AD2＋BE2＝DE2　(3)结论仍然成立．理由：如图②，过点A作AF⊥AB，使AF＝BE，连接DF，CF，因为在△ABC中，AC＝BC，∠ACB＝90°，所以∠CAB＝∠B＝45°，所以∠FAC＝45°，所以△CAF≌△CBE(SAS)，所以CF＝CE，∠ACF＝∠BCE，因为∠BCE＋∠ACE＝90°，所以∠ACF＋∠ACE＝90°，即∠FCE＝90°，因为∠DCE＝45°，所以∠DCF＝45°，所以∠DCF＝∠DCE，又因为CD＝CD，所以△CDF≌△CDE(SAS)，所以DF＝DE，因为AD2＋AF2＝DF2，所以AD2＋BE2＝DE2