八年级上数学课件八年级上册数学课件《三角形内角和定理的证明》 北师大版 (4)_北师大版

八年级上数学课件八年级上册数学课件《三角形内角和定理的证明》 北师大版 (4)_北师大版

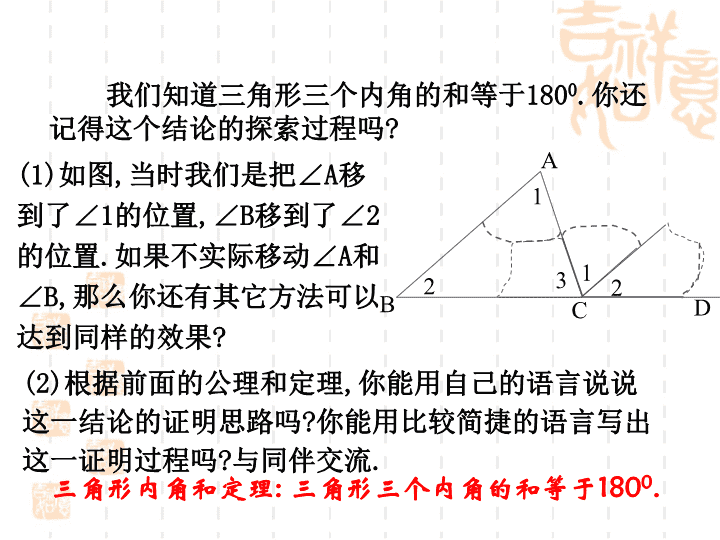
三角形内角和定理的证明 证明命题的一般步骤:(1)理解题意:分清命题的条件(已知),结论(求证);(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(4)分析题意,探索证明思路;(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程; 我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗?112ABD23C(1)如图,当时我们是把∠A移到了∠1的位置,∠B移到了∠2的位置.如果不实际移动∠A和∠B,那么你还有其它方法可以达到同样的效果?(2)根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.三角形内角和定理:三角形三个内角的和等于1800. 已知:如图6-9,△ABC.求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作CE∥AB,则你还有其它方法来证明三角形内角和定理吗?∠1=∠A(两直线平行,内错角相等),∠2=∠B(两直线平行,同位角相等).又∵∠1+∠2+∠3=1800(平角的定义),∴∠A+∠B+∠ACB=1800(等量代换).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABCE213D 在证明三角形内角和定理时,小花的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?请你帮小花把想法化为实际行动.小花的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则ABC∠1=∠B(两直线平行,内错角相等),∠2=∠C(两直线平行,内错角相等),又∵∠1+∠2+∠3=1800(平角的定义),∴∠BAC+∠B+∠C=1800(等量代换).PQ231议一议 根据下面的图形,写出相应的证明.你还能想出其它证法吗?(1)ABCPQRTSN(3)ABCPQRMTSN(2)ABCPQRM试一试 三角形内角和定理三角形内角和定理三角形三个内角的和等于1800.△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:∠A=1800–(∠B+∠C).∠B=1800–(∠A+∠C).∠C=1800–(∠A+∠B).∠A+∠B=1800-∠C.∠B+∠C=1800-∠A.∠A+∠C=1800-∠B.这里的结论,以后可以直接运用.ABC 1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.2.已知:如图在△ABC中，DE∥BC,∠A=600,∠C=700.求证：∠ADE=500.DCBAEABCABC随堂练习 1、如图，已知AD是△ABD和△ACD的公共边.求证：∠BDC=∠BAC+∠B+∠CABCD1234证法一：∵在△ABD中,∠1＝180°－∠B－∠3，在△ADC中,∠2＝180°－∠C－∠4（三角形内角和定理），又∵∠BDC＝360°－∠1－∠2（周角定义）∴∠BDC＝360°－（180°－∠B－∠3）－（180°－∠C－∠4）＝∠B+∠C+∠3+∠4.又∵∠BAC＝∠3+∠4,∴∠BDC＝∠B+∠C+∠BAC（等量代换）练一练 证法二：ABCD12 思考题：如图，已知∠AMN+∠MNF+∠NFC=360°，求证：AB∥CD（用两种方法证明）DFNMBAC