八年级下数学课件《6-3正方形的性质与判定》第2课时_鲁教版

八年级下数学课件《6-3正方形的性质与判定》第2课时_鲁教版

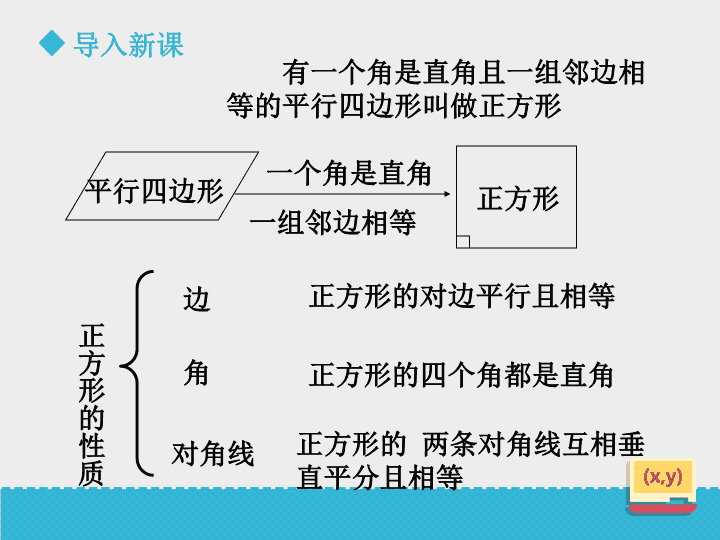
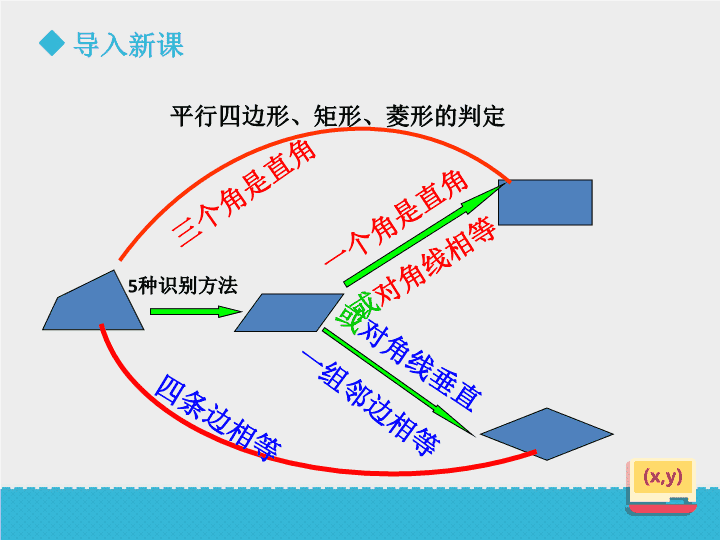
鲁教版初中数学八年级下册第3课第六单元 导入新课一个角是直角有一个角是直角且一组邻边相等的平行四边形叫做正方形正方形平行四边形正方形的两条对角线互相垂直平分且相等正方形的对边平行且相等正方形的四个角都是直角边对角线角正方形的性质一组邻边相等 导入新课平行四边形、矩形、菱形的判定5种识别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直 特殊的平行四边形正方形的判定导入新课 新课学习正方形是特殊的平行四边形，也是特殊的矩形，也是特殊的菱形。要使一个菱形成为正方形需增加的条件是___________（填上一个条件即可）要使一个矩形成为正方形需添加的条件是____________（填上一个条件即可） 新课学习正方形的判定定理定理1：对角线相等的菱形是正方形；定理2：对角线垂直的矩形是正方形；定理3：有一个角是直角的菱形是正方形。 新课学习例2已知：如图，在矩形ABCD中，BE平分∠ABC，CE平分∠DCB，BF∥CE，CF∥BE。求证：四边形BECF是正方形。ABCDEF证明：∵BF∥CE，CF∥BE，∴四边形BECF是平行四边形；∵四边形ABCD是矩形，∴∠ABC=90°，∠DCB=90°；又∵BE平分∠ABC，CE平分∠DCB，∴∠EBC=∠ABC=45°，∠ECB=∠DCB=45°； 新课学习例2已知：如图，在矩形ABCD中，BE平分∠ABC，CE平分∠DCB，BF∥CE，CF∥BE。求证：四边形BECF是正方形。ABCDEF∴∠EBC=∠ECB，∴EB=EC，∴四边形BECF是平行四边形；∴□BECF是菱形，（菱形的定义）在△EBC中，∵∠EBC=45°，∠ECB=45°，∴∠BEC=90°，∴菱形BECF是正方形(有一个直角的菱形是正方形) 新课学习做一做：在正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA的中点，四边形EFGH是正方形吗？为什么？EABCDFHG解：四边形EFGH是正方形，理由如下：连接对角线AC、BD，∵四边形ABCD是正方形，∴AC=BD；又∵点E、F、G、H分别是AB、BC、CD、DA的中点，∴EH=GF=BD，EF=GH=AC； 做一做：在正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA的中点，四边形EFGH是正方形吗？为什么？∴EF=FG=GH=EH，∴四边形EFGH是菱形；又∵△AEH和△DGH是等腰直角三角形，∴∠AHE=∠DHG=45°，∴∠EHG=90°，∴菱形EFGH是正方形(有一个直角的菱形是正方形)新课学习EABCDFHG 新课学习议一议：依次连接平行四边形各边的中点能得到一个什么图形？ABCDEFGH答：得到图形是平行四边形；理由：∵E、F、G、H是各边中点，∴EH是△ABD的中位线，FG是△BCD的中位线，∴EH∥BD，EH=BD，FG∥BD，FG=BD，∴EH∥FG，EH=FG，∴四边形EFGH是平行四边形。 新课学习议一议：依次连接菱形或矩形各边的中点能得到一个什么图形？菱形矩形矩形对角线相等，则新平行四边形四条边相等，则新四边形为菱形。菱形对角线垂直，则新平行四边形邻边垂直，则新四边形为矩形。 新课学习议一议：依次连接四边形各边的中点所得到的新四边形的形状与哪些线段有关系，有怎样的关系？新四边形的形状与原四边形的对角线有关系；新四边形的一组对边与原四边形对应的一条对角线平行，且等于这条对角线的一半；然后根据这两条对角线的关系（相等或垂直）进一步判断新四边形的形状（四条边相等或邻边互相垂直）。 结论总结5种识别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等平行四边形、矩形、菱形、正方形的判定小结 课堂练习1、如图，△ABC中，∠ACB＝90°，CD平分∠ACB，DE⊥BC，DF⊥AC，垂足分别为E、F．求证：四边形CFDE是正方形．证明：∵CD平分∠ACB，DE⊥BC，DF⊥AC，∴DE＝DF（角平分线上的点到角的两边距离相等）∵∠DEC＝∠ECF＝∠CFD＝90°，∴四边形CFDE是矩形（有三个角是直角的四边形是矩形）∴四边形CFDE是正方形（有一组邻边相等的矩形是正方形） 课堂练习2、6、72、3、5、6、7、81、2、3、4、5、6、7、82、在下列性质中,平行四边形具有的是______________________矩形具有的是____________________________菱形具有的是____________________________正方形具有的是__________________________（1）四边都相等；（2）对角线互相平分；（3）对角线相等；（4）对角线互相垂直；（5）四个角都是直角；（6）每条对角线平分一组对角；（7）对边相等且平行；（8）既是轴对称图形,又是中心对称图形.1、2、4、6、7、8 课堂练习3、如图，在△ABC中，点D是边BC的中点，DE⊥AC、DF⊥AB，垂足分别是E、F，且BF=CE．（1）求证：DE=DF；（1）证明：∵DE⊥AC，DF⊥AB，∴∠BFD=∠CED=90°，在Rt△BDF和Rt△CDE中，∵BD=CD,BF=CF，∴Rt△BDF≌Rt△CDE（HL）∴DE=DF； 课堂练习3、如图，在△ABC中，点D是边BC的中点，DE⊥AC、DF⊥AB，垂足分别是E、F，且BF=CE．（2）当∠A=90°时，试判断四边形AFDE是怎样的四边形，并证明你的结论．（2）答：四边形AFDE是正方形．理由如下：∵∠A=90°，DE⊥AC，DF⊥AB，∴四边形AFDE是矩形，又∵DF=DE，∴四边形AFDE是正方形． 作业布置课本第26页习题6.8第1、2、3、4、5题 板书设计正方形矩形有一组邻边相等菱形有一个角是直角有一组邻边相等有一个角是直角平行四边形有一个角是直角有一组邻边相等