八年级上数学课件《实数》 (12)_苏科版

八年级上数学课件《实数》 (12)_苏科版

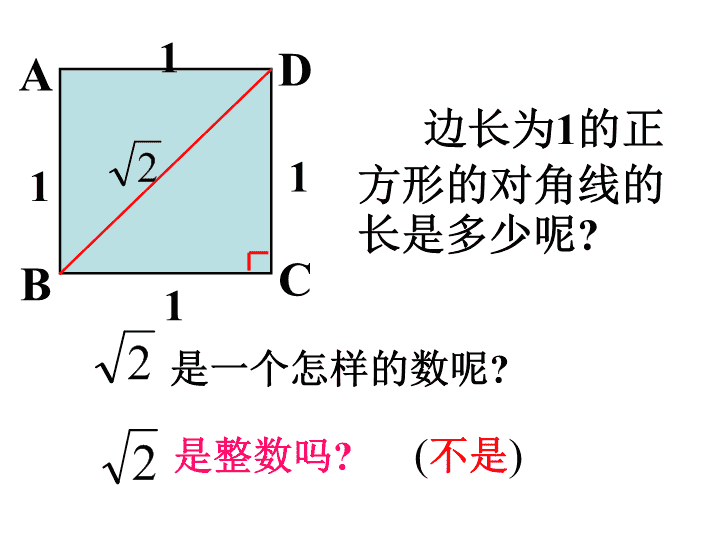
实数（1） 1111ACBD边长为1的正方形的对角线的长是多少呢?是一个怎样的数呢?是整数吗?(不是) 因为哪些分数的平方与2接近呢?讨论(1)是一个整数吗?(2)是一个分数吗? 因为所以 结论数学思想:无限逼近的数学思想 1.无理数的概念无限不循环小数称为无理数.两个条件:①无限小数;②不循环小数缺一不可注意 实数有理数无理数整数分数有限小数或无限循环小数无限不循环小数有理数和无理数统称为实数 实数正实数０负实数正有理数正无理数负无理数负有理数 有理数集合{…}无理数集合{…}正实数集合{…}负实数集合{…}0.01001000100001…0.01001000100001…0.01001000100001…牛刀小试: 2、判断：（1）无理数都是无限小数（）（2）无限小数都是无理数（）（3）两个无理数的和一定是无理数（）（）（）(6)整数和分数统称为有理数()√××××√ 3.下列语句中正确的是()A.带根号的数都是无理数B.不带根号的数都是有理数C.无理数一定是无限不循环小数D.无限小数一定是无理数C 有理数都可以用数轴上的点来表示，反过来，数轴上的点是否都表示有理数呢?能不能在数轴上找到一个点，它表示呢？ 0231-1在数轴上画出表示的点你能在数轴上画出表示的点吗?－　呢？ 每个实数都可以用数轴上的一个点来表示；反之，数轴上的每一个点都表示一个实数。实数与数轴上的点是一一对应的。结论: 4.(1)在数轴上找出表示的点.(2)在数轴上找出表示的点.O-3-2-1321 O-3-2-1321 2.把下列各数分别填入相应的集合中：整数集合分数集合有理数集合无理数集合············ 练一练1.和数轴上的点一一对应的数集是()A.有理数集B.无理数集C.整数集D.实数集2.在实数中整数有_______________________________;有理数有______________________________;无理数有_____________________________.D 这节课，我的收获是---无理数的常见形式:①π是无理数;②带根号且开方开不尽的数;③0.1010010001…通过“逼近”的数学思想,体会到无理数的存在实数与数轴上的点是一一对应的初次体会到“数形结合”的数学思想 实数有理数无理数整数零分数正无理数负无理数正整数负整数正分数负分数有限小数或无限循环小数无限不循环小数实数的分类：自然数 实数正实数负实数正有理数零负有理数正无理数负无理数还可如下分类会将一个数进行分类是重点能将一个无理数在数轴上表示出来是难点