八年级上数学课件《方差与标准差6.4 数据的离散程度 极差、方差和标准差》_北师大版

八年级上数学课件《方差与标准差6.4 数据的离散程度 极差、方差和标准差》_北师大版

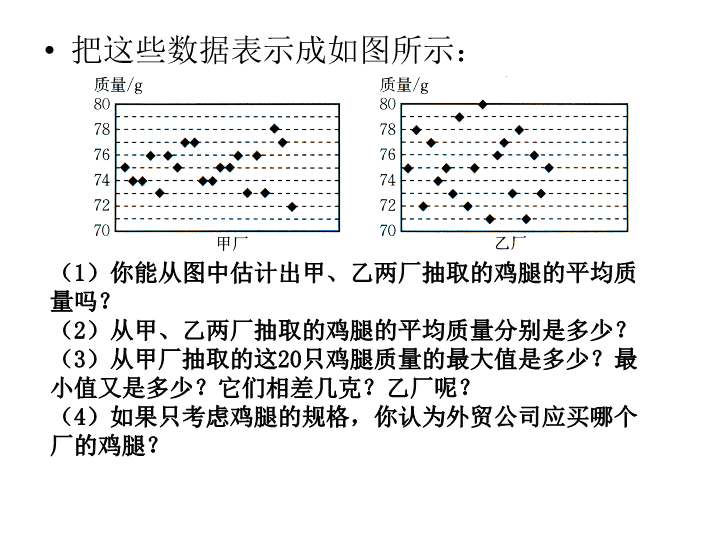
6.4数据的离散程度极差、方差和标准差 为了提高农副产品的国际竞争力，一些行业协会对农副产品的规格进行了划分。某外贸公司要出口一批规格为75g的鸡腿，现有2个厂家提供货源，他们的价格相同，鸡腿的品质也相近。质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿，他们的质量（单位：g）如下：甲厂：75，74，74，76，73，76，75，77，77，74，74，75，76，73，76，73，78，77，72；乙厂：75，78，72，77，74，75，73，79，72，75，80，71，76，77，73，78，71，76，73，75；情景导入 把这些数据表示成如图所示：（1）你能从图中估计出甲、乙两厂抽取的鸡腿的平均质量吗？（2）从甲、乙两厂抽取的鸡腿的平均质量分别是多少？（3）从甲厂抽取的这20只鸡腿质量的最大值是多少？最小值又是多少？它们相差几克？乙厂呢？（4）如果只考虑鸡腿的规格，你认为外贸公司应买哪个厂的鸡腿？ 解：甲厂20只鸡腿的平均质量：甲厂20之鸡腿质量的方差： 实际生活中,除了关心数据的集中趋势外,人们往往还关注数据的离散程度,即它们相对于集中趋势的偏离情况.一组数据中最大数据与最小数据的差（称为极差）,就是刻画数据离散程度的一个统计量.小结 如果丙厂也参与了竞争，从该厂抽样调查了20只鸡腿，数据如图所示：思考探究，获取新知（1）丙厂这20只鸡腿的平均数和极差分别是多少？（2）如何刻画丙厂这20只鸡腿的质量与其平均数的差距？分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距。（3）在甲、丙两厂中，你认为哪个厂的鸡腿质量更符合要求？为什么？ 数学上，数据的离散程度还可以用方差或标准差刻画.方差是各个数据与平均数差的平方的平均数,即结论其中,x是x1,x2,…,xn的平均数,s2是方差.而标准差就是方差的算术平方根.一般而言,一组数据的极差、方差或标准差越小，这组数据就越稳定. （1）计算从丙厂抽取的20只鸡腿质量的方差。（2）根据计算结果，你认为甲、丙两厂的产品哪个更符合规格？做一做 某日，A、B两地的气温如图所示：（1）不进行计算，说说A、B两地这一天气温的特点。（2）分别计算这一天A、B两地气温的平均数和方差，与你刚才的看法一致吗？ 1、数学课上,小明拿出了连贯五天日最低气温的统计表.那么,这组数据的平均数和极差分别是.运用新知，深化理解 2.一个样本为1,3,2,2,a,b,c已知这个样本的系数为3,平均数为2,那么这个样本的方差为.3.甲、乙两个样本，甲的样本方差是2.15，乙的样本方差是2.21，那么样本甲和样本乙的波动大小是（）A.甲、乙的波动大小一样B.甲的波动比乙的波动大C.乙的波动比甲的波动大D.无法比较 4.10名同学分成甲、乙两队进行篮球比赛，他们的身高（单位：cm）如下表所示： 5.新星公司到某大学招聘公司职员，对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试，三项的得分满分都为100分，三项的分数分别按5：3：2的比例记入每人的最后总分，有4位应聘者的得分如下表所示. （1）写出4位应聘者的总得分；（2）就表上专业知识、英语水平、参加社会实践与社团活动等三项的得分，分别求出三项中4人秘得分数的方差；（3）由（1）和（2），你对应聘者有何建议？ 1.回顾极差，方差的概念和计算公式等知识点.2.通过本节课的学习，你已经掌握了哪些知识？还有哪些疑问？与同学们交流.师生互动，课堂小结 按“on”开机按“mode”选择“SD”模式（按“2”）然后把你的一连串数据输入进去，例如：1,2,3,4这一组数据先输入1，然后按一下“M+”这时屏幕上会出现“n=1”的字样，继续输入每输入一个数据就要按一下“M+”例如：1,2,3,4这一组数据到最后屏幕应该显示“n=4”（这里的n表示数据个数）然后按“shift”再按“2”再选择“2”按“=”但这只是标准差所以再按“x²”再按“=”此时的答案就是所求数据的方差。用科学计算器算方差 1.布置作业：习题6.62、3、4题2.完成本课时的习题课后作业