八年级数学四边形复习与巩固

八年级数学四边形复习与巩固

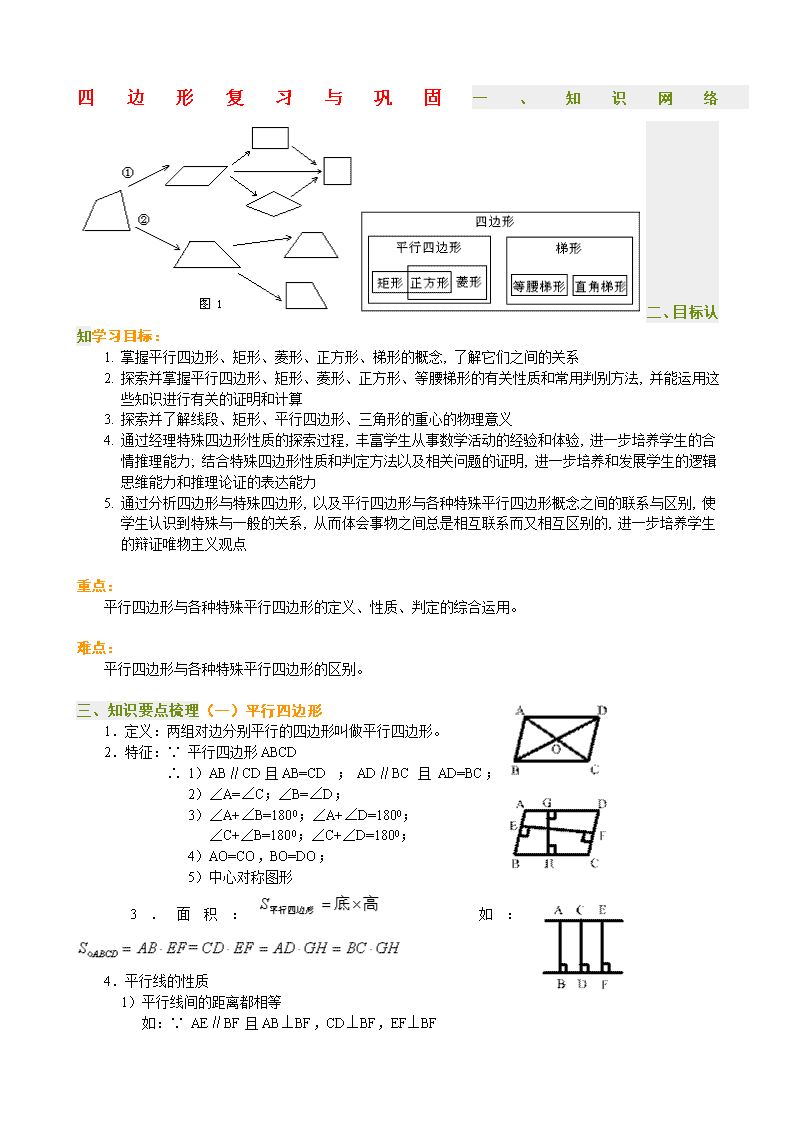
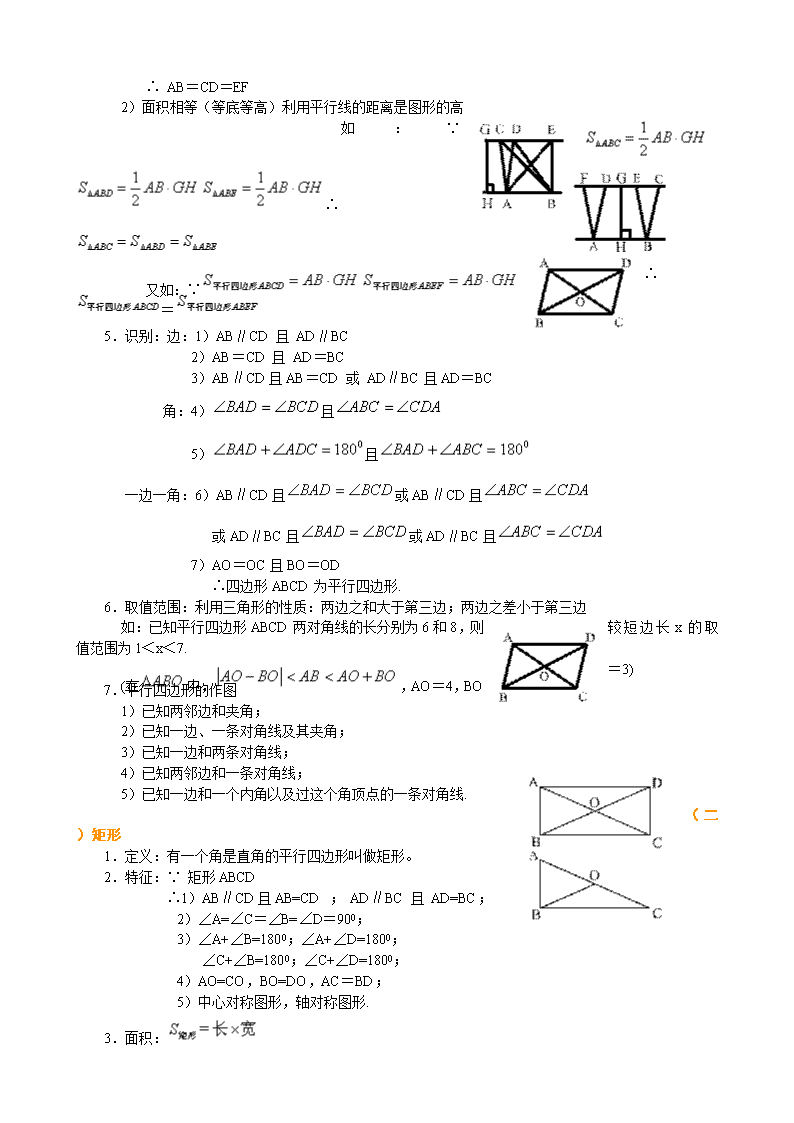
四边形复习与巩固一、知识网络二、目标认知学习目标：　　1.掌握平行四边形、矩形、菱形、正方形、梯形的概念,了解它们之间的关系　　2.探索并掌握平行四边形、矩形、菱形、正方形、等腰梯形的有关性质和常用判别方法,并能运用这　　　些知识进行有关的证明和计算　　3.探索并了解线段、矩形、平行四边形、三角形的重心的物理意义　　4.通过经理特殊四边形性质的探索过程,丰富学生从事数学活动的经验和体验,进一步培养学生的合　　　情推理能力;结合特殊四边形性质和判定方法以及相关问题的证明,进一步培养和发展学生的逻辑　　　思维能力和推理论证的表达能力　　5.通过分析四边形与特殊四边形,以及平行四边形与各种特殊平行四边形概念之间的联系与区别,使　　　学生认识到特殊与一般的关系,从而体会事物之间总是相互联系而又相互区别的,进一步培养学生　　　的辩证唯物主义观点重点：　　平行四边形与各种特殊平行四边形的定义、性质、判定的综合运用。难点：　　平行四边形与各种特殊平行四边形的区别。三、知识要点梳理（一）平行四边形　　1．定义：两组对边分别平行的四边形叫做平行四边形。　　2．特征：∵平行四边形ABCD　　　　　　∴1）AB∥CD且AB=CD；AD∥BC且AD=BC；　　　　　　　　2）∠A=∠C；∠B=∠D；　　　　　　　　3）∠A+∠B=1800；∠A+∠D=1800；　　　　　　　　　∠C+∠B=1800；∠C+∠D=1800；　　　　　　　　4）AO=CO，BO=DO；　　　　　　　　5）中心对称图形　　3．面积：　　　如：　　4．平行线的性质　　　1）平行线间的距离都相等　　　　如：∵AE∥BF且AB⊥BF，CD⊥BF，EF⊥ BF　　　　　∴AB＝CD＝EF　　　2）面积相等（等底等高）利用平行线的距离是图形的高　　　　　如：∵∴　　　　　又如：∵∴＝　　5．识别：边：1）AB∥CD且AD∥BC　　　　　　　　2）AB＝CD且AD＝BC　　　　　　　　3）AB∥CD且AB＝CD或AD∥BC且AD＝BC　　　　　　角：4）且　　　　　　　　5）且　　　一边一角：6）AB∥CD且或AB∥CD且　　　　　　　　　或AD∥BC且或AD∥BC且　　　　　　　　7）AO＝OC且BO＝OD　　　　　　　　　∴四边形ABCD为平行四边形.　　6．取值范围：利用三角形的性质：两边之和大于第三边；两边之差小于第三边　　　如：已知平行四边形ABCD两对角线的长分别为6和8，则较短边长x的取值范围为1＜x＜7.　　　(在中，，AO＝4，BO＝3)　　7．平行四边形的作图　　　1）已知两邻边和夹角；　　　2）已知一边、一条对角线及其夹角；　　　3）已知一边和两条对角线；　　　4）已知两邻边和一条对角线；　　　5）已知一边和一个内角以及过这个角顶点的一条对角线.（二）矩形　　1．定义：有一个角是直角的平行四边形叫做矩形。　　2．特征：∵矩形ABCD　　　　　　∴1）AB∥CD且AB=CD；AD∥BC且AD=BC；　　　　　　　2）∠A=∠C＝∠B=∠D＝900；　　　　　　　3）∠A+∠B=1800；∠A+∠D=1800；　　　　　　　　　∠C+∠B=1800；∠C+∠D=1800；　　　　　　　4）AO=CO，BO=DO，AC＝BD；　　　　　　　5）中心对称图形，轴对称图形.　　3．面积： 　　　如：　　4．由矩形得直角三角形的性质：　　　1）直角三角形斜边上的中线等于斜边的一半.　　　　如：∵在中，且AO＝CO　　　　　　∴BO=AO=CO=　　　2）直角三角形中，30度角所对应的直角边等于斜边的一半.　　　　如：∵在中，且∴AB=AO=CO=　　5．识别：1)先证明它是平行四边形　　　　　　2）再加：有一个角是直角或者对角线相等即可.　　　　如：1）①四边形ABCD为平行四边形ABCD②　　　　　　2）①四边形ABCD为平行四边形ABCD②AC=BD　　　　　　　∴平行四边形ABCD为矩形.（三）菱形　　1．定义：有一组邻边相等的平行四边形叫做菱形.　　2．特征：∵菱形ABCD∴1）AB∥CD，AD∥BC，AB=CD＝AD=BC；　　　　　　　2）∠BAD=∠BCD；∠ABC=∠ADC；　　　　　　　3）∠BAD+∠ABC=1800；∠BAD+∠ADC=1800；　　　　　　　　∠BCD+∠ABC=1800；∠BCD+∠ADC=1800；　　　　　　　4）AO=CO，BO=DO，，对角线平分对角；　　　　　　　5)∠BAO＝∠DAO；∠BCO＝∠DCO；∠ABO＝∠CBO；∠ADO＝∠CDO.　　　　　　　6）中心对称图形，轴对称图形.　　3．面积：　　　如：　　4．识别：1）先证明它是平行四边形2）再加：有一组邻边相等或对角线互相垂直即可　　　如：1）①四边形ABCD为平行四边形ABCD②AB＝AD或AB＝BC或AD＝DC或BC＝CD　　　　　2）①四边形ABCD为平行四边形ABCD②AC⊥BD（四）正方形　　1．定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形.　　2．特征：∵ 正方形ABCD　　　　　　∴1）AB∥CD，AD∥BC，AB=CD＝AD=BC；　　　　　　　2）∠BAD＝∠BCD＝∠ABC=∠ADC＝900；　　　　　　　3）∠BAD+∠ABC=1800；∠BAD+∠ADC=1800；　　　　　　　　∠BCD+∠ABC=1800；∠BCD+∠ADC=1800；　　　　　　　4）AO=CO，BO=DO，AC=BD，，对角线平分对角；　　　　　　　5)∠BAO＝∠DAO＝∠BCO＝∠DCO＝∠ABO＝∠CBO＝∠ADO＝∠CDO＝450.　　　　　　　6）中心对称图形，轴对称图形.　　3．面积：　　4．识别：1）先证是平行四边形；2）再证是矩形或菱形；3）再加菱形或矩形的特征　　　如：1）①四边形ABCD为平行四边形ABCD②AB＝AD或AB＝BC或AD＝DC或BC＝CD，　　　　　　　　平行四边形ABCD为菱形③　　　　　2）①四边形ABCD为平行四边形ABCD②AB＝AD或AB＝BC或AD＝DC或BC＝CD，　　　　　　　平行四边形ABCD为菱形③AC＝BD　　　　　3）①四边形ABCD为平行四边形ABCD②AC⊥BD，平行四边形ABCD为菱形③　　　　　4）①四边形ABCD为平行四边形ABCD②AC⊥BD，平行四边形ABCD为菱形③AC＝BD　　　　　5）①四边形ABCD为平行四边形ABCD②，平行四边形ABCD为矩形　　　　　　③AB＝AD或AB＝BC或AD＝DC或BC＝CD　　　　　6）①四边形ABCD为平行四边形ABCD②，平行四边形ABCD为矩形③AC⊥BD　　　　　7）①四边形ABCD为平行四边形ABCD②AC＝BD，平行四边形ABCD为矩形③AB＝AD或AB＝BC或　　　　　　　AD＝DC或BC＝CD　　　　　8）①四边形ABCD为平行四边形ABCD②AC＝BD，平行四边形ABCD为矩形③AC⊥BD（五）梯形　　1．定义：一组对边平行而另一组对边不平行的四边形叫梯形；有一个角是直角的梯形叫直角梯形；　　　有两条腰相等的梯形叫做等腰梯形.　　2．特征（等腰梯形）：在等腰梯形ABCD中　　　1）AD∥BC，AB＝CD；　　　2）∠ABC=∠BCD，∠BAD=∠CDA；　　　3）AC＝BD；4）轴对称图形　　3．面积：　　4．识别：1）若AD∥BC且AD≠BC，则四边形ABCD为梯形；　　　　　　2）若AB＝CD或∠ABC=∠BCD或AC＝BD，则梯形ABCD为等腰梯形ABCD.　　　　　　3）等腰梯形的性质和判定：　　　① 性质：等腰梯形在同一底边上的两个内角相等，两腰相等，两底平行，两对角线相等，是轴对称　　　　图形，只有一条对称轴（底的中垂线就是它的对称轴）．　　　②判定方法：两腰相等的梯形是等腰梯形；同一底边上的两个角相等的梯形是等腰梯形；对角线相　　　　等的梯形是等腰梯形．　　　　　　4）直角梯形　　　　　　　有一个角是直角的梯形叫做直角梯形．　　　　5.解决梯形问题的常用方法（如下图所示）：　　①“作高”：使两腰在两个直角三角形中．　　②“移对角线”：使两条对角线在同一个三角形中．　　③“廷腰”：构造具有公共角的两个三角形．　　④“等积变形”：连接梯形上底一端点和另一腰中点，并延长交下底的延长线于一点，构成三角形．　　综上，解决梯形问题的基本思路：梯形问题三角形或平行四边形问题，这种思路常通过平移或旋转来实现．四、规律方法指导　　1、转化思想（又叫化归思想）　　　　转化思想就是将复杂的问题转化为简单的问题，或将陌生的问题转化为熟悉的问题来处理的一种思　　　　想，本章应用化归思想的内容主要有两个方面：　　（1）四边形问题转化为三角形问题来处理．　　（2）梯形问题转化为三角形和平行四边形来处理．　　2、代数法（计算法）　　　　代数法是用代数知识来解决几何问题的方法，也就是说运用几何定理、法则，通过列方程、方程组　　　　或不等式及解方程、方程组、恒等变形等代数方法，把几何问题转化成代数问题来解决的方法．　　3、变换思想　　　　即运用平移变换、旋转变换、对称变换等方法来构造图形解决几何问题．　　4、应注意的几个问题　　（1）不能把判定方法与性质混淆，应加深对判定方法中条件的理解，重视判定方法中的基本图形，不　　　　要用性质代替了判别．解题时不能想当然，更不要忽视重要步骤．　　（2）在判别一个四边形是正方形时，容易忽视某个条件，致使判断失误，要避免这种错误的产生就必　　　　须认真熟记正方形的定义、特征和识别方法，认真区别各个特征、识别方法的条件，不要忽略隐　　　　含条件，避免错误的产生．　　（3）判别一个四边形是等腰梯形时，不要忽略了先判别四边形是梯形，对梯形的概念、性质、判定认　 　　　识要清．　　（4）纵横对比，分清各种四边形的从属关系，抓住其概念的内涵．　　（5）复习时，依然从边、角、对角线、对称性等角度来理解和应用平行四边形、矩形、菱形、正方形　　　　的性质和判定方法，注意对问题的观察、分析与总结．