北师大版七年级数学（下册）第四章测试卷（附参考答案）

北师大版七年级数学（下册）第四章测试卷（附参考答案）

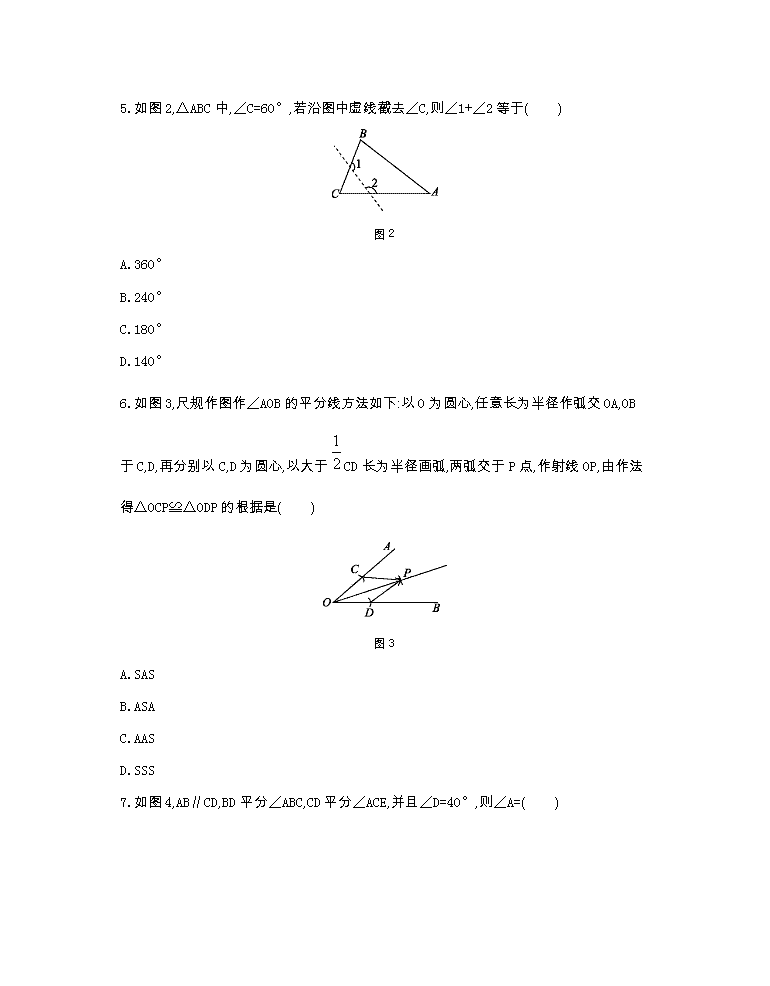
数学七下北师测试卷第四章 ‎1.已知三角形的两边a=4,b=8,则下列长度的四条线段中能作为第三边c的是(　　)‎ A.3‎ B.4‎ C.7‎ D.12‎ ‎2.一扇窗户打开后,用窗钩可将其固定,这里所运用的几何原理是(　　)‎ A.三角形具有稳定性 B.两点之间线段最短 C.两点确定一条直线 D.垂线段最短 ‎3.知一个等腰三角形的两边长分别为2和1,则此等腰三角形的周长为(　　)‎ A.5‎ B.4‎ C.3‎ D.5或4‎ ‎4.如图1,∠B+∠C+∠D+∠E-∠A等于(　　)‎ 图1‎ A.360°‎ B.300°‎ C.180°‎ D.240°‎ ‎5.如图2,△ABC中,∠C=60°,若沿图中虚线截去∠C,则∠1+∠2等于(　　)‎ 图2‎ A.360°‎ B.240°‎ C.180°‎ D.140°‎ ‎6.如图3,尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径作弧交OA,OB于C,D,再分别以C,D为圆心,以大于CD长为半径画弧,两弧交于P点,作射线OP,由作法得△OCP≌△ODP的根据是(　　)‎ 图3‎ A.SAS B.ASA C.AAS D.SSS ‎7.如图4,AB∥CD,BD平分∠ABC,CD平分∠ACE,并且∠D=40°,则∠A=(　　)‎ 图4‎ A.50°‎ B.60°‎ C.70°‎ D.80°‎ ‎8.如图5,AC=BD,AB=CD,图中的全等三角形的对数是(　　)‎ 图5‎ A.2对 B.3对 C.4对 D.5对 ‎9.如图6,观察下列图形,则第n个图形中三角形的个数是(　　)‎ ‎　　　　　　…　‎ 图6‎ A.2n+2‎ B.4n+4‎ C.4n-4‎ D.4n ‎10.如图7所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,AD=3,则点D到BC的距离是(　　)‎ ‎　　　‎ ‎　　　　　　　　　　　　　　　　　　　图7‎ A.3‎ B.4‎ C.5‎ D.6‎ ‎11.如图8为两个全等的三角形,则∠C的对应角为　　. ‎ 图8‎ ‎12.将一副三角尺按如图9所示叠放在一起,则∠α的度数为　　. ‎ 图9‎ ‎13.如图10,已知方格中是4个相同的正方形,则∠1+∠2+∠3=　　度. ‎ 图10‎ ‎14.某风景区改造中,需测量湖两岸游船码头A,B间的距离(如图11),于是工作人员在AB的垂线AF上取两点E,D,使ED=AE,再过点D作出AF的垂线OD,并在OD上找一点C,使B,E,C在同一直线上,这时测量CD的长是15米,由此可知A,B的距离是　　. ‎ 图11‎ ‎15.如图12,在4×5的正方形网格中,已知顶点在格点上的△ABC,现在要在其他的格点中选择点D,使△ABC与△ABD全等,这样的格点一共有　　个. ‎ 图12‎ ‎16.如图13,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角的度数是　　. ‎ 图13‎ ‎17.如图14,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,可补充的条件是　　.(写出一个即可) ‎ 图14‎ ‎18.用直尺和圆规作一个角等于已知角的示意图如图15所示,则要说明∠D’O’C’=∠DOC,需要证明△D’O’C’≌△DOC,则这两个三角形全等的依据是　　(写出全等的简写).‎ 图15‎ ‎19.如图16所示,方格中有一个△ABC,请你在方格内,画出满足条件A1B1=AB,B1C1=BC,∠A1=∠A的△A1B1C1,并判断△A1B1C1与△ABC是否一定全等?‎ 图16‎ ‎20.等边三角形给人以“稳如泰山”的美感,它有独特的性质,请按照下列要求分别在各图中画出分割线.‎ ‎(1)把图17①分割成两个全等三角形;‎ ‎(2)把图17②分割成三个全等三角形;‎ ‎(3)把图17③分割成四个全等三角形.‎ 图17‎ ‎21.如图18,在△ABC中,∠B=∠C,点F为AC上一点,FD⊥BC于点D,过D点作DE⊥AB于点E,若∠AFD=158°,求∠EDF的度数.‎ 图18‎ ‎22.已知:如图19,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.‎ 图19‎ ‎23.如图20,在△ABC中,AC=BC,AC⊥BC,AE⊥CD,垂足为点E,BF⊥CD,垂足为点F,图中BF与哪条线段相等?请说明为什么.‎ 图20‎ ‎24.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题:小溪边长着两棵棕榈树,恰好隔岸相望(如图21),一棵树(AB)高是30尺,另一棵树(CD)高是20尺,两棵树树干间的距离(BD)是50尺,两棵树的树顶(A,C)处各站着一只鸟,忽然,两只鸟同时看见两树间的水面上(E处)游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且路线垂直,最终同时到达目标,问这条鱼出现的地方(E点)离比较高的棕榈树(AB)的树根(B点)有多远?‎ 图21‎ 参考答案 ‎1.C ‎2.A ‎3.A ‎4.C ‎5.B ‎6.D ‎7.D ‎8.B ‎9.D ‎10.A ‎11.∠AED ‎12.105°‎ ‎13.135‎ ‎14.15米 ‎15.3‎ ‎16.40°‎ ‎17.AC=AE或∠C=∠E或∠B=∠D ‎18.SSS ‎19.不一定全等.如图所示:‎ ‎20.图略.(1)过一顶点作对边垂线;(2)三条中线的交点到三个顶点连线构成了三个全等三角形;(3)连接三条边的中点,得到四个全等三角形.‎ ‎21.解:因为AB=AC,‎ 所以∠B=∠C.‎ 因为FD⊥BC于点D,DE⊥BC于点E,‎ 所以∠BED=∠FDC=90°.‎ 因为∠AFD=158°,‎ 所以∠EDB=∠CFD=180°-158°=22°.‎ 所以∠EDF=90°-∠EDB=90°-22°=68°.‎ ‎22.求证:△ABC≌△CDE.‎ 证明:因为AC∥DE,‎ 所以∠ACD=∠D,∠BCA=∠E.‎ 又因为∠ACD=∠B,‎ 所以∠B=∠D.‎ 又因为AC=CE,‎ 所以△ABC≌△CDE.‎ ‎23.解:BF=CE.‎ 理由:因为AC⊥BC,AE⊥CD,‎ 所以∠CAE+∠ACE=90°,‎ ‎∠BCF+∠ACE=90°,‎ 所以∠CAE=∠BCF.‎ 又因为∠AEC=∠CFB=90°,AC=BC,‎ 所以△ACE≌△CBF(AAS),‎ 所以BF=CE.‎ ‎24.解:依题意可知CE=AE,CE⊥AE,‎ 所以∠CED+∠AEB=90°.‎ 又因为CD⊥BD,AB⊥BD,‎ 所以∠CDE=∠EBA=90°,‎ 所以∠CED+∠C=90°,‎ 所以∠C=∠AEB.‎ 在△CDE和△EBA中,‎ 所以△CDE≌△EBA(AAS),‎ 所以EB=CD=20(尺).‎