探索三角形全等的条件　　教案(1)

探索三角形全等的条件　　教案(1)

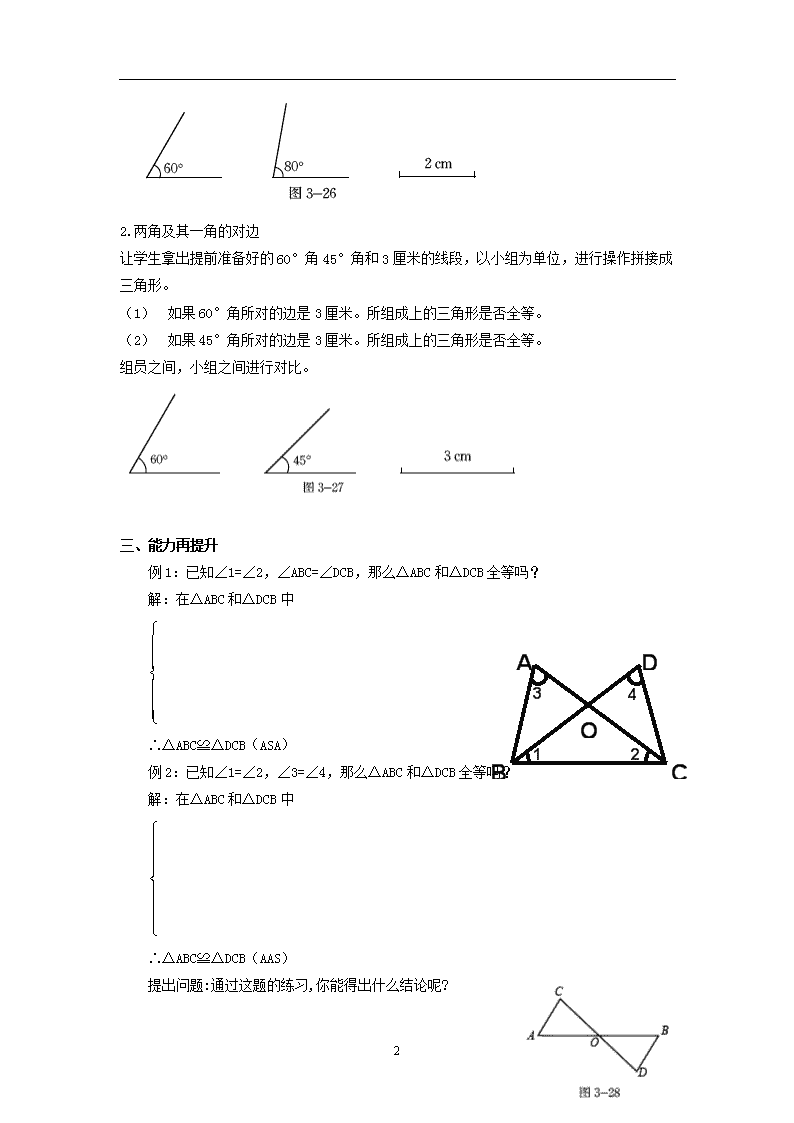
‎ ‎ 第三章 三角形 ‎3.3.2 探索三角形全等的条件 ‎【教学目标】‎ 知识与技能 ‎1．经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；‎ ‎2．掌握三角形的“角边角”“角角边”条件，了解三角形的稳定性。‎ 过程与方法 学生经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程，由此带动知识发生、发展的全过程。‎ 情感态度与价值观 学生善于观察生活发生的事情，并愿意解决提出的难题，在实践反思中敢于发表自己的观点，树立实事求是的科学态度。‎ 行为与创新 学生积极参与三角形全等条件的探究过程，从中体味全作与成功的快乐，建立学习好数学的自信心，体会三角形全等条件在现实生活中的应用价值。‎ ‎【教学重难点】‎ 重点 探索三角形全等的条件 难点 利用三角形全等的条件判断两个三角形是否全等 ‎【课前准备】 教师：课件 学生：练习本.‎ ‎【教学过程】‎ 复习回顾 用自己的语言描述“SSS”的判定方法。‎ 一、创设情景引入 有一块三角形纸片撕去了一个角,要去剪一块 新的,如果你手头没有测量的仪器,你能保证新 剪的纸片形状、大小和原来的一样吗?‎ 这个问题让学生议论后回答,他们的答案或许只是一种感觉,于是教师引导学生,抓住问题的本质:三角形的三个元素---两个角一条边.‎ 二、应用练习 促进深化 ‎1.角边角 让学生拿出提前准备好的60°角80°角和2厘米的线段，以小组为单位，进行操作拼接成三角形，再进行对比，看一看组成的三角形是否全等。‎ 4‎ ‎ ‎ ‎2.两角及其一角的对边 让学生拿出提前准备好的60°角45°角和3厘米的线段，以小组为单位，进行操作拼接成三角形。‎ （1） 如果60°角所对的边是3厘米。所组成上的三角形是否全等。‎ （2） 如果45°角所对的边是3厘米。所组成上的三角形是否全等。‎ 组员之间，小组之间进行对比。‎ 三、能力再提升 例1：已知∠1=∠2，∠ABC=∠DCB，那么△ABC和△DCB全等吗？‎ A B C D O ‎1‎ ‎2‎ ‎3‎ ‎4‎ 解：在△ABC和△DCB中 ‎∴△ABC≌△DCB（ASA）‎ 例2：已知∠1=∠2，∠3=∠4，那么△ABC和△DCB全等吗？‎ 解：在△ABC和△DCB中 ‎∴△ABC≌△DCB（AAS）‎ 提出问题:通过这题的练习,你能得出什么结论呢?‎ 4‎ ‎ ‎ ‎(小组讨论,派代表回答)‎ 例3．如图3-28所示，AB与CD相交与点O，O是AB的中点，∠A=∠B,△AOC与△BOD全等吗？为什么？‎ 补充练习 ‎1﹑请在下列空格中填上适当的条件，使△ABC≌△DEF。‎ 在△ABC和△DEF中 ‎ ‎ ‎∴△ABC ≌△DEF（ ）‎ A B C D E F ‎2﹑如图，已知，∠C＝∠E，∠1＝∠2，AB＝AD，△ABC和△ADE全等吗？为什么？‎ A B C D E ‎1‎ ‎2‎ 四、归纳小结 通过这堂课的学习你有什么收获?知道了哪些新知识？学会了做什么？‎ 五、本课作业 P85 知识技能2.3。问题解决。‎ 课时作业设计 ‎1.如图,已知MB＝ND,∠MBA＝∠NDC,下列不能判定△ABM≌△CDN的条件是（　　）‎ A．∠M＝∠N　　B．AB＝CD　　‎ C．AM＝CN　　　D．AM∥CN ‎2. 在△ABC和△EMN中，已知∠A＝50°，∠B＝60°，∠E＝70°，∠M＝60°，AC＝EN 4‎ ‎ ‎ ‎，则这两个三角形（ ）‎ A.一定全等 B.一定不全等 ‎ C.不一定全等 D.以上都不对 ‎3. △ABC和△DEF中,AB=DE,∠B=∠E,补充条件后仍不一定能保证△ABC≌△DEF,则补充的这个条件为（ ）‎ A.BC=EF B.∠A=∠D C.AC=DF D.∠C=∠F ‎4.已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB的平分线．求证：AB=DC.‎ 答案：‎ ‎1.C 2.A 3.C 4.∵AC平分∠BCD，BD平分∠ABC,∴,,又∵∠ABC=∠DCB，∴∠ACB=∠CBD.在△ABC与△DCB中 ‎ ∴△ABC≌△DCB(A.A.S.) ‎ ‎∴AB=DC. ‎ 4‎