- 2021-10-25 发布 |
- 37.5 KB |
- 22页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级下数学课件:5-3-1 平行线的性质 (共22张PPT)_人教新课标
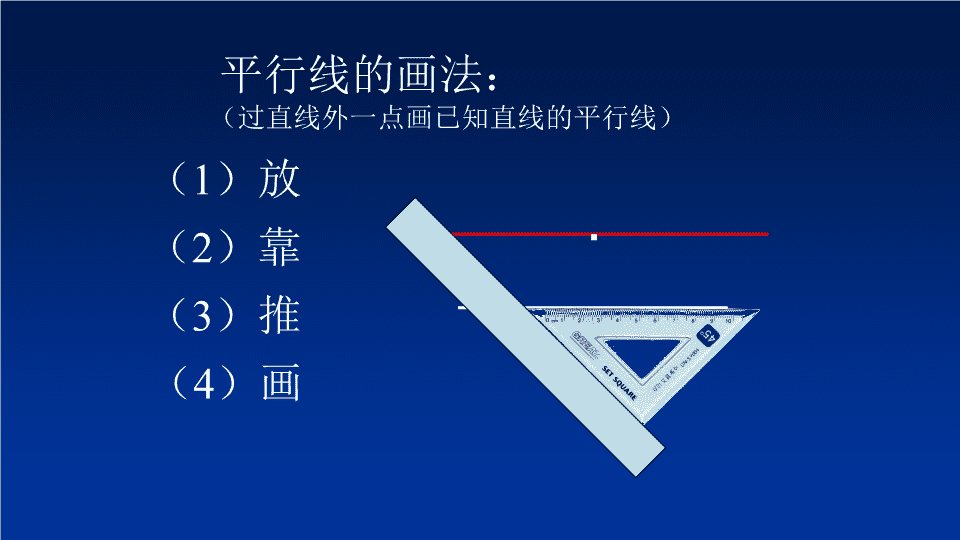
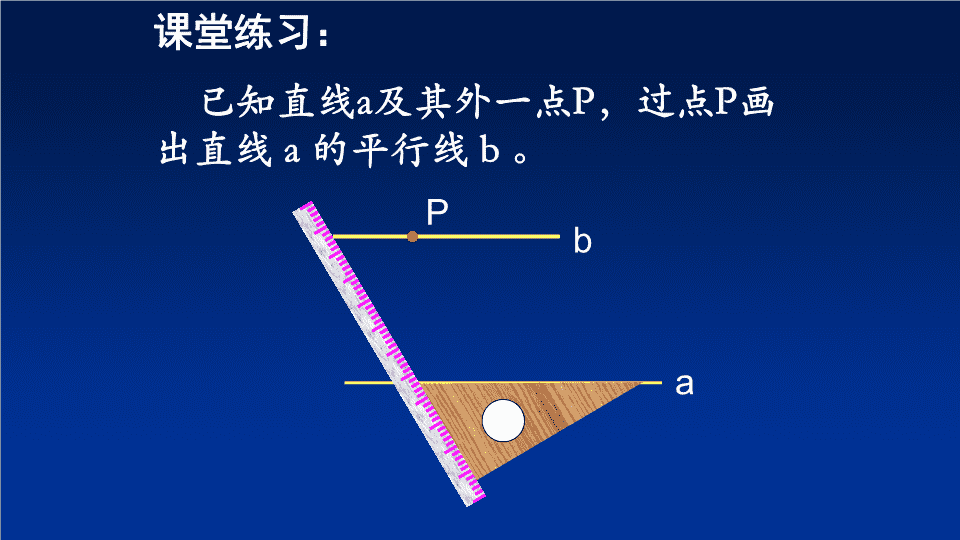
平行线的画法: (过直线外一点画已知直线的平行线) (1)放 (2)靠 (3)推 (4)画 · a P 课堂练习: 已知直线a及其外一点P,过点P画 出直线 a 的平行线 b 。 b 平行线的判定方法有哪三种? 它们是先知道什么? 后知道什么? 同位角相等 内错角相等 同旁内角互补 问题1 根据同位角相等,或者内错角相等, 或者同旁内角互补,可以判定两条直线 平行。 问题2 反过来,如果两直线平行,同位角、 内错角、同旁内角各有什么关系呢? (1)在我们刚才画的一组平行线a∥b 的 基础上,再画一条截线c,使之与直线 a ,b 相交,并标出所形成的八个角. (2)测量上面八个角的大小,记录下 来.从中你能发现什么? a 1 b c 12 3 4 56 8 7 (1)在我们刚才画的一组平行线a∥b的基础上,再画一条截线c, 使之与直线 a ,b 相交,并标出所形成的八个角. (2)测量上面八个角的大小,记录下来.从中你能发现什么? 说出你的猜想:两条平行线被第三条直线所截,同位 角 ,内错角 , 同旁内角 . 如果直线a与b不平行,你的猜想还成立吗? a b c 问题 如果两条直线平行,那么这两条平行线被 第三条直线所截而成的同位角有什么数量关系? 2 1 1 2 3 a b 回答 如图,已知:a// b 那么2与3有什么关系? 平行线的性质2: 两条平行线被第三条直线所截,内错角相等 。 简单说成:两直线平行,内错角相等。 例如:如右图 因为 a∥b, 所以 ∠1= ∠2( ) 又因为∠1 = ___(对顶角相等), 所以∠ 2 = ∠3. 两直线平行,同位角相等 ∠3 平行线的性质1(公理):两直线平行,同位角相等。 c 2 3 1 b a 解: a//b (已知) 1= 2(两直线平行,同位角相等) 1+ 3=180°(邻补角定义) 2+ 3=180°(等量代换) 如图:已知a//b, 那么2与 3有什么关系呢? 平行线的性质3 两条平行线被第三条直线所截,同旁内角互补。 简单说成:两直线平行,同旁内角互补。 平行线的性质1(公理):两直线平行,同位角相等。 平行线的性质2(公理):两直线平行,内错角相等。 4 平行线的性质 (1)两条平行线被第三条直线所截,同位角相等; (2)两条平行线被第三条直线所截,内错角相等; (3)两条平行线被第三条直线所截,同旁内角互补。 (1)两直线平行,同位角相等; 简单地说,就是: (2)两直线平行,内错角相等; (3)两直线平行,同旁内角互补。 例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯 形上底的一部分(如图)。要订造一块新的玻璃,已经 量得 ,你想一想,梯形另外两个角 各是多少度? 解:因为梯形上.下底互相平行,所以 梯形的另外两个 角分别是 100,115 DA A D B C., 互补与互补与 CDBA ,65115-180B 于是 .80100180 C .80,65 例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯 形上底的一部分(如图)。要订造一块新的玻璃,已经 量得 ,你想一想,梯形另外两个角 各是多少度? 解: ∵ AD∥BC (梯形的定义) 100,115 DA A D B C ∴ ∠A+∠B=180°(两直线平行,同旁内角互补) ∠D+∠C=180°(两直线平行,同旁内角互补) ∴ ∠B=180°-115 °= 65 ° ∠C=180°-100 °= 80 ° 又∵ ∠A=115° ,∠D=100°(已知) 练习 1.如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少 度? 解: ∵ ∠1= 54°(已知) ∴ ∠2=∠1 =54°(对顶角相等) ∵ a∥b(已知) ∴ ∠2+∠3=180°(两直线平行,同旁内角互补) ∴ ∠3= 180°- ∠2= 180° -54°=126° ∠4=∠1=54°(两直线平行,同位角相等) 1 2 3 4 a b ED C B A (已知)解:(1)∵∠ADE=60 ° ∠B=60 ° ∴∠ADE=∠B (等量代换) ∴DE∥BC (同位角相等,两直线平行) (2)∵ DE∥BC (已证明) ∴∠C= ∠ AED=40 ° (两直线平行,同位角相等) 又∵∠AED=40° (已知) 2.如图,D是AB上一点,E是AC上一点,∠ADE=60 ° ∠B=60 °∠AED=40° (1)DE和BC平行吗?为什么? (2) ∠C是多少度,为什么? 平行线的“判定”与“性质”有什么不同比一比 同位角相等 内错角相等 同旁内角互补 判定 已知 得到 得到 已知 小结: 图形 已知 结果 结论 同 位 角 内 错 角 同 旁 内 角 两直线平行 同旁内角互补 1 2 23 24 ) ) ) ) ) ) a b a b a b c c c 平行线的性质 小结 a//b 21 两直线平行 同位角相等 a//b 23 两直线平行 内错角相等 a//b )42( 18042 互补与 查看更多