七年级下册数学第四章 三角形 周周测5（4-2~4-3） 北师大版

七年级下册数学第四章 三角形 周周测5（4-2~4-3） 北师大版

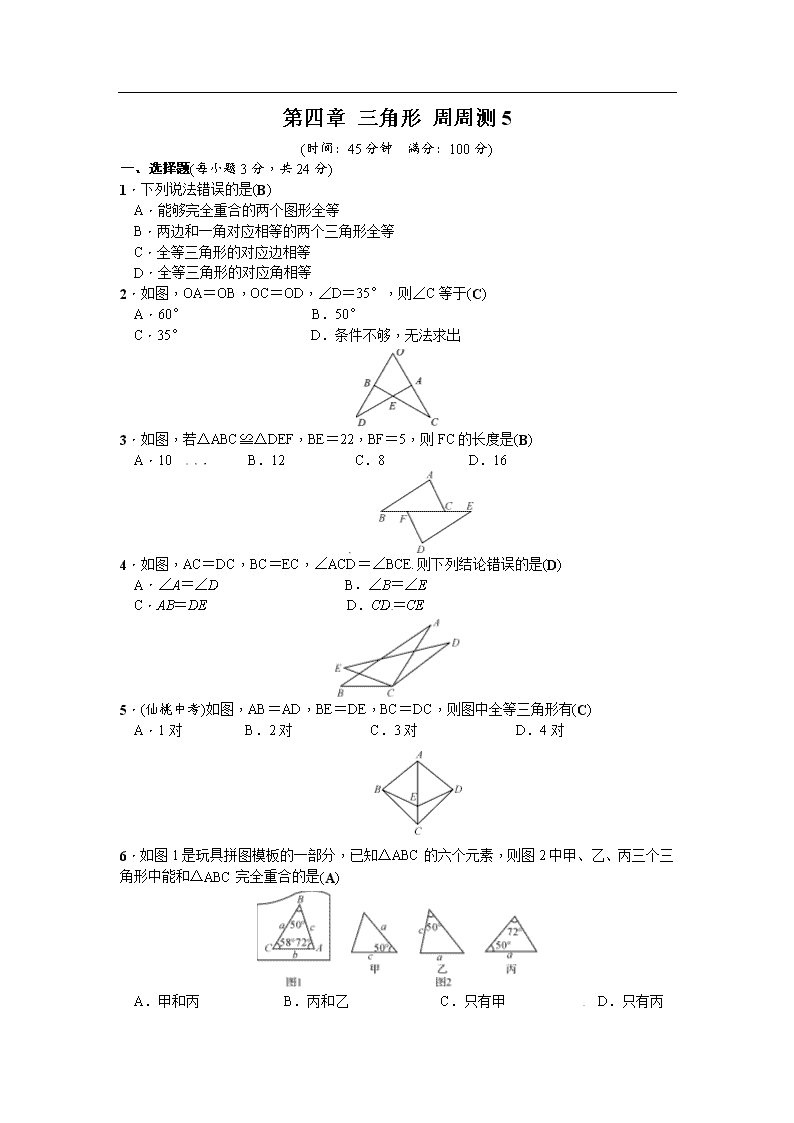
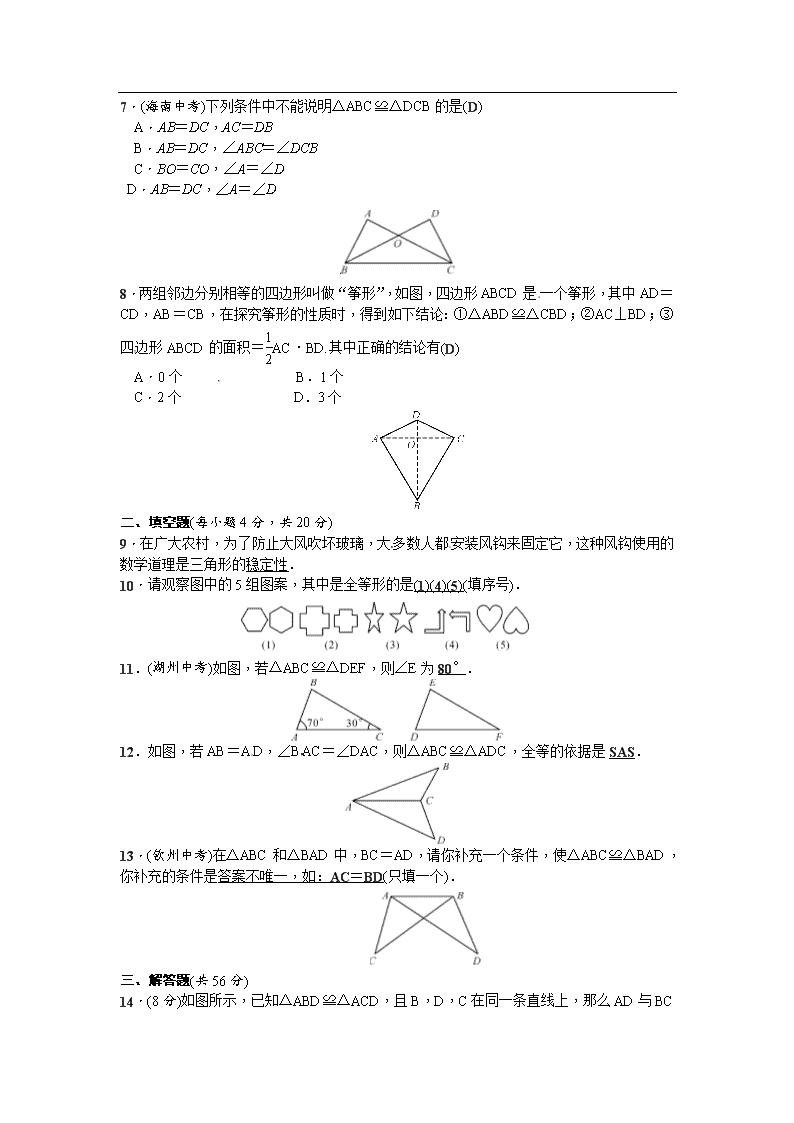
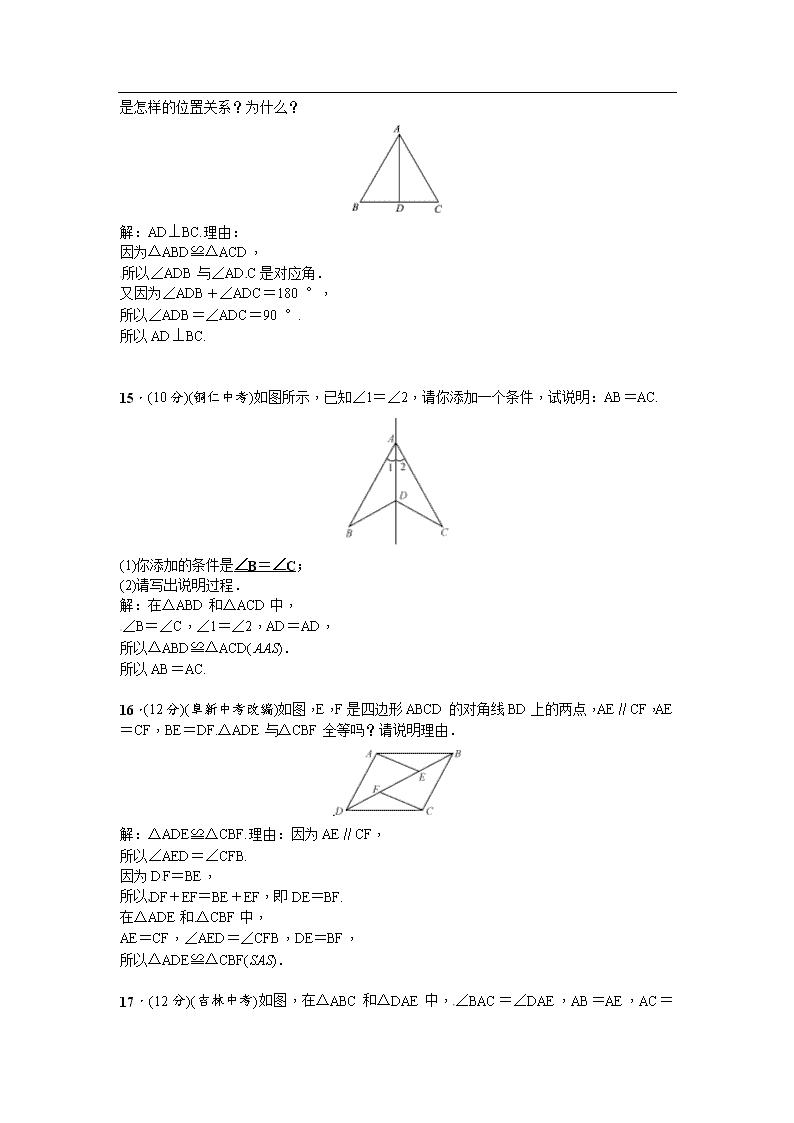
第四章 三角形 周周测5‎ ‎(时间：45分钟　满分：100分)‎ 一、选择题(每小题3分，共24分)‎ ‎1．下列说法错误的是(B)‎ ‎ A．能够完全重合的两个图形全等 ‎ B．两边和一角对应相等的两个三角形全等 ‎ C．全等三角形的对应边相等 ‎ D．全等三角形的对应角相等 ‎2．如图，OA＝OB，OC＝OD，∠D＝35°，则∠C等于(C)‎ ‎ A．60° B．50°‎ ‎ C．35° D．条件不够，无法求出 ‎3．如图，若△ABC≌△DEF，BE＝22，BF＝5，则FC的长度是(B)‎ ‎ A．10 B．12 C．8 D．16‎ ‎　　　　‎ ‎4．如图，AC＝DC，BC＝EC，∠ACD＝∠BCE.则下列结论错误的是(D)[来源:学&科&网Z&X&X&K]‎ ‎ A．∠A＝∠D B．∠B＝∠E ‎ C．AB＝DE D．CD＝CE ‎5．(仙桃中考)如图，AB＝AD，BE＝DE，BC＝DC，则图中全等三角形有(C)‎ ‎ A．1对 B．2对 C．3对 D．4对[来源:学。科。网]‎ ‎　　　‎ ‎6．如图1是玩具拼图模板的一部分，已知△ABC的六个元素，则图2中甲、乙、丙三个三角形中能和△ABC完全重合的是(A)‎ ‎ A．甲和丙 B．丙和乙 C．只有甲 D．只有丙 ‎7．(海南中考)下列条件中不能说明△ABC≌△DCB的是(D)‎ ‎ A．AB＝DC，AC＝DB ‎ B．AB＝DC，∠ABC＝∠DCB ‎ C．BO＝CO，∠A＝∠D ‎ D．AB＝DC，∠A＝∠D ‎8．两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD＝CD，AB＝CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积＝AC·BD.其中正确的结论有(D)‎ ‎ A．0个 B．1个 ‎ C．2个 D．3个 ‎　　　‎ 二、填空题(每小题4分，共20分)[来源:Zxxk.Com]‎ ‎9．在广大农村，为了防止大风吹坏玻璃，大多数人都安装风钩来固定它，这种风钩使用的数学道理是三角形的稳定性．‎ ‎10．请观察图中的5组图案，其中是全等形的是(1)(4)(5)(填序号)．‎ ‎[来源:学科网ZXXK]‎ ‎11．(湖州中考)如图，若△ABC≌△DEF，则∠E为80°．[来源:Zxxk.Com]‎ ‎12．如图，若AB＝AD，∠BAC＝∠DAC，则△ABC≌△ADC，全等的依据是SAS．‎ ‎13．(钦州中考)在△ABC和△BAD中，BC＝AD，请你补充一个条件，使△ABC≌△BAD，你补充的条件是答案不唯一，如：AC＝BD(只填一个)．‎ ‎　　　　‎ 三、解答题(共56分)‎ ‎14．(8分)如图所示，已知△ABD≌△ACD，且B，D，C在同一条直线上，‎ 那么AD与BC是怎样的位置关系？为什么？‎ 解：AD⊥BC.理由：‎ 因为△ABD≌△ACD，‎ 所以∠ADB与∠ADC是对应角．‎ 又因为∠ADB＋∠ADC＝180 °，‎ 所以∠ADB＝∠ADC＝90 °.‎ 所以AD⊥BC.‎ ‎15．(10分)(铜仁中考)如图所示，已知∠1＝∠2，请你添加一个条件，试说明：AB＝AC.‎ ‎(1)你添加的条件是∠B＝∠C；‎ ‎(2)请写出说明过程．‎ 解：在△ABD和△ACD中，‎ ‎∠B＝∠C，∠1＝∠2，AD＝AD，‎ 所以△ABD≌△ACD(AAS)．[来源:学科网ZXXK]‎ 所以AB＝AC.‎ ‎16．(12分)(阜新中考改编)如图，E，F是四边形ABCD的对角线BD上的两点，AE∥CF，AE＝CF，BE＝DF.△ADE与△CBF全等吗？请说明理由．[来源:学.科.网Z.X.X.K]‎ 解：△ADE≌△CBF.理由：因为AE∥CF，‎ 所以∠AED＝∠CFB.‎ 因为DF＝BE，‎ 所以DF＋EF＝BE＋EF，即DE＝BF.‎ 在△ADE和△CBF中，‎ AE＝CF，∠AED＝∠CFB，DE＝BF，[来源:Z|xx|k.Com]‎ 所以△ADE≌△CBF(SAS)．‎ ‎17．(12分)(吉林中考)如图，在△ABC和△DAE中，∠BAC＝∠DAE，AB＝AE，AC ‎＝AD，连接BD，CE，△ABD与△AEC全等吗？请说明理由．‎ 解：△ABD≌△AEC，理由：‎ 因为∠BAC＝∠DAE，‎ 所以∠BAC－∠BAE＝∠DAE－∠BAE，即∠CAE＝∠BAD.‎ 在△ABD和△AEC中，‎ AD＝AC，∠BAD＝∠EAC，AB＝AE，[来源:学科网ZXXK]‎ 所以△ABD≌△AEC(SAS)．‎ ‎18．(14分)如图，在四边形ABCD中，∠ABC＋∠D＝180°，AC平分∠BAD，CE⊥AB，CF⊥AD.试说明：‎ ‎(1)△CBE≌△CDF；‎ ‎(2)AB＋DF＝AF.‎ 解：(1)因为AC平分∠BAD，‎ CE⊥AB，CF⊥AD，AC＝AC，‎ 所以△ACE≌△ACF(AAS)．‎ 所以CE＝CF.‎ 因为∠ABC＋∠D＝180 °，∠ABC＋∠EBC＝180 °，‎ 所以∠EBC＝∠D.‎ 又因为∠CEB＝∠CFD＝90 °，‎ 所以△CBE≌△CDF(AAS)．‎ ‎(2)因为△ACE≌△ACF，所以AE＝AF.‎ 因为△CBE≌△CDF，所以BE＝DF.[来源:学_科_网]‎ 所以AB＋DF＝AB＋BE＝AE＝AF.‎