北师大版七年级上册-第15讲-一元一次方程的应用（培优）-学案

北师大版七年级上册-第15讲-一元一次方程的应用（培优）-学案

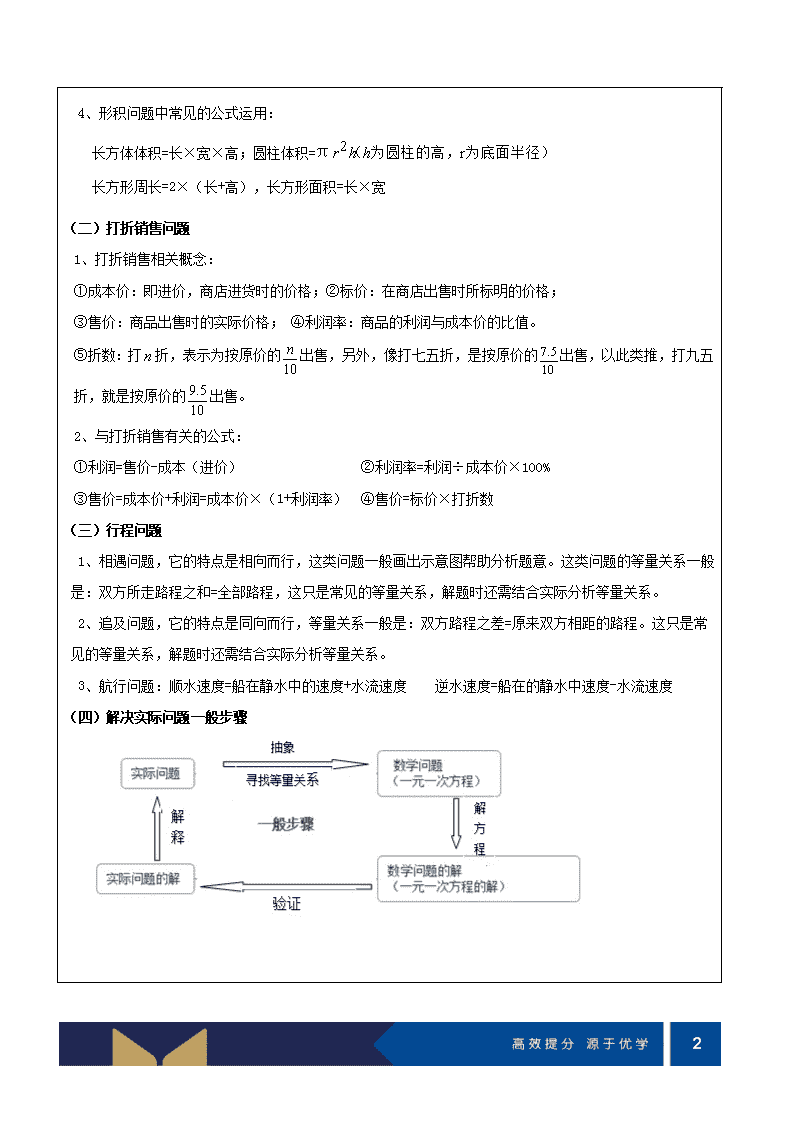
1 学科教师辅导讲义 学员编号： 年 级：七年级 课 时 数：3 学员姓名： 辅导科目：数学 学科教师： 授课主题 第 15 讲 --- 一元一次方程的应用 授课类型 T 同步课堂 P 实战演练 S 归纳总结 教学目标 1 了解一元一次方程应用题的典型例题，以及其中的解题思路 2 熟练提炼应用题等量关系，根据等量关系，设立未知数，列方程求解。 授课日期及时段 T（Textbook-Based）——同步课堂 体系搭建 一、知识框架 二、知识概念 （一）形积变化问题 1、形状发生了变化，而体积没变。此时，等量关系为变化前后体积相等； 2、形状、面积发生了变化，而周长没变。此时，等量关系为变化前后周长相等； 3、形状、体积不同，但根据题意能找出体积之间的关系，把这个关系作为等量关系 2 4、形积问题中常见的公式运用： 长方体体积=长×宽×高；圆柱体积=π 2 rr h h（ 为圆柱的高， 为底面半径） 长方形周长=2×（长+高），长方形面积=长×宽 （二）打折销售问题 1、打折销售相关概念： ①成本价：即进价，商店进货时的价格；②标价：在商店出售时所标明的价格； ③售价：商品出售时的实际价格； ④利润率：商品的利润与成本价的比值。 ⑤折数：打 n 折，表示为按原价的 10 n 出售，另外，像打七五折，是按原价的 7.5 10 出售，以此类推，打九五 折，就是按原价的 9.5 10 出售。 2、与打折销售有关的公式： ①利润=售价-成本（进价） ②利润率=利润÷成本价×100% ③售价=成本价+利润=成本价×（1+利润率） ④售价=标价×打折数 （三）行程问题 1、相遇问题，它的特点是相向而行，这类问题一般画出示意图帮助分析题意。这类问题的等量关系一般 是：双方所走路程之和=全部路程，这只是常见的等量关系，解题时还需结合实际分析等量关系。 2、追及问题，它的特点是同向而行，等量关系一般是：双方路程之差=原来双方相距的路程。这只是常 见的等量关系，解题时还需结合实际分析等量关系。 3、航行问题：顺水速度=船在静水中的速度+水流速度 逆水速度=船在的静水中速度-水流速度 （四）解决实际问题一般步骤 3 典例分析 考点一： 形积问题 例 1、用直径为 90mm 的圆柱形玻璃杯（已装满水，且水足够多）向一个内底面积为 131×131mm2，内高 为 81mm 的长方体铁盒倒水，当铁盒装满水时，玻璃杯中水的高度下降了多少？（结果保留π） 例 2、准备两张同样大小的正方形纸片 （1）取准备好的一张正方形纸片，将它的四周各剪去一个同样大小的正方形（如图），再折合成一个无盖 的长方体盒子．做成的长方体盒子的底面的边长为 6cm，容积为 108cm3，那么原正方形纸片的边长为多少？ （2）取准备好的另一张正方形纸片，这张纸片恰好可做成圆柱形食品罐侧面的包装纸（不计接口部分）， 这个食品罐的体积是多少？（结果保留π） 例 3、用直径为 120mm 的圆钢铸造成 5.9kg 工件，每立方厘米的圆钢重 7.8g，这样需截取圆钢的长是多少 mm？解题时，设需要截面圆钢的长为 xmm，那么下面列方程正确的是（ ） A．7.8×1202•π•x=5.9 B． C． D． 4 考点二： 打折销售问题 例 1、在某市场，甲、乙两人各销售 100 件某种衬衫，甲本着薄利多销的原则，不久全部售完；乙最初售价 每件比甲贵 18 元，卖出一半后因十分滞销，不得已按最初销售价对折销售，虽勉强售完，但多花了时间， 且最后卖得的总钱数比甲所得少 10%，求甲每件衬衫的售价 例 2、某公司生产一种产品，每件产品成本价是 400 元，销售价为 510 元，第一季度销售了 5000 件． （1）求该产品第一季度的销售总利润（销售利润=销售价﹣成本价）是多少元？ （2）为进一步扩大市场，公司决定降低生产成本，经过市场凋研，在降低生产成本后，第二季度这种产品 每件销售价降低了 4%，销售量比第一季度提高了 10%，销售总利润比第一季度提高了 20%．求该产品每件 的成本价降低了多少元？ 例 3、某商场因换季，将一品牌服装打折销售，每件服装如果按标价的六折出售将亏 10 元，而按标价的七 五折出售将赚 50 元，问： （1）每件服装的标价是多少元？ （2）每件服装的成本是多少元？ （3）为保证不亏本，最多能打几折？ 5 考点三：行程问题 例 1、如图所示，甲、乙两人在环形跑道上练习跑步，已知环形跑道一圈长 400 米，乙 每秒钟跑 6 米，甲的速度是乙的 倍 （1）如果甲、乙在跑道上相距 8 米处同时反向出发，那么经过多少秒两人首次相遇？ （2）如果甲在乙前面 8 米处同时同向出发，那么经过多少秒两人首次相遇？ 例 2、一列火车匀速行驶，经过一条长 300m 的隧道需要 20s 的时间，隧道的顶上有一盏灯，垂直向下发光， 灯光照在火车上的时间是 10s，根据以上数据，你能否求出火车的长度？若能，火车的长度是多少？若不能， 请说明理由 例 3、A、B 两地相距 400km，甲、乙两车分别从 A、B 两地同时出发，相向而行，甲车以每小时 100km 速 度匀速行驶 1h 后，休息了 1h，然后按原速继续行驶到 B 地，乙车以每小时 80km 的速度匀速行驶到 A 地 （1）当乙车经过甲车休息的地方时，乙车行驶的时间是 h； （2）当甲、乙两车相遇时，求乙车行驶的时间； （3）当甲、乙两车相距 40km 时，求乙车行驶的时间 网版权所 有 考点四、解决实际问题 6 例 1、学校准备组织教师和优秀学生参加夏令营，其中教师 22 名，现有甲、乙两家旅行社，两家全票价都 是 200 元，但优惠方式不同：甲旅行社表示教师免费，学生按八折收费； 乙旅行社表示教师和学生一律按 七五折收费 （1）当参加夏令营的学生人数为 x 人时，请你用含 x 的式子分别表示甲、乙旅行社的收费标准． （2）学校领导经过核算后认为甲、乙旅行社的收费一样，请你算出有多少名学生参加夏令营． 例 2、某市自 2015 年 1 月 1 日起对居民生活用电实行阶梯电价，具体收费标准如下表： 一户居民一个月的用电量 电价（元/度） 第 1 档 不超过 240 度的部分 a 第 2 档 超过 240 度但不超过 400 度的部分 0.65 第 3 档 超过 400 度的部分 a+0.3 已知 2016 年 10 月份该市居民老李家用电 200 度，交电费 120 元；2016 年 9 月份老李家交电费 157 元． （1）表中 a 的值为 ； （2）求老李家 2016 年 9 月份的用电量； （3）若 2016 年 8 月份老李家用电的平均电价为 0.7 元/度，求老李家 2016 年 8 月份的用电量 网版权所 有 例 3、某开发公司要生产若干件新产品，需要精加工后，才能投放市场，现有红星和巨星两个加工厂都想加 工这批产品，已知红星厂单独加工这批产品比巨星厂单独加工这批产品多用 20 天，红星厂每天可加工 16 7 件产品，巨星厂每天可加工 24 件产品公司每天需付红星厂每天加工费 80 元，巨星厂每天加工费 120 元． （1）这个公司要加工多少件新产品？ （2）在加工过程中，公司需另派一名工程师每天到厂家进行技术指导，并负担每天 5 元的午餐补助费，公 司制定产品加工方案如下：可由一个厂单独加工完成，也可由两厂合作同时完成，请你帮助公司从所有可 供选择的方案中选择一种即省钱，又省时间的加工方案 P(Practice-Oriented)——实战演练 实战演练  课堂狙击 1、用一根直径为 10 厘米的圆柱形铁柱铸造 12 只直径为 10 厘米的铅球，问应截取多长的铁柱？（球的体 积 V= ） 2、实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为 1：2：1，用两个 相同的管子在容器的 5cm 高度处连通（即管子底端离容器底 5cm），现三个容器中，只有甲中有水，水位高 8 1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水 1 分钟，乙的水位上升 cm， （1）开始注水 1 分钟，丙的水位上升 cm． （2）求出开始注入多少分钟的水量后，甲与乙的水位高度之差是 0.5cm？ 菁优网版 权所有 3、某品牌服装折扣店将某件衣服按进价提高 50%后标价，再打 8 折（标价的 80%）销售，售价为 240 元．设 这件衣服的进价为 x 元，根据题意，所列的方程应为 4、某商场在元旦期间，开展商品促销活动．将某型号的电视机按进价提高 35%后，打 9 折另送 50 元路费 的方式销售，结果每台电视机仍获利 208 元，问每台电视机的进价是多少元？ 5、某校七年级社会实践小组去某商场调查商品的销售情况，了解到该商场以每件 80 元的价格购进了某品 牌衬衫 500 件，并以每件 120 元的价格销售了 400 件，商场准备采取促销措施，将剩下的衬衫降价销售 （1）每件衬衫降价多少元时，销售完这批衬衫正好达到盈利 45%的预期目标？ 9 （2）某公司给员工发福利，在该商场促销钱购买了 20 件该品牌的衬衫发给员工，后因为有新员工加入， 又要购买 5 件该衬衫，购买这 5 件衬衫时恰好赶上该商场进行促销活动，求该公司购买这 25 件衬衫的平均 价格 6、A、B 两列火车长分别是 120m 和 144m，A 车比 B 车每秒多行 5m （1）两列相向行驶，从相遇到两车全部错开需 8 秒，问两车的速度各是多少？ （2）在（1）的条件下，若同向行驶，A 车的车头从 B 车的车尾追及到 A 车全部超出 B 车，需要多少秒？ 7、A、B 两地相距 64 千米，甲从 A 地出发，每小时行 14 千米，乙从 B 地出发，每小时行 18 千米 （1）若两人同时出发相向而行，则需经过几小时两人相遇？ （2）若两人同时出发相向而行，则需几小时两人相距 16 千米？ （3）若甲在前，乙在后，两人同时同向而行，则几小时后乙超过甲 10 千米？ 8、只列方程，不解方程：一队战士用 4km/h 的速度行军训练，在队尾的通讯员以 6km/h 的速度跑至队首将 命令传给队长，然后立即按原速度赶回队尾，共用 7.2min，求这列队伍的长（传令时间不计） 10 9、2016 年春节即将来临，甲、乙两单位准备组织退休职工到某风景区游玩．甲、乙两单位共 102 人，其中 甲单位人数多于乙单位人数，且甲单位人数不够 100 人．经了解，该风景区的门票价格如下表： 数量（张） 1﹣50 51﹣100 101 张及以上 单价（元/张） 60 元 50 元 40 元 如果两单位分别单独购买门票，一共应付 5500 元． （1）如果甲、乙两单位联合起来购买门票，那么比各自购买门票共可以节省多少钱？ （2）甲、乙两单位各有多少名退休职工准备参加游玩？ （3）如果甲单位有 12 名退休职工因身体原因不能外出游玩，那么你有几种购买方案，通过比较，你该如 何购买门票才能最省钱？菁优网版 权所有  课后反击 1、将 50 个底面半径为 4cm，高为 20cm 的圆柱形铁料熔化后浇铸成长方体，且长方体底面是边长为 4cm 的 正方形，长方体的高为 10cm．已知熔化、浇铸过程中，材料会有 1.8%的损耗，问最终能铸得多少个上述长 11 方体？（π取 3.14） 2、某水果零售商店在杨梅销售季节分两批次从批发市场共购进杨梅 60 箱，已知第一、二次进货价分别为 每箱 50 元、40 元，且第二次比第一次多付款 600 元 （1）求第一、二次各购进杨梅多少箱； （2）若商店对这 60 箱杨梅先按每箱 60 元销售了 25 箱，其余的每箱打八折销售完．求商店销售完全部杨 梅所获得的利润．（注：按整箱出售，利润=销售总收人﹣进货总成本） 菁优网版 权所有 3、某商店在某一时间以毎件 100 元的价格卖出兩件衣服，其中一件盈利 25%，另一件亏损 20%，求该商店 卖出这两件衣服的盈亏情况 4、某船从 A 港顺流而下到达 B 港口，然后逆流返回，在到达 A、B 间的 C 港口时，一共航行了 7 小时， 已知此船在静水中的速度为 8 千米/小时，水流速度为 2 千米/小时，A、C 两港口相距 6 千米，求 A、B 两 港口间的距离 12 5、一次远足活动中，一部分人步行，另一部分乘一辆汽车，两部分人同地出发．步行者比汽车提前半小时 出发，这辆汽车到达目的地后，再回头接步行这部分人．出发地到目的地的距离是 50 公里．问：步行者在 出发后经多少时间与回头接他们的汽车相遇（汽车掉头的时间忽略不计）？ 6、某家具店出售桌子和椅子，单价分别为 300 元一张和 60 元一把，该家具店制定了两种优惠方案： （1）买一张桌子送两把椅子； （2）按总价的 87.5%付款．某单位购买 5 张桌子和若干把椅子（不少于 10 把），如果已知要购买 x 把椅子， 讨论该单位购买同样多的椅子时，选择哪一种方案更省钱？ 7、某服装厂生产一批西装，每 2 米宽面布可以裁上衣 3 件或裁裤子 4 条，现有宽面布 245 米，为了使上衣 和裤子配套，裁上衣和裤子应该各用宽面布多少米？ 13 直击中考 1、【2015 深圳】下表为深圳市居民每月用水收费标准，（单位：元/m3）。 用水量 单价 22x a 剩余部分 1.1a （1）某用户用水 10 立方米，公交水费 23 元，求 a 的值； （2）在（1）的前提下，该用户 5 月份交水费 71 元，请问该用户用水多少立方米？ 2、【2012 梧州】今年 5 月，在中国武汉举办了汤姆斯杯羽毛球团体赛．在 27 日的决赛中，中国队占胜韩 国队夺得了冠军．某羽毛球协会组织一些会员到现场观看了该场比赛．已知该协会购买了每张 300 元和每 张 400 元的两种门票共 8 张，总费用为 2700 元．请问该协会购买了这两种门票各多少张？ S(Summary-Embedded)——归纳总结 重点回顾 一、打折销售问题 1、打折销售相关概念： ①成本价：即进价，商店进货时的价格；②标价：在商店出售时所标明的价格； 14 ③售价：商品出售时的实际价格； ④利润率：商品的利润与成本价的比值。 ⑤折数：打 n 折，表示为按原价的 10 n 出售，另外，像打七五折，是按原价的 7.5 10 出售，以此类推，打九五 折，就是按原价的 9.5 10 出售。 2、与打折销售有关的公式： ①利润=售价-成本（进价） ②利润率=利润÷成本价×100% ③售价=成本价+利润=成本价×（1+利润率） ④售价=标价×打折数 二、行程问题 1、相遇问题，它的特点是相向而行，这类问题一般画出示意图帮助分析题意。这类问题的等量关系一般 是：双方所走路程之和=全部路程，这只是常见的等量关系，解题时还需结合实际分析等量关系。 2、追及问题，它的特点是同向而行，等量关系一般是：双方路程之差=原来双方相距的路程。这只是常 见的等量关系，解题时还需结合实际分析等量关系。 3、航行问题：顺水速度=船在静水中的速度+水流速度 逆水速度=船在的静水中速度-水流速度 名师点拨 1、解决实际问题一般步骤 学霸经验  本节课我学到了  我需要努力的地方是 15