不等式的性质教案

不等式的性质教案

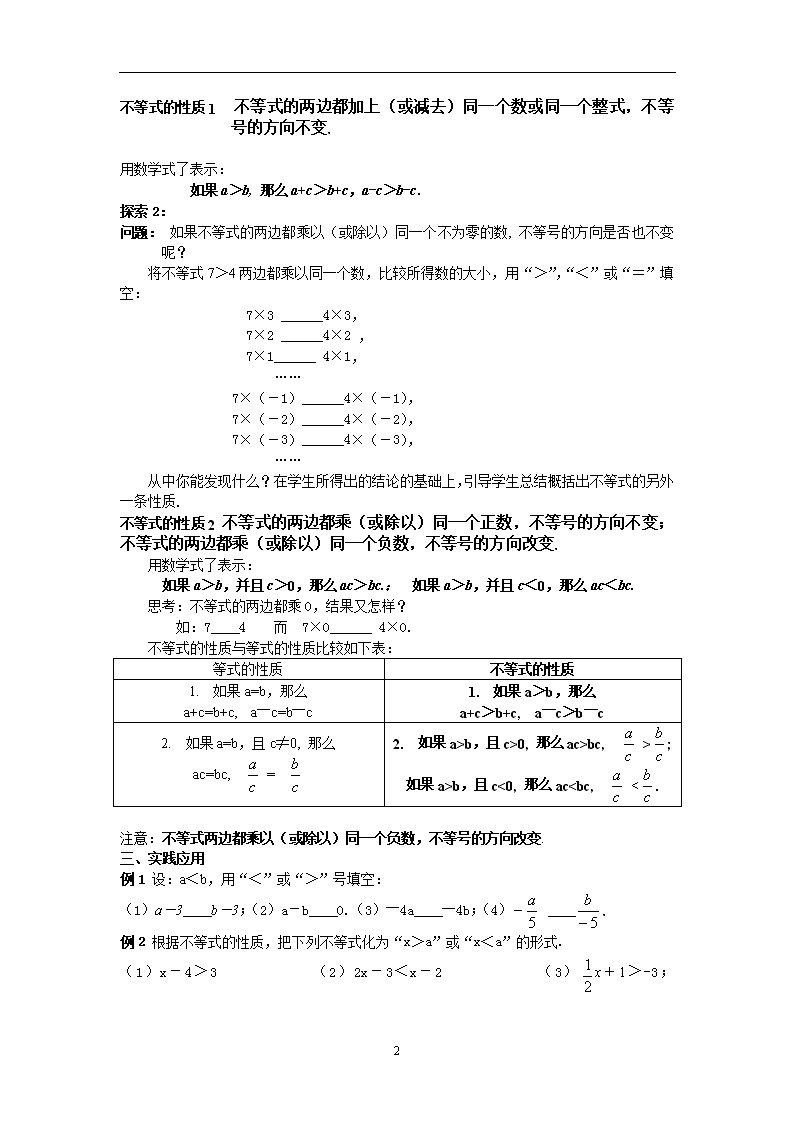
‎ ‎ ‎11.3不等式的性质 目标要求：‎ ‎1．掌握不等式的两条基本性质，并能熟练的应用不等式的性质进行不等式的变形；‎ ‎2．理解不等式的基本性质与等式的基本性质之间的区别.‎ 过程性目标 在积极参与探索、发现不等式基本性质的过程中，体会不等式的两条基本性质的作用和意义，培养学生探索数学问题的能力.‎ 情感态度目标 ‎1．通过学生的自主讨论培养学生的观察力和归纳的能力；‎ ‎2．通过学生的讨论使学生进一步体会集体的作用，培养其集体合作的精神.‎ 重点和难点 重点：掌握不等式的两条基本性质，尤其是不等式的基本性质2；‎ 难点：正确应用不等式的两条基本性质进行不等式的变形.‎ 一、 创设情境 问：在解一元一次方程时，我们主要是对方程进行变形，那么方程变形主要有哪些？‎ 答：去分母、移项、系数化为1.‎ 问：这些解法具体步骤的主要依据是等式的两条基本性质.‎ 等式基本性质1：在等式的两边都加上（或减去）同一个数或同一个整式，所得的结果仍是等式；‎ 等式基本性质2：等式的两边都乘以或除以同一个数不等于0的数，所得的结果仍是等式 探索1：‎ ‎（1）请同学们观察：课本P.12电梯里两人身高分别为：a米、b米，且a＞b，都升高6米后的高度后的不等式关系：a＋6＞b＋6；同理：a－3　　b－3（填写“＜”、“＞”号 ‎（2）实物演示：一个倾斜的天平两边分别放有重物，其质量分别为a和b（显然有a＞b）,如果在两边盘内再分别加上等量的砝码c，那么盘子会出现什么情况？‎ 可让学生进行操作，并得出结论：盘子仍然像原来那样倾斜（即a+c＞b+c）.‎ ‎ ‎ ‎ a＞b a+c＞b+c.‎ ‎　　‎ 归纳1:‎ 教师在学生得出结论的前提下总结：‎ 4‎ ‎ ‎ 不等式的性质1 　不等式的两边都加上（或减去）同一个数或同一个整式，不等号的方向不变.‎ 用数学式了表示：‎ 如果a＞b, 那么a+c＞b+c，a-c＞b-c.‎ 探索2：‎ 问题： 如果不等式的两边都乘以（或除以）同一个不为零的数, 不等号的方向是否也不变呢？‎ 将不等式7＞4两边都乘以同一个数，比较所得数的大小，用“＞”，“＜”或“＝”填空：‎ ‎　　　　　　　　　7×3 ______4×3，‎ ‎7×2 ______4×2 ，‎ ‎7×1______ 4×1，‎ ‎……‎ ‎7×（－1）______4×（－1），‎ ‎7×（－2）______4×（－2），‎ ‎7×（－3）______4×（－3），‎ ‎……‎ 从中你能发现什么？在学生所得出的结论的基础上，引导学生总结概括出不等式的另外一条性质.‎ 不等式的性质2 不等式的两边都乘（或除以）同一个正数，不等号的方向不变；不等式的两边都乘（或除以）同一个负数，不等号的方向改变.‎ 用数学式了表示：‎ 如果a＞b，并且c＞0，那么ac＞bc.； 如果a＞b，并且c＜0，那么ac＜bc.‎ 思考：不等式的两边都乘0，结果又怎样？　　‎ 如：7　　4　　而　7×0______ 4×0.‎ 不等式的性质与等式的性质比较如下表：‎ 等式的性质 不等式的性质 ‎1.　如果a=b，那么 a+c=b+c, a―c=b―c ‎1.　如果a＞b，那么 a+c＞b+c, a―c＞b―c ‎2.　如果a=b，且c≠0, 那么 ac=bc, =‎ 2. 如果a>b，且c>0, 那么ac>bc, >;‎ 如果a>b，且c<0, 那么ac

查看更多