- 2021-10-25 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版七年级上册数学期中测试题(含答案)
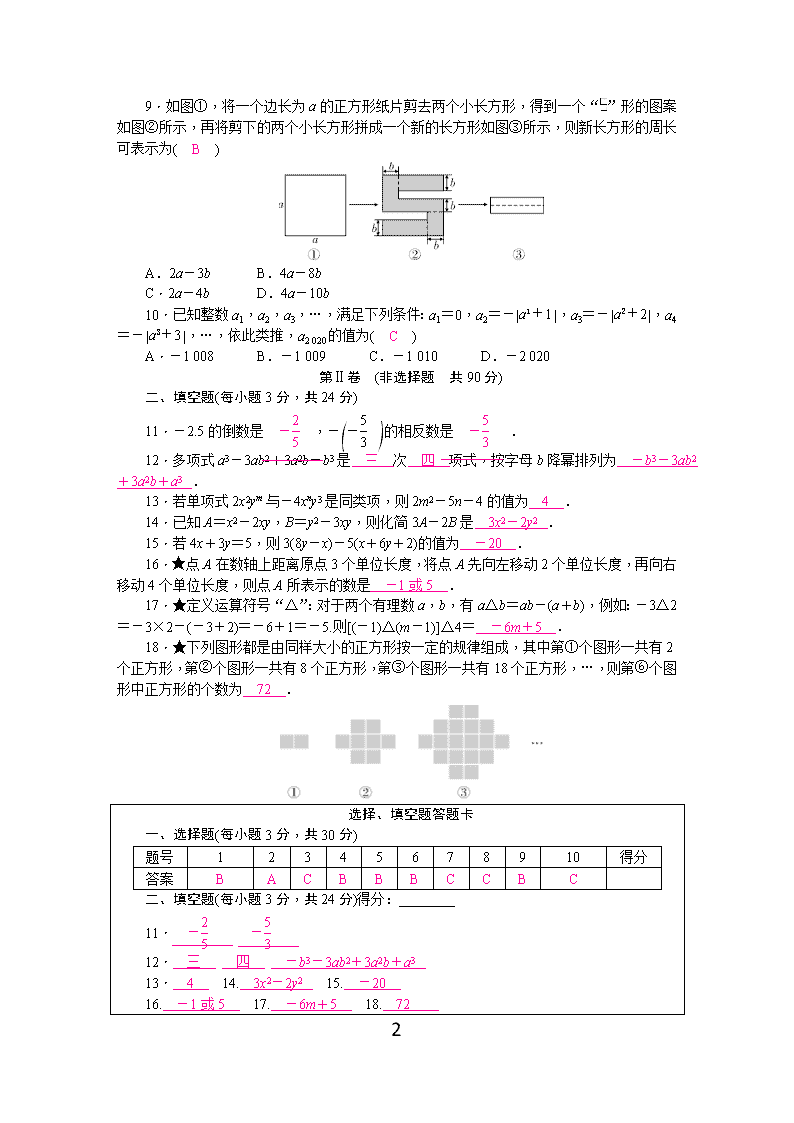
人教版七年级上册数学期中测试题(含答案) (考试时间:120分钟 满分:120分) 分数:____________ 5 第Ⅰ卷 (选择题 共30分) 一、选择题(每小题3分,共30分) 1.当A地高于海平面150米时,记作“+150米,”那么B地低于海平面25米时,记作( B ) A.+25米 B.-25米 C.+175 D.+125米 2.四个数-3,0,1,2中的负数是( A ) A.-3 B.0 C.1 D.2 3.由四舍五入法得到近似数4.6×103,下列说法中正确的是( C ) A.精确到十分位 B.精确到个位 C.精确到百位 D.精确到千位 4.下列说法中正确的是( B ) A.x+y是一次一项式 B.x的系数和次数都是1 C.多项式2πa3+a2-1的次数是4 D.单项式3×103y2的系数是3 5.国产动画电影《哪吒之魔童降世》最终票房收入将近50亿元人民币.50亿用科学记数法表示为( B ) A.50×108 B.5×109 C.5×1010 D.0.5×1010 6.数轴上A,B,C三点表示的有理数分别为a,b,c,若ab<0,a+b>0,a+b+c<0,则下列数轴符合题意的是( B ) A. B. C. D. 7.在数学课上,老师让甲、乙、丙、丁四位同学分别做了一道有理数运算题,你认为做对的同学是( C ) 甲:9-32÷8=0÷8=0; 乙:24-(4×32)=24-4×6=0; 丙:(36-12)÷=36×-12×=16; 丁:(-3)2÷×3=9÷1=9. A.甲 B.乙 C.丙 D.丁 8.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.-=-x2+y2,阴影部分即为被墨水弄污的部分.那么被墨水遮住的一项应是( C ) A.-7xy B.+7xy C.-xy D.+xy 5 9.如图①,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”形的图案如图②所示,再将剪下的两个小长方形拼成一个新的长方形如图③所示,则新长方形的周长可表示为( B ) A.2a-3b B.4a-8b C.2a-4b D.4a-10b 10.已知整数a1,a2,a3,…,满足下列条件:a1=0,a2=-,a3=-,a4=-,…,依此类推,a2 020的值为( C ) A.-1 008 B.-1 009 C.-1 010 D.-2 020 第Ⅱ卷 (非选择题 共90分) 二、填空题(每小题3分,共24分) 11.-2.5的倒数是 - ,-的相反数是 - . 12.多项式a3-3ab2+3a2b-b3是 三 次 四 项式,按字母b降幂排列为 -b3-3ab2+3a2b+a3 . 13.若单项式2x2ym与-4xny3是同类项,则2m2-5n-4的值为 4 . 14.已知A=x2-2xy,B=y2-3xy,则化简3A-2B是 3x2-2y2 . 15.若4x+3y=5,则3(8y-x)-5(x+6y+2)的值为 -20 . 16.★点A在数轴上距离原点3个单位长度,将点A先向左移动2个单位长度,再向右移动4个单位长度,则点A所表示的数是 -1或5 . 17.★定义运算符号“△”:对于两个有理数a,b,有a△b=ab-(a+b),例如:-3△2=-3×2-(-3+2)=-6+1=-5.则[(-1)△(m-1)]△4= -6m+5 . 18.★下列图形都是由同样大小的正方形按一定的规律组成,其中第①个图形一共有2个正方形,第②个图形一共有8个正方形,第③个图形一共有18个正方形,…,则第⑥个图形中正方形的个数为 72 . 选择、填空题答题卡 一、选择题(每小题3分,共30分) 题号 1 2 3 4 5 6 7 8 9 10 得分 答案 B A C B B B C C B C 二、填空题(每小题3分,共24分)得分:________ 11. - - 12. 三 四 -b3-3ab2+3a2b+a3 13. 4 14. 3x2-2y2 15. -20 16. -1或5 17. -6m+5 18. 72 5 三、解答题(共66分) 19.(8分)填空. 9,-,+4.3,,-(+7),18%,(-13)4,-6,0. 正分数:{+4.3,,18%,…}; 负分数:; 整数:{9,-(+7),(-13)4,-6,0,…}; 非负整数:{9,(-13)4,0,…}. 20.(9分)计算: (1)-10+8÷(-2)3-(-40)×(-3)+(-1)2 020; 解:原式=-10+8÷(-8)-120+1 =-10-1-120+1 =-130. (2)÷-×-÷4; 解:原式=×--× =--- =-. (3)÷. 解:原式=÷ =[30-(28+30-33)]×(-5) =5×(-5) =-25. 21.(8分)化简: (1)3x2+2x+1-2(x2+x-1); 解:原式=3x2+2x+1-2x2-2x+2 =x2+3. (2)(-4ab+3a)-3(a-b)-2(a2-2ab). 解:原式=-4ab+3a-3a+3b-2a2+4ab =3b-2a2. 22.(10分)先化简,再求值: (1)-a2b+(3ab2-a2b)-2(2ab2-a2b),其中a=-1,b=-2; 解:原式=-a2b+3ab2-a2b-4ab2+2a2b =-ab2. 当a=-1,b=-2时, 原式=-(-1)×(-2)2=1×4=4. (2)2x2--2(x2-xy+2y2),其中x=,y=-1. 5 解:原式=2x2-(-x2+2xy-2y2)-2(x2-xy+2y2) =2x2+x2-2xy+2y2-2x2+2xy-4y2 =x2-2y2, 当x=,y=-1时,原式=-2=-. 23.(10分)如图是某市设计的长方形休闲广场,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池. (1)用图中所标字母表示广场空地(图中阴影部分)的面积; (2)若休闲广场的长为80米,宽为40米,求广场空地的面积(计算结果保留π). 解:(1)广场空地的面积为xy-π-π =xy-π x2. (2)当x=40,y=80时, 广场空地的面积为 40×80-π×402=3 200-500π(平方米). 24.(9分)如图,将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中左上角的一个小正方形按同样的方法剪成四个小正方形,再将其中左上角的一个小正方形按同样的方法剪成四个小正方形,如此循环进行下去. (1)填表: 剪的次数 1 2 3 4 5 正方形的个数 4 7 10 13 (2)如果剪了100次,那么共剪出多少个小正方形? (3)如果剪n次,那么共剪出多少个小正方形? (4)如果要剪出100个小正方形,那么需要剪多少次? 解:(1)填表如下: 剪的次数 1 2 3 4 5 正方形的个数 4 7 10 13 16 (2)结合题中图形,不难发现正方形的个数在4的基础上依次加3. 4+3×(100-1)=301, 所以如果剪了100次,那么共剪出301个小正方形. (3)如果剪了n次,那么共剪出(3n+1)个小正方形. (4)令3n+1=100,解得n=33. 5 答:如果要剪出100个小正方形,那么需要剪33次. 25.(12分)【阅读理解】的几何意义是数轴上表示数a的点与原点的距离,那么可以看作是数轴上表示数a的点与表示1的点的距离,+可以看作是数轴上表示数a的点与表示1和2两个点的距离之和.下面我们结合数轴研究+的最小值,我们先看a的三种可能情况:如图,①a<1;②1≤a≤2;③a>2. ,①) ,②) ,③) 由图可以看出,当a<1时,+>1;当1≤a≤2时,+=1;当a>2时,+>1. 那么我们可以得到当1≤a≤2时,+有最小值的结论. 【问题解决】 (1)++的几何意义是________________; (2)++的最小值是________,并在如图所示的数轴上描出得到最小值时a所在的位置. 【深入探究】通过材料的阅读和问题的解决,你现在对求+++…的最小值问题有所了解吗?在数轴上找到表示数a的点的位置可以帮助我们顺利解决问题,下面请你结合数轴算一算++++的最小值; (3)求+++…+的最小值. 解:(1)数轴上表示数a的点与表示1,2,3三个点的距离之和. (2)2;如图所示: 【深入探究】根据题意,得当a=3时,++++取得最小值,最小值为2+1+0+1+2=6. (3)根据题意,得当a=1 010时,+++…+取得最小值,最小值为1 009+1 008+1 007+…+1+0+1+…+1 009=1 009×(1 009+1)=1 019 090. 5查看更多