- 2021-10-25 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
平移的特征教案1
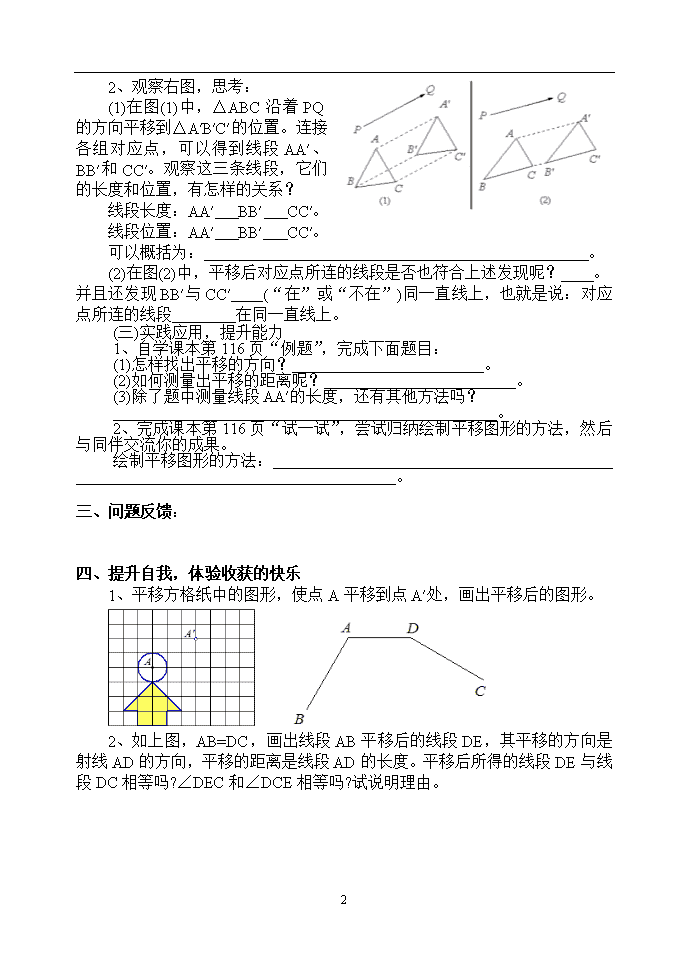
10.2.2平移的特征 一、学习目标: 1、理解并掌握平移的特征,能根据已知条件画出平移后的图形。 2、经历将复杂图形的平移转化为简单图形的平移的过程,进一步体会数学学习中“转化”思想的重要性;探索平移的特征,体验几何学习研究中的常用方法。 3、鼓励学生积极参与各种教学环节,并从中获得成就感,获得数学的活动经验;培养学生能和谐、流利的与人交流、探讨数学问题的良好的心理素质。 二、依据问题自主探究,体验独立解决问题的乐趣 (一)设置情景,引入新课 1、观察上面图片,并思考回答下面的问题: (1)三幅图“火箭升空”、“飞行表演”和“乘坐电梯”中,火箭、飞机和乘客的位置有怎样的变化呢? (2)三幅图中物体的位置变换,属于我们学过的哪一种图形变换? 2、平移的要素是什么? 。 3、根据右图,完成习题: 如图,当我们使用直尺和三角尺画平行线时,△ABC沿着直尺PQ平移到了△A′B′C′的位置。请你说出对应点、对应角和对应线段,以及平移的方向和平移的距离。 (二)学习新知,探究归纳 1、继续观察上面第3题图,思考: (1)图中的各组对应线段的长度和位置有怎样的关系? 我们可以发现:A′B′∥AB,A′B′=AB。 同时也有A′C′∥ ,A′C′= ;B′C′∥ ,B′C′= 。 可以概括为: 。 (2)图中的各组对应角的大小有怎样的关系? 我们可以发现:∠B′=∠B。 同时也有∠C′=∠ ,∠A′=∠ 。 可以概括为: 。 (3)平移后的图形与原来的图形的形状与大小有没有发生变化? 。 2 2、观察右图,思考: (1)在图(1)中,△ABC沿着PQ的方向平移到△A′B′C′的位置。连接各组对应点,可以得到线段AA′、BB′和CC′。观察这三条线段,它们的长度和位置,有怎样的关系? 线段长度:AA′ BB′ CC′。 线段位置:AA′ BB′ CC′。 可以概括为: 。 (2)在图(2)中,平移后对应点所连的线段是否也符合上述发现呢? 。 并且还发现BB′与CC′ (“在”或“不在”)同一直线上,也就是说:对应点所连的线段 在同一直线上。 (三)实践应用,提升能力 1、自学课本第116页“例题”,完成下面题目: (1)怎样找出平移的方向? 。 (2)如何测量出平移的距离呢? 。 (3)除了题中测量线段AA′的长度,还有其他方法吗? 。 2、完成课本第116页“试一试”,尝试归纳绘制平移图形的方法,然后与同伴交流你的成果。 绘制平移图形的方法: 。 三、问题反馈: 四、提升自我,体验收获的快乐 1、平移方格纸中的图形,使点A平移到点A′处,画出平移后的图形。 2、如上图,AB=DC,画出线段AB平移后的线段DE,其平移的方向是射线AD的方向,平移的距离是线段AD的长度。平移后所得的线段DE与线段DC相等吗?∠DEC和∠DCE相等吗?试说明理由。 2查看更多