- 2021-10-22 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
探索平行线的性质教案
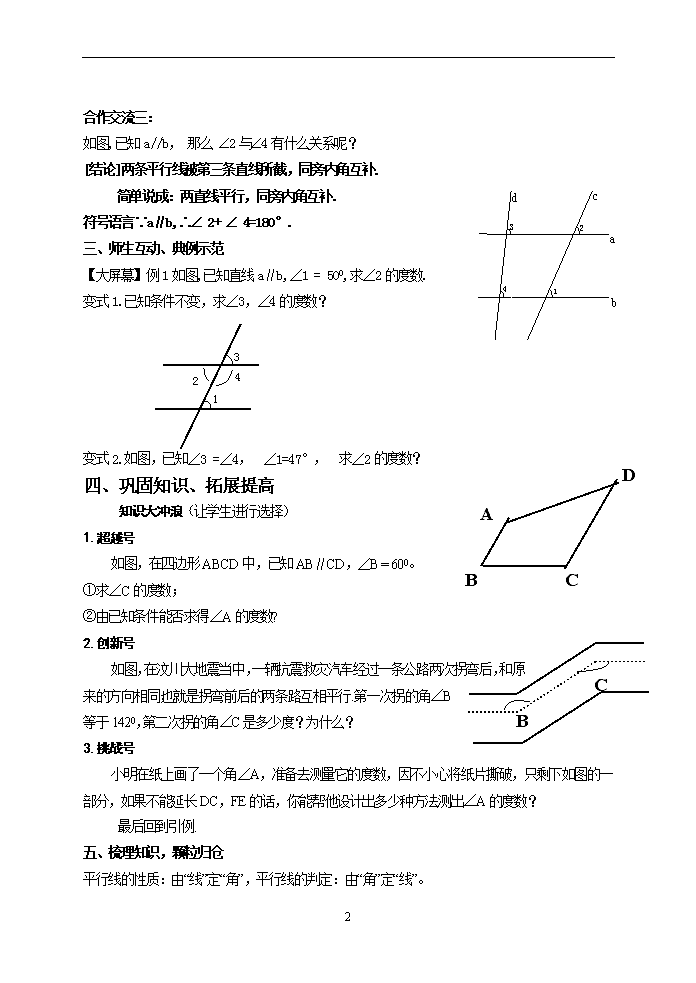
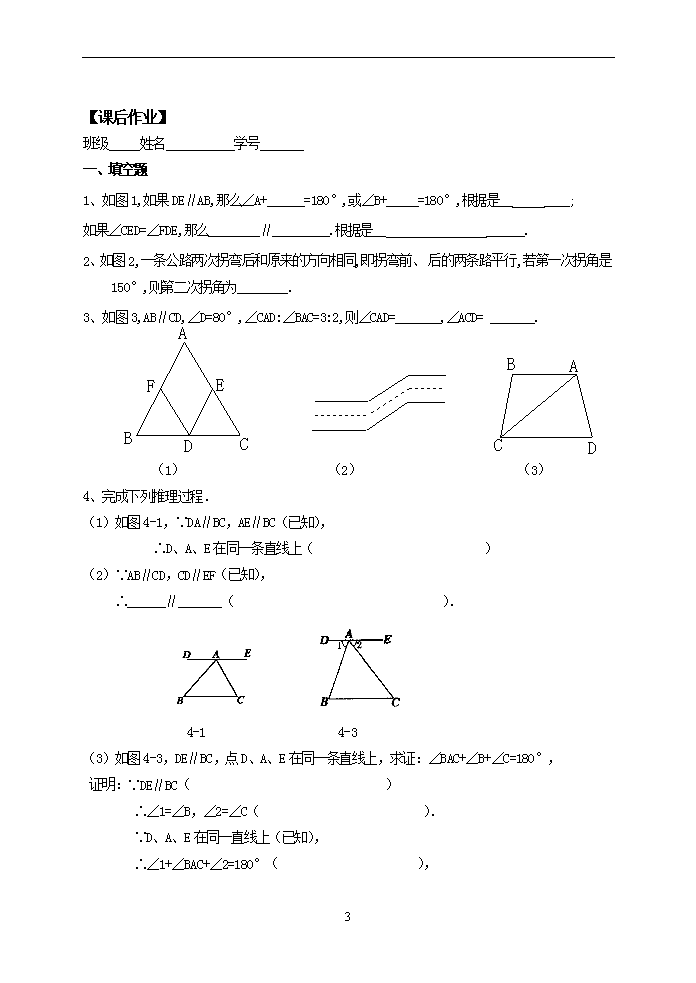
7.2 探索平行线的性质 学习目标 1.掌握平行线的三个特征(即性质定理),并能解决一些问题. 2.理解平行线的判定与性质的区别与应用 学习难点 平行线性质的运用 教学过程 一、情境引入 1.引入课题 如右图,世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成塔高54.5米. 目前,它与地面所成的较小的角为85º,它与地面所成的较大的角是多少度? 由此得出本节课题:平行线的性质 2.复习回顾 平行线的判定方法有哪些?反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢? 二、交流合作、探索发现 合作交流一: 看课本第11图7—10。猜一猜∠1和∠2相等吗?还有别的方法吗? 图中还有其它同位角吗?它们的大小有什么关系? 是不是任意一条直线去截平行线a、b所得的同位角都相等呢? 1 3 2 [结论] 两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等. 符号语言:∵a∥b,∴∠1=∠2. 4 1 2 合作交流二: 如图:已知a//b,那么Ð2与Ð 3相等吗?为什么? [结论]两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等. 符号语言:∵a∥b,∴∠2=∠3. 4 合作交流三: 如图,已知a//b, 那么 Ð2与Ð4有什么关系呢? [结论]两条平行线被第三条直线所截,同旁内角互补. 简单说成:两直线平行,同旁内角互补. 符号语言∵a∥b,∴Ð 2+ Ð 4=180°. 三、师生互动、典例示范 【大屏幕】例1如图,已知直线a∥b,∠1 = 500,求∠2的度数. 变式1.已知条件不变,求∠3,∠4的度数? 1 3 2 4 B A D C 变式2.如图,已知∠3 =∠4, ∠1=47°, 求∠2的度数? 四、巩固知识、拓展提高 知识大冲浪(让学生进行选择) 1.超越号 如图,在四边形ABCD中,已知AB∥CD,∠B = 600。 ①求∠C的度数; ②由已知条件能否求得∠A的度数? B C 2.创新号 如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么? 3.挑战号 小明在纸上画了一个角∠A,准备去测量它的度数,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC,FE的话,你能帮他设计出多少种方法测出∠A的度数? 最后回到引例. 五、梳理知识,颗粒归仓 平行线的性质:由“线”定“角”,平行线的判定:由“角”定“线”。 4 【课后作业】 班级 姓名 学号 一、填空题 1、如图1,如果DE∥AB,那么∠A+______=180°,或∠B+_____=180°,根据是 __ ____; 如果∠CED=∠FDE,那么________∥_________.根据是__ ______. 2、如图2,一条公路两次拐弯后和原来的方向相同,即拐弯前、后的两条路 平行,若第一次拐角是150°,则第二次拐角为________. 3、如图3,AB∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______,∠ACD=_______. (1) (2) (3) 4、完成下列推理过程. (1)如图4-1,∵DA∥BC,AE∥BC(已知), ∴D、A、E在同一条直线上( ) (2)∵AB∥CD,CD∥EF(已知), ∴______∥_______( ). 4-1 4-3 (3)如图4-3,DE∥BC,点D、A、E在同一条直线上,求证:∠BAC+∠B+∠C=180°, 证明:∵DE∥BC( ) ∴∠1=∠B,∠2=∠C( ). ∵D、A、E在同一直线上(已知), ∴∠1+∠BAC+∠2=180°( ), 4 ∴∠BAC+∠B+∠C=180°( ). 二、选择题 5、下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内 错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是 ( ) A.① B.②和③ C.④ D.①和④ 6、如图1,AB∥CD,AD,BC相交于O,∠BAD=35°,∠BOD=76°,则∠C的度数是( ) A.31° B.35° C.41° D.76° 7、如图2,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(∠1除外)共有 ( ) A.6个 B.5个 C.4个 D.3个 8、如图3,在平行四边形ABCD中,下列各式不一定正确的是 ( ) A.∠1+∠2=180° B.∠2+∠3=180° C.∠3+∠4=180° D.∠2+∠4=180° (1) (2) (3) 四、解答题 9、如图,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数. 10、如图,∠1=72°,∠2=72°,∠3=60°,求∠4的度数. 11、如图,AB∥CD,∠A=60°,∠1=2∠2,求∠2的度数. 4查看更多