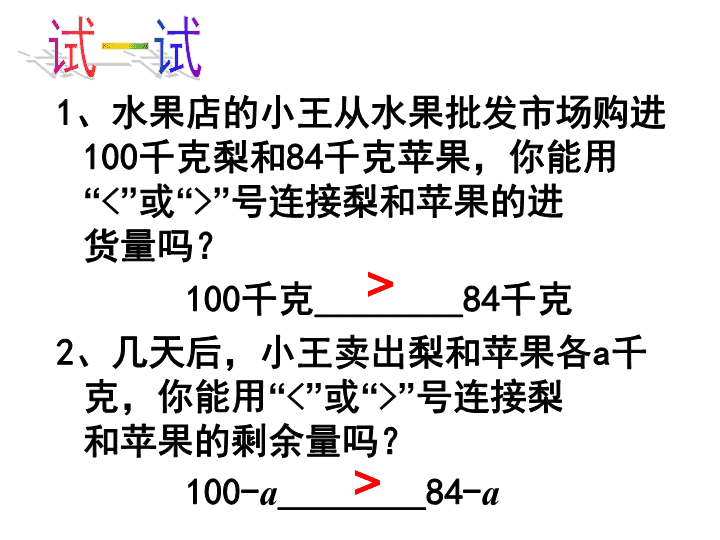
七年级下数学课件《不等式的性质》 (8)_苏科版
苏科版七下11.3不等式性质
1、水果店的小王从水果批发市场购进100千克梨和84千克苹果，你能用“<”或“>”号连接梨和苹果的进货量吗？100千克________84千克2、几天后，小王卖出梨和苹果各a千克，你能用“<”或“>”号连接梨和苹果的剩余量吗？100-a________84-a>>试一试
3.在不等式5>3两边同时加上或减去2， 在横线上填上“<”或“>”号。5+2_____3+2 5-2______3-2>>4.自已写一个不等式，在它的两边同时加上、减去同一个数，看看有什么样的结果？试一试
不等式的两边都加上(或都减去)同一个数或同一个整式，不等号的方向不变.不等式的性质1a>ba+c>b+c(或a-c>b-c)知识点
完成下列填空：2＜32×5____3×52＜32×0.5____3×0.52＜32×（-1）____3×（-1）2＜32×（-5）____3×（-5）2＜32×（-0.5）_____3×(-0.5)你发现了什么？＜＜＞＞＞试一试
不等式的两边都乘以（或除以）同一个正数，不等号的方向不变；不等式的两边都乘以（或除以）同一个负数，不等号的方向改变；不等式的性质2a>b，c>0ac>bca>b，c<0ac
b，c<0，那么acb，c>0，那么ac>bc,不等式的性质2
1.不等式的两边都乘0，结果怎样？2.不等式的性质与等式的性质有什么相同点和不同点？想一想
（1）x-6＜y-6(2)3x＜3y(3)-2x＜-2y（4）x+9＞y+9（5）2x+1＞2y+1（6）-3x-1＞-3y-1不成立不成立成立成立成立不成立例题1已知x＞y，下列不等式一定成立吗？
应用举例例1：将下列不等式化成“x＞a”或“x＜a”的形式：（1）x－5＞－1;（2）－2x＞3;（3）3x＜－9.解：(1)根据不等式的性质1，两边都加上5，得x＞－1+5即x＞4;
应用举例例1：将下列不等式化成“x＞a”或“x＜a”的形式：（1）x－5＞－1;（2）－2x＞3;（3）3x＜－9.解：(2)根据不等式的性质2，两边都除以－2，得x＜－;
应用举例例1：将下列不等式化成“x＞a”或“x＜a”的形式：（1）x－5＞－1;（2）－2x＞3;（3）3x＜－9.解：(3)根据不等式的性质1，两边都除以3，得x＜－3.
例2用“>”或“<”填空：(1)a＋3_____b＋3；(ab)；(3)(a>b)；(4)a－4_____b－4(a－b>0)；(5)若a>0，b>0，则ab_____0；(6)若b<0，则a＋b______a；(7)当a<0时，b_____0时，ab>0．＜＜＜＜＞＞＞
1、如果x＋5＞4，那么两边都可得x＞－12、在－7＜8的两边都加上9可得。3、在5＞－2的两边都减去6可得。4、在－3＞－4的两边都乘以7可得。5、在－8＜0的两边都除以8可得。减去52＜17－1＞－8－21＞－28－1＜0
6、在不等式－8＜0的两边都除以－8可得。7、在不等式－3x＜3的两边都除以－3可得。8、在不等式－3＞－4的两边都乘以－3可得。9、在不等式的两边都乘以－1可得。1＞09＜12
＞＞＞＜如果，那么：①②③④（不等式性质）（不等式性质）（不等式性质）（不等式性质）1221
批改作业：将不等式ax+3≥x–1化成“x≥m”或“x≤n”的形式.下面是小明学完本节后的解答，让我们一起来批改.解：根据不等式的性质1，两边都减去3，得：ax+3-3≥x–1-3即：ax≥x–4根据不等式的性质1，两边都减去x,得：ax-x≥x-x–4即:(a–1)x≥4根据不等式的性质2，两边都除以(a-1),得：x≥
在下列各题横线上填入不等号，使不等式成立．并说明是根据哪一条不等式基本性质．(1)若a-3＜9，则a______12；(2)若-a＜10，则a______-10；(3)若＞-1,则a______-4；(4)若＞0，则a_______0；例题2＜＞＜＞
x＞4x＜－1.5x＜1.5将下列不等式化成“x＞a”或“x＜a”的形式：（1）x-5＞-1（2）-2x＞3（3）2x-1＜2（4）-x＜x＞－例题3
1.（口答）已知a＜b,用“＜”或“＞”号填空：（1）a-3___b-3(2)6a____6b(3)–a___-b(4)a-b____0＜＜＜＞新知运用
2.判断下列各题的推导是否正确？为什么？(1)因为7.5＞5.7，所以-7.5＜-5.7；(2)因为a+8＞4，所以a＞-4；(3)因为4a＞4b，所以a＞b；(4)因为-1＞-2，所以-a-1＞-a-2；(5)因为3＞2，所以3a＞2a．新知运用
3、已知a＜0，用“＜”或“＞”号填空：(1)a+2______2；(2)a-1______-1；(3)3a______0；(4)______0;(5)a2_____0;(6)a3______0(7)a-1______0；(8)|a|______0．＜＜＜＜＜＞＞＞新知运用
将下列不等式化成“x＞a”或“x＜a”的形式：拓展延伸
-a一定小于a吗？为什么？拓展延伸
谈谈这节课你有什么收获?说一说
不等式的两边都加上(或都减去)同一个数或同一个整式，不等号的方向不变.不等式的性质1a>ba+c>b+c(或a-c>b-c)
不等式的两边都乘以（或除以）同一个正数，不等号的方向不变；不等式的两边都乘以（或除以）同一个负数，不等号的方向改变；不等式的性质2a>b，c>0ac>bca>b，c<0ac
查看更多
