七年级下数学课件《互逆命题》课件2_苏科版

七年级下数学课件《互逆命题》课件2_苏科版

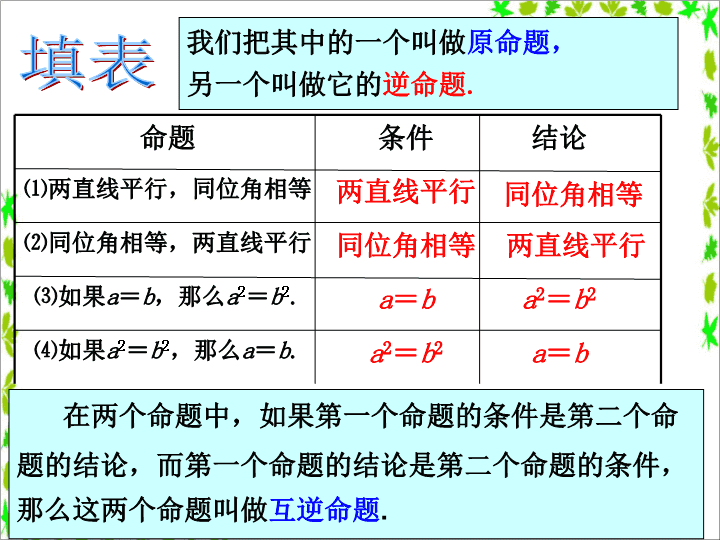
互逆命题 1.命题:2.结构：3.命题真假：回顾 填表a＝ba2＝b2⑷如果a2＝b2，那么a＝b.a2＝b2a＝b⑶如果a＝b，那么a2＝b2.两直线平行同位角相等⑵同位角相等，两直线平行同位角相等两直线平行⑴两直线平行，同位角相等结论条件命题在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题.我们把其中的一个叫做原命题，另一个叫做它的逆命题. 说出下列命题的逆命题，并判定原命题与逆命题的真假.判断(1)同位角相等；相等的角是同位角.(2)面积相等的三角形全等.全等三角形的面积相等.(3)在一个三角形中，等角对等边.在一个三角形中，等边对等角.真命题假命题假命题假命题真命题真命题 思考：每个命题都有逆命题吗？真命题的逆命题是真命题吗？在数学命题中，请举例说出一个原命题是真命题，逆命题是假命题的例子；(4)磁悬浮列车是一种高速行驶时不接触地面的交通工具.高速行驶时不接触地面的交通工具是磁悬浮列车.假命题真 下列说法哪些正确，哪些不正确？（1）每个命题都有逆命题.（2）假命题没有逆命题.（3）真命题的逆命题是真命题.√××辨别 例1证明：平行于同一条直线的两条直线平行.已知：如图12-10，直线a、b、c中，b∥a，c∥a.求证：b∥c.证明：作直线d，使它与直线a、b、c都相交.∵b∥a（已知），∴∠2=∠1（两直线平行，同位角相等）.∵c∥a（已知），∴∠3=∠1（两直线平行，同位角相等）.∴∠2=∠3（等量代换）.∴b∥c（同位角相等，两直线平行）. 例2证明：直角三角形的两个锐角互余.已知：如图12-11，在△ABC中，∠C=90°.求证：∠A+∠B=90°.证明：在△ABC中，∠A+∠B+∠C=180°（三角形三个内角和等于180°）.∴∠A+∠B=180°-∠C（等式性质）.∵∠C=90°.（已知），∴∠A+∠B=180°-90°（等量代换）.即∠A+∠B=90°. ⑴任意作一条线段，并画出它的中垂线⑵线段的中垂线（垂直平分线）有什么性质？AB线段垂直平分线上的点到这条线段两个端点的距离相等ODCP⑶请说出它的逆命题，并证明这个逆命题是真命题.按要求作答： APB已知：如图，ＡＢ是一条线段，Ｐ是一点，且ＰＡ＝ＰＢ.求证：点P在线段AB的垂直平分线上.OC解:这个命题的逆命题是:到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．BPPPPPPA 作PC⊥AB于点O证明:∵PA=PB，PO⊥AB，∴OA=OB（等腰三角形三线合一性质）∴PC是AB的垂直平分线.∴点P在线段AB的垂直平分线上⑵当点P在线段AB上，结论显然成立；⑴当点P不在线段AB上时，显然，上述两个命题可称为互逆命题. 线段垂直平分线性质定理：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上.APB几何语言：∵PA=PB∴点P在AB的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等.线段垂直平分线性质定理的逆命题：结论 例、写出命题“等腰三角形底边上的中点到两腰的距离相等”的逆命题，并证明逆命题是真命题.试试 挑战已知命题：“P是等边三角形ABC内一点.若点P到三边的距离相等，则PA=PB=PC.”证明这个命题，并写出它的逆命题，判断其逆命题成立吗？ 谈谈本节课的收获