七年级上数学课件：5-1 认识一元一次方程 课件（共13张PPT）_北师大版

七年级上数学课件：5-1 认识一元一次方程 课件（共13张PPT）_北师大版

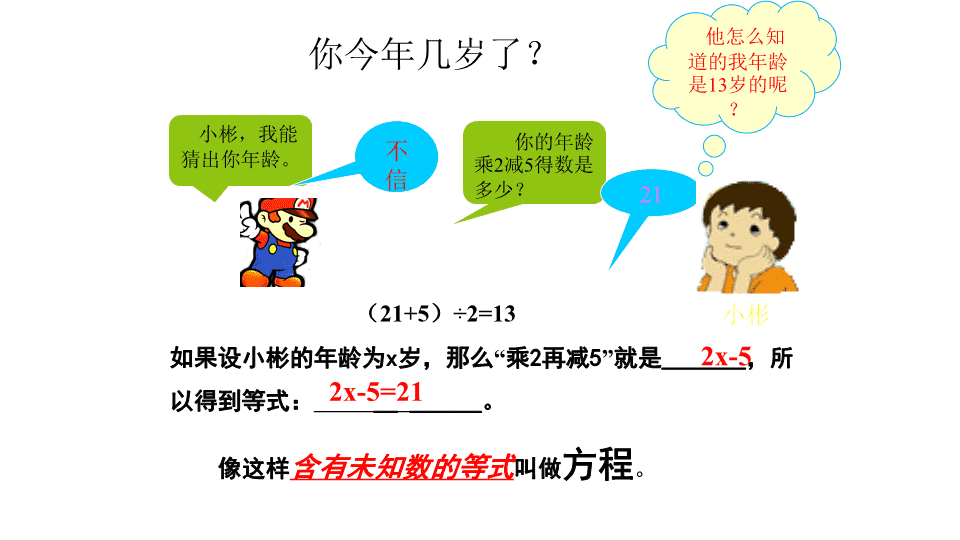
一元一次方程认识一元一次方程 你今年几岁了？小彬，我能猜出你年龄。不信你的年龄乘2减5得数是多少？21小彬他怎么知道的我年龄是13岁的呢？（21+5）÷2=13如果设小彬的年龄为x岁，那么“乘2再减5”就是_______，所以得到等式：________。2x-52x-5=21像这样含有未知数的等式叫做方程。 判断下列各式是不是方程，是的打“√”，不是的打“ｘ”。(1)-2+5=3()(2)3χ-1=0()(3)y=3()(4)χ+y=2()(5)2χ2-5χ+1=0()(6)χy-1=0()(7)2m-n()(8)S=πr2()判断方程①有未知数②是等式ｘ√√√√√ｘ√ 上面的问题中包含哪些已知量、未知量和等量关系?小颖种了一株树苗，开始时树苗高为40厘米，栽种后每周升高约15厘米，大约几周后树苗长高到1米？想一想 思考下列情境中的问题，列出方程。情境140cm100cmx周如果设x周后树苗升高到1米，那么可以得到方程：___。40+15χ=100 情境2某长方形足球场的周长为310米，长和宽之差为25米，这个足球场的长与宽分别是多少米？如果设这个足球场的宽为X米，那么长为(X+25)米。由此可以得到方程：__________。2[χ+(χ+25)]=310(X+25)米X米 情境3第五次全国人口普查统计数据（2001年3月28日新华社公布）截至2000年11月1日0时，全国每10万人中具有大学文化程度的人数为3611人，比1990年7月1日0时增长了153.94%.1990年6月底每10万人中约有多少人具有大学文化程度？如果设1990年6月每10万人中约有x人具有大学文化程度，那么可以得到方程：χ(1+153.94%)=3611 ⑴40+15χ=100⑶χ(1+153.94%)=3611⑵2[χ+(χ+25)]=310三个情境中的方程为：议一议上面情境中的三个方程有什么共同点？在一个方程中，只含有一个未知数χ(元)，并且未知数的指数是1(次)，这样的方程叫做一元一次方程。 练习题1、请联系生活中的例子编一道应用题，并列出方程。2、甲、乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1分，负一场得0分。甲队与乙队一共比赛了10场，甲队保持了不败记录，一共得了22分，甲队胜了多少场？平了多少场？解：设甲队胜了x场，则乙胜了（10－x）场由题意得3x+(10－x)=22 等式的基本性质：等式的性质1：等式两边加（或减）同一个代数式，所的结果仍是等式。等式的性质2：等式两边乘（或除）（除数不能为0）同一个数，所的结果仍是等式。注意与小学所学等式性质的区别 例1 利用等式的性质解下列方程：(1)x＋2=5;（2）3=x-5方法一：用加减法互为逆运算方法一：用等式的基本性质请同学们写出详细步骤(1)x+2-2=5-2x=3(2)x-5+5=3+5x=8 下列用等式性质进行的变形中，那些是正确的，并说明理由（1）若x=y，则5+x=5+y（2）若x=y，则5-x=5-y（3）若x=y，则5x=5y（4）若x=y，则（5）若，则bx=by（6）若2x（x-1）=x，则2（x-1）=1正确的是（1）（2）（3）（4） 1.通过对“你今年几岁了”的探讨，我们知道数学就在我们身边，并在对其它实际问题研究中感受了方程作为刻画现实世界有效模型的作用。2.通过观察归纳出方程及一元一次方程的概念．3.在分析课本设置的例题的过程中初步体会了列方程的“核心”与“关键”。小结