七年级下数学课件《多边形的内角和与外角和》 (16)_苏科版

七年级下数学课件《多边形的内角和与外角和》 (16)_苏科版

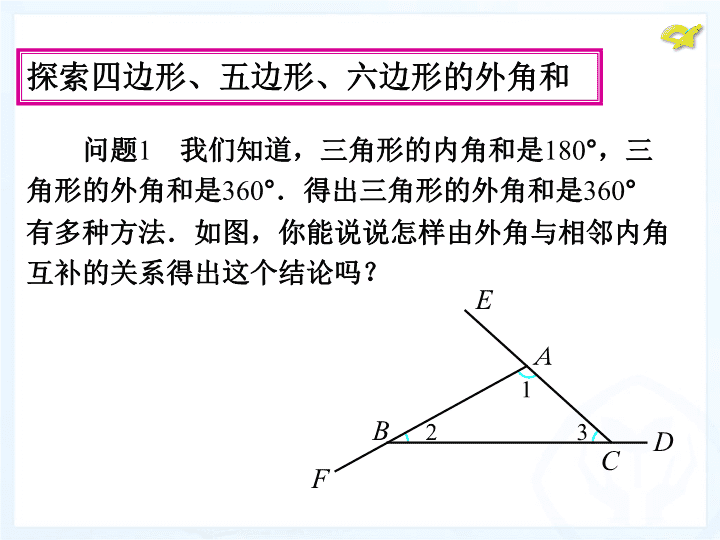
7.5多边形的内角和与外角和（3）---多边形的外角和 学习目标：探索并掌握多边形的外角和公式．学习重点：探索并掌握多边形的外角和公式． 问题1我们知道，三角形的内角和是180°，三角形的外角和是360°．得出三角形的外角和是360°有多种方法．如图，你能说说怎样由外角与相邻内角互补的关系得出这个结论吗？探索四边形、五边形、六边形的外角和ＡBCDEF123 探索四边形、五边形、六边形的外角和由∠1+∠BAE=180°，∠2+∠CBF=180°，∠3+∠ACD=180°，得∠1+∠2+∠3+∠BAE+∠CBF+∠ACD=540°．由∠1+∠2+∠3=180°，得∠BAE+∠CBF+∠ACD=540°-180°=360°．ＡBCDEF123 问题2如图，你能仿照上面的方法求四边形的外角和吗？探索四边形、五边形、六边形的外角和ＡBC123D4由∠BAD+∠1=180°，∠ABC+∠2=180°，∠BCD+∠3=180°，∠ADC+∠4=180°，得∠BAD+∠1+∠ABC+∠2+∠BCD+∠3+∠ADC+∠4=180°×4．由∠BAD+∠ABC+∠BCD+∠ADC=180°×2，得∠1+∠2+∠3+∠4=180°×4-180°×2=360°． 探索四边形、五边形、六边形的外角和问题3五边形的外角和等于多少度？六边形呢？仿照上面的方法试一试．类比求三角形、四边形的外角和的方法求出五边形的外角和是360°，六边形的外角和是360°（解答过程略）． 探索n边形的外角和问题4你能仿照上面的方法求n边形（n是不小于3的任意整数）的外角和吗？因为n边形的每个内角与它相邻的外角是邻补角，它们的和是180°，所以n边形内角和加外角和等于n·180°，所以，n边形的外角和为：n·180°-（n-2）·180°=360°．任意多边形的外角和等于360°． 探索n边形的外角和我们也可以在问题4的基础上这样理解多边形外角和等于360°．如图，从多边形的一个顶点A出发，沿多边形的各边走过各顶点，再回到点A，然后转向出发的方向．A 探索n边形的外角和我们也可以在问题4的基础上这样理解多边形外角和等于360°．在行程中转过的各个角的和，就是多边形的外角和．由于走了一周，所转过的各个角的和等于一个周角，所以多边形外角和等于360°．A 巩固多边形外角和公式解：设这个多边形为n边形，根据题意，可列方程（n-2）×180°=3×360°．解得n=8．答：它是八边形．例1一个多边形的内角和等于它的外角和的3倍，它是几边形？ 四边形课堂练习练习1一个多边形的内角和与外角和相等，它是几边形？ 解：不存在．理由：如果存在这样的多边形，设它的一个外角为x，则对应的内角为180°-x，于是x=180°-x，解得x=150°.练习2是否存在一个多边形，它的每个内角都等于相邻外角的？为什么？这个多边形的边数为：360°÷150°=2.4，而边数应是整数，因此不存在这样的多边形．课堂练习 课堂小结（1）本节课学习了哪些主要内容？（2）我们是怎样得到“多边形外角和等于360°”这一结论的？