- 2021-07-01 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
天津市天津一中11-12学年高二数学上学期期中考试试题 文
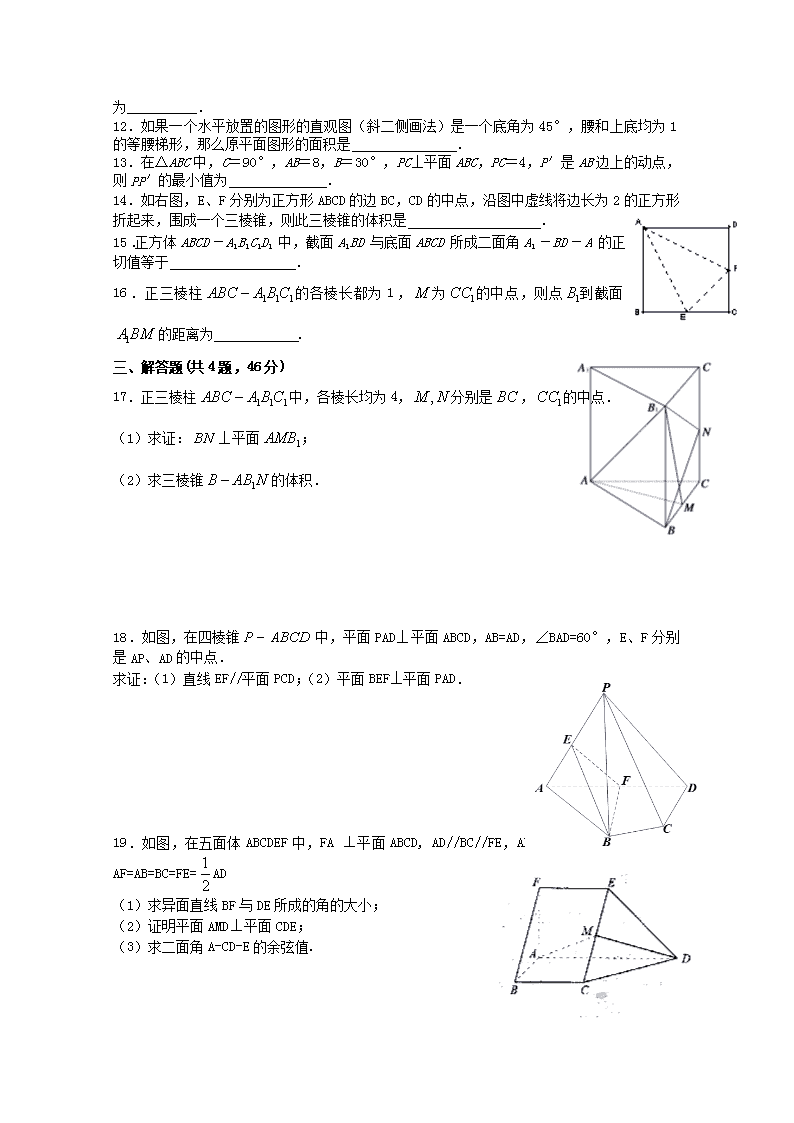
天津一中2011—2012学年第一学期期中 高二数学试卷(文科) 一、选择题(每题3分,共30分) 1.如图是一个几何体的三视图,侧视图与正视图均为矩形,俯视图为 正三角形,尺寸如图,则该几何体的侧面积为( ) A.6 B.12 C.24 D.3 2.已知正方体的外接球的体积为π,则该正方体的表面积为( ) A. B. C. D.32 3.一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面( ) A.至多只能有一个是直角三角形 B.至多只能有两个是直角三角形 C.可能都是直角三角形 D.必然都是非直角三角形 4.对于平面和直线,内至少有一条直线与直线 ( ) A.平行 B. 垂直 C.异面 D.相交 5.已知是两条不同直线,是三个不同平面,正确命题的个数是( ) ①若,,则// ②若,,则// ③若,,则 ④若//,//,则// A B C S E F ⑤若//,//,则// A.1 B.2 C.3 D.4 6.如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点, 那么异面直线EF与SA所成的角等于( ) A. 90° B.45° C.60° D.30° 7.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( ) A.BD∥平面CB1D1 B.AC1⊥BD C.AC1⊥平面CB1D1 D.异面直线AD与CB1所成的角为60° 8.如图,在长方体中,,, 则与平面所成角的正弦值为( ) A. B. C. D. 9.已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( ) A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形 10.如图所示,在斜三棱柱ABC-A1B1C1的底面△ABC中,∠A=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( ) A.直线AC上 B.直线AB上 C.直线BC上 D.△ABC内部 二、填空题(每题4分,共24分) 11.中, ,将三角形绕AC边旋转一周所成的几何体的体积为__________. 12.如果一个水平放置的图形的直观图(斜二侧画法)是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是 . 13.在△ABC中,C=90°,AB=8,B=30°,PC⊥平面ABC,PC=4,P′是AB边上的动点,则PP′的最小值为 . 14.如右图,E、F分别为正方形ABCD的边BC,CD的中点,沿图中虚线将边长为2的正方形折起来,围成一个三棱锥,则此三棱锥的体积是 . 15.正方体ABCD-A1B1C1D1中,截面A1BD与底面ABCD所成二面角A1-BD-A的正切值等于 . 16.正三棱柱的各棱长都为1,为的中点,则点到截面的距离为 . 三、解答题(共4题,46分) 17.正三棱柱中,各棱长均为4,分别是,的中点. (1)求证:⊥平面; (2)求三棱锥的体积. 18.如图,在四棱锥中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点. 求证:(1)直线EF//平面PCD;(2)平面BEF⊥平面PAD. 19.如图,在五面体ABCDEF中,FA 平面ABCD, AD//BC//FE,ABAD,M为EC的中点,AF=AB=BC=FE=AD (1)求异面直线BF与DE所成的角的大小; (2)证明平面AMD平面CDE; (3)求二面角A-CD-E的余弦值. 20.如图,在四棱锥中, 底面是的中点. A P E B C D (1)证明; (2)证明平面; (3)求二面角的正切值. 参考答案: 一、选择题: 1.C 2.D 3.C 4.B 5.A 6.B 7.D 8.A 9.C 10.B 二、填空题: 11. 12. 13. 14. 15. 16. 三、解答题: 17. (1)证明:正三棱柱ABC-A1B1C1中 BB1⊥平面ABC ∴BB1⊥AM ……………………4分 在正△ABC中,M是BC中点 ∴AM⊥BC 又BCBB1=B ∴AM⊥平面BC1 ∴AM⊥BN ……………………2分 在正方形BC1中 Rt△BCN≌Rt△B1BM ∴∠2=∠1 ∵∠3+∠2=90o ∴∠1+∠3=90o ∴BN⊥B1M ……………………2分 又AMB1M=M ∴BN⊥平面AB1M ……………………1分 (2) ……………………3分 ……………………2分 18.证明: (1)因为E、F分别是AP、AD的中点, 又 直线EF‖平面PCD (2) F是AD的中点, 又平面PAD⊥平面ABCD, 所以,平面BEF⊥平面PAD。 19. (1)BCFE ……………………1分 ∴BCEF是□ ∴BF//CE ∴∠CED或其补角为BF与DE所成角 ……………………2分 取AD中点P连结EP和CP ∵FEAP ∴FAEP 同理ABPC 又FA⊥平面ABCD ∴EF⊥平面ABCD ∴EP⊥PC、EP⊥AD 由AB⊥AD PC⊥AD 设FA=a,则EP=PC=PD=a CD=DE=EC=a ∴△ECD是正三角形 ∴∠CED=60o ∴BF与DE成角60o ……………………2分 (2)∵DC=DE,M为EC中点 ∴DM⊥EC 连结MP,则MP⊥CE 又DMMP=M ∴DE⊥平面ADM ……………………3分 又CE平面CDE ∴平面AMD⊥平面CDE ……………………1分 (3)取CD中点Q,连结PQ和EQ ∵PC=DQ ∴PQ⊥CD,同理EQ⊥CD ∴∠PQE为二面角的平面角 ……………………2分 在Rt△EPQ中, ∴二面角A-CD-E的余弦值为 20. (1)证明: ∵PA⊥底面ABCD,CD平面ABCD ∴PA⊥CD 又AC⊥CD,ACPA=A ∴CD⊥平面PAC,又AE平面PAC ∴CD⊥AE (2)证明: ∵PA⊥底面ABCD,AB平面ABCD ∴PA⊥AB 又AD⊥AB,ADPA=A ∴AB⊥平面PAD,又PD平面PAD ∴AB⊥PD 由PA=AB=BC,∠ABC=60o 则△ABC是正三角形 ∴AC=AB ∴PA=PC ∵E是PC中点 ∴AE⊥PC 由(1)知AE⊥CD,又CDPC=C ∴AE⊥平面PCD ∴AE⊥PD 又AB⊥PD,ABAE=A ∴PD⊥平面ABE (3)过E点作EM⊥PD于M点连结AM 由(2)知AE⊥平面PCD ∴AM⊥PD ∠AME是二面角A-PD-C的正切值 设AC=a 在Rt△AEM中 查看更多