内蒙古包头市回民中学2019-2020学年高二上学期期中考试数学（理）试卷

内蒙古包头市回民中学2019-2020学年高二上学期期中考试数学（理）试卷

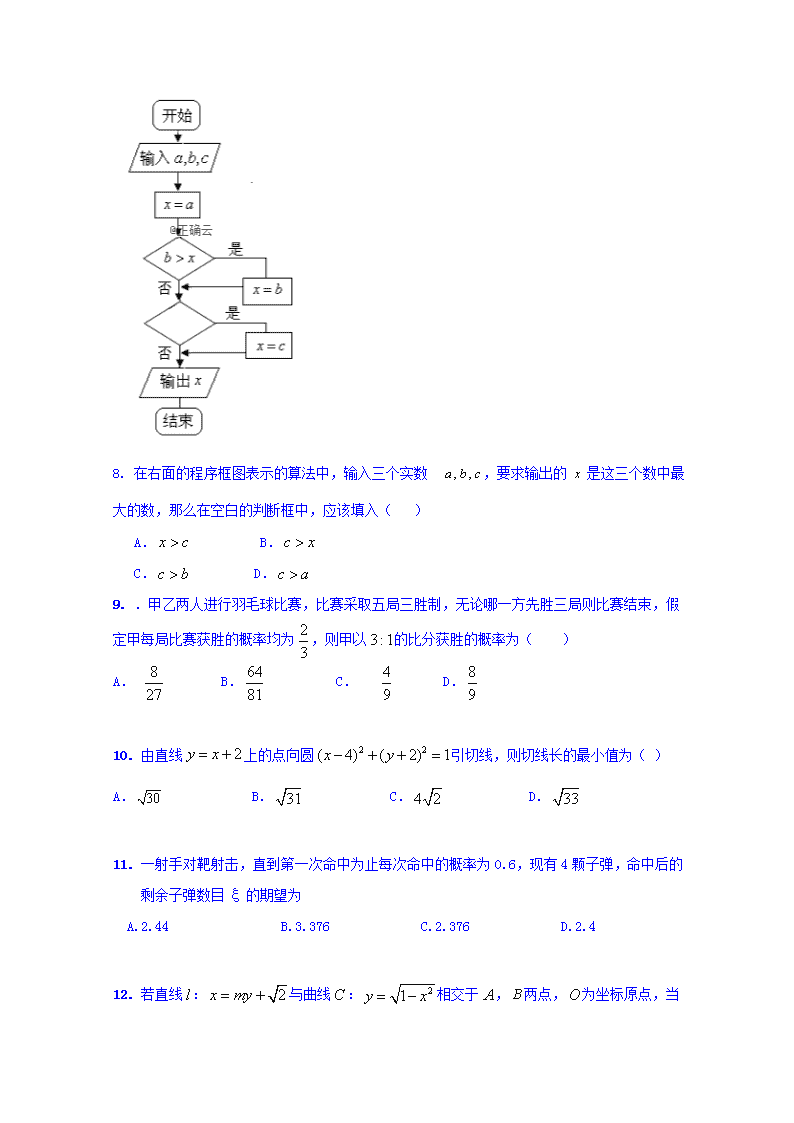
理科数学 一、选择题（本题共12小题，每小题5分，共60分）‎ ‎1. 在下列各图中，每个图的两个变量具有相关关系的图是（ ）‎ ‎ ‎ ‎ （1） （2） （3） （4）‎ A．（1）（2） B．（1）（3） 　 C．（2）（4） D．（2）（3）‎ ‎2. 4名同学分别从6、8、9中选一个数字作为自己的幸运数，共有多少种不同的选法 （ ）‎ A．4 B．24 C．81 D．64 ‎ ‎3. 圆在点处的切线方程为（ ）‎ A． B． C． D．‎ ‎4.用随机数表法从100名学生（男生25人）中抽选20人进行评教，某男生被抽到的机率是（ ）‎ A、 B、 C、 D、‎ ‎5. 投掷红、蓝两个骰子，事件A=“红骰子出现4点”，事件B=“蓝骰子出现的点数是偶数”，‎ 则P（A|B）=（ ）‎ A. B. C. D. ‎ ‎6. 某台小型晚会由6个节目组成，演出顺序有如下要求：节目甲必须排在前两位，节目乙不能排在第一位，节目丙必须排在最后一位．该台晚会节目演出顺序的编排方案共有(　　)‎ A．36种 B．42种 C．48种 D．54种 ‎7. 二项式的展开式中只有第六项的二项式系数最大，则展开式中的常数项是( )‎ A. 180 B. 90 C. 45 D. 360‎ ‎8. 在右面的程序框图表示的算法中，输入三个实数 ，要求输出的是这三个数中最大的数，那么在空白的判断框中，应该填入（ ）‎ A． B．‎ C． D． ‎ ‎9. ．甲乙两人进行羽毛球比赛，比赛采取五局三胜制，无论哪一方先胜三局则比赛结束，假定甲每局比赛获胜的概率均为，则甲以的比分获胜的概率为（ ）‎ A． B． C． D． ‎ ‎10. 由直线上的点向圆引切线，则切线长的最小值为（ ）‎ A． B． C． D．‎ ‎11. 一射手对靶射击，直到第一次命中为止每次命中的概率为0.6，现有4颗子弹，命中后的剩余子弹数目ξ的期望为 A.2.44 B.3.376 C.2.376 D.2.4‎ ‎12. 若直线：与曲线：相交于，两点，为坐标原点，当 的面积取最大值时，实数的值为(　　)‎ A． B． C． D．‎ 二、填空题（每小题5分，共20分）‎ ‎13. 已知圆与直线交于，两点，过，分别作轴的垂线，且与轴分别交于，两点，若，则_________.‎ ‎14.某人午觉醒来，发现表停了，他打开收音机想听电台报时，则他等待的时间不多于6分钟的概率是_________.‎ ‎15. (x＋)(2x－)5的展开式中各项系数的和为2，则该展开式中常数项为_________.‎ ‎16. 直线与圆相交于M，N两点，若．‎ ‎ 则的取值范围是__________.‎ 三、解答题（共70分）‎ ‎17. （10分）已知(a2＋1)n展开式中各项系数之和等于5的展开式的常数项，‎ 而(a2＋1)n展开式的二项式系数最大的项等于54，求a的值 ‎18.（12分）已知圆 x2+y2=9内有一点P（1，2），AB为过P点且倾斜角为的弦。‎ ‎（1）当α=135。时，求AB的长；‎ ‎（2）当弦AB被点P平分时，求直线AB的方程。‎ ‎ (3)求过点P的弦的中点的轨迹方程。‎ ‎19.（12分）如图，正三棱柱ABC－A1B1C1的所有棱长都为2，D为CC1中点．‎ ‎（1）求证：AB1⊥平面A1BD；‎ ‎ （2）求锐二面角A－A1D－B的余弦值；‎ ‎20.某工厂有两个车间生产同一种产品，第一车间有工人200人，第二车间有工人400人，为比较两个车间工人的生产效率，采用分层抽样的方法抽取工人，并对他们中每位工人生产完成一件产品的时间（单位：分别进行统计，得到下列统计图表（按照，，，，，，，分组）． ‎ 分组 频数 ‎，‎ ‎2‎ ‎，‎ ‎4‎ ‎，‎ ‎10‎ ‎，‎ ‎4‎ 合计 ‎20‎ ‎ ‎ ‎ 第一车间样本频数分布表 ‎（Ⅰ）分别估计两个车间工人中，生产一件产品时间小于的人数；‎ ‎（Ⅱ）分别估计两车间工人生产时间的平均值，并推测哪个车间工人的生产效率更高？（同一组中的数据以这组数据所在区间中点的值作代表）‎ ‎（Ⅲ）从第一车间被统计的生产时间小于的工人中，随机抽取3人，记抽取的生产时间小于的工人人数为随机变量，求的分布列及数学期望．‎ ‎21.在平面直角坐标系xoy中，经过点（0，3）且斜率为k在直线l与圆x2+y2=4有两个不同的交点P 、Q. ‎ ‎（1）求k的取值范围；‎ ‎（2）设A(2,0),B(0,1)，若向量与共线，求k的值。‎ ‎22..某面包店推出一款新面包，每个面包的成本价为4元，售价为10元，该款面包当天只出一炉（一炉至少15个，至多30个），当天如果没有售完，剩余的面包以每个2元的价格处理掉．为了确定这一炉面包的个数，该店记录了这款新面包最近30天的日需求量（单位：个），整理得下表 日需求量 ‎15‎ ‎18‎ ‎21‎ ‎24‎ ‎27‎ 频数 ‎10‎ ‎8‎ ‎7‎ ‎3‎ ‎2‎ ‎（1）根据表中数据可知，频数与日需求量（单位：个）线性相关，求关于的线性回归方程；‎ ‎（2）以30天记录的各日需求量的频率代替各日需求量的概率．若该店这款新面包出炉的个数为24，记当日这款新面包获得的总利润为（单位：元）‎ ‎（ⅰ）若日需求量为15个，求；‎ ‎（ⅱ）求的分布列及其数学期望 相关公式：，‎ ‎，‎ 二．填空；13.1或-7 ，14. 15.40 ,16. ‎ 三、解答题 ‎19. 【解析】（1）取BC中点O，连结AO．∵△ABC为正三角形，∴AO⊥BC．‎ ‎∵在正三棱柱ABC－A1B1C1中，平面ABC⊥平面BCC1B1，∴AO⊥平面BCC1B1． ‎ 取B1C1中点O1，以O为原点，，，的方向为x，y，z轴的正方向建立空间直角坐标系：‎ ‎，如图所示，则B(1，0，0)，D(1，1，0)，‎ A1(0，2，)，A(0，0，)，B1(1，2，0)，‎ ‎∴，，．‎ ‎∴，，‎ ‎∴，，∴AB1平面A1BD．‎ ‎（2）设平面A1AD的法向量为．‎ ‎，．‎ ‎∵，，∴，∴，，‎ 令得为平面A1AD的一个法向量．‎ 由（1）知AB1平面A1BD，为平面A1BD的法向量，‎ ‎∴．‎ ‎∴锐二面角A－A1D－B的大小的余弦值为．‎ ‎20. 【解析】：估计第一车间生产时间小于的工人人数为（人，（2分）‎ 估计第二车间生产时间小于的工人人数为：‎ ‎（人．‎ 第一车间生产时间平均值约为：‎ ‎．‎ 第二车间生产时间平均值约为：‎ ‎，‎ ‎，第二车间工人生产效率更高．‎ 由题意得，第一车间被统计的生产时间小于的工人有6人，‎ 其中生产时间小于的有2人，从中抽取3人，随机变量服从超几何分布，‎ 可取值为0，1，2，‎ ‎，‎ ‎，‎ ‎，‎ 的分布列为：‎ ‎0‎ ‎1‎ ‎2‎ 数学期望 ‎21.‎ ‎22. 【解析】（1）根据近30天的数据，，，‎ ‎， ‎ ‎．‎ 所以回归方程为 ‎(2)（Ⅰ）若日需求量为15个，则元，‎ ‎ （Ⅱ）若日需求量为18个，则元，‎ 若日需求量为21个，则元，‎ 若日需求量为24个或者27个，则．‎ 所以的分布列为：‎ ‎72‎ ‎96‎ ‎120‎ ‎144‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 所以元．‎