2018-2019学年安徽省阜阳市第三中学高一竞培中心下学期第二次调研考试数学试题

2018-2019学年安徽省阜阳市第三中学高一竞培中心下学期第二次调研考试数学试题

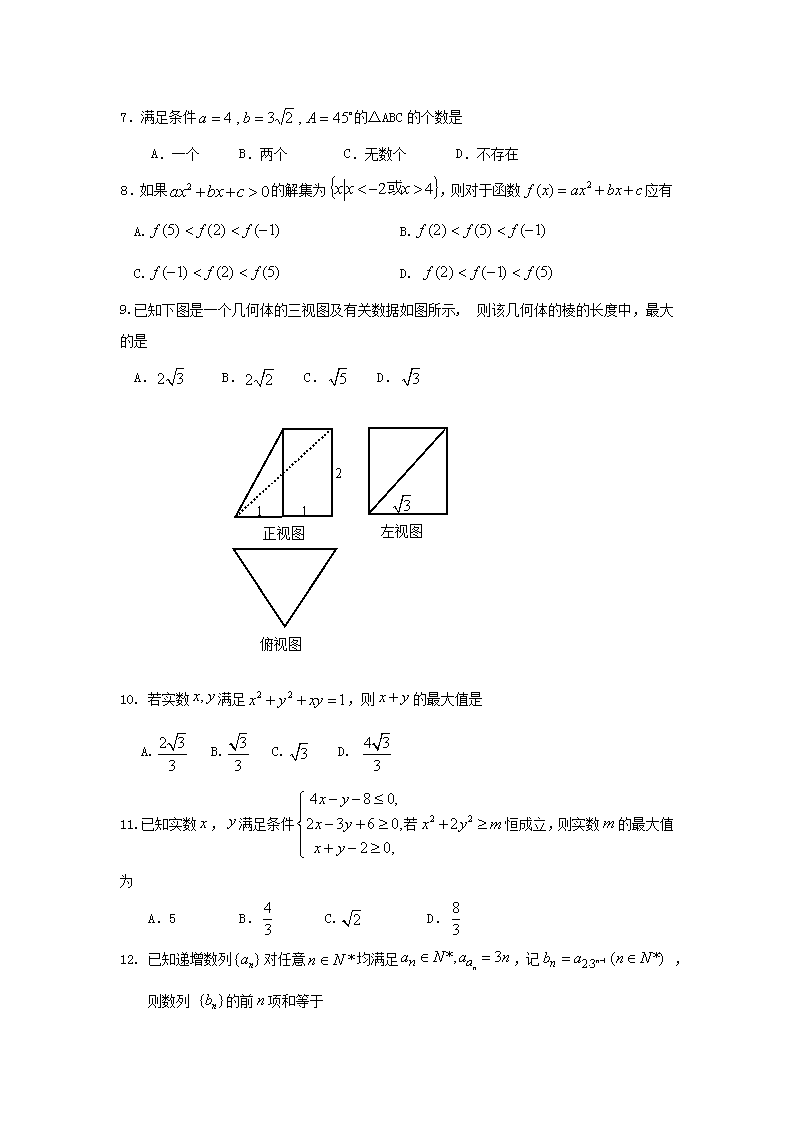
‎ ‎ ‎2018-2019学年安徽省阜阳市第三中学高一竞培中心下学期第二次调研考试数学试题 ‎ 一、选择题：本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.‎ ‎1. 直线的倾斜角为 ‎ A. B. C. D. ‎ ‎2. 设函数在上可导，则等于（ ）‎ ‎ A． B． C． D．以上都不对 ‎3. 若直线和直线相互垂直,则a值为 ‎ ‎ A．0 B．1 C．0或1 D．0或－1 ‎ ‎4. 若数列满足－＝d(n∈N*，d为常数)，则称数列为“调和数列”．已知正项数列{}为“调和数列”，且b1＋b2＋…＋b9＝90，则b4·b6的最大值是 ‎ A．10 B．100 C．200 D．400‎ ‎5．下列四个结论：‎ ‎⑴两条直线和同一个平面平行，则这两条直线平行.‎ ‎⑵两条直线没有公共点，则这两条直线平行.‎ ‎⑶两条直线都和第三条直线垂直，则这两条直线平行.‎ ‎⑷一条直线和一个平面内无数条直线没有公共点，则这条直线和这个平面平行.其中正确的个数为 A.0 B.1 C.2 D. 3‎ ‎6. 圆和圆交于A、B两点，则AB的垂直平分线的方程是 A. x+y+3=0 B. 2x-y-5=0 C. 3x-y-9=0 D. 4x-3y+7=0‎ ‎7．满足条件的△ABC的个数是 A．一个 B．两个 C．无数个 D．不存在 ‎8．如果的解集为，则对于函数应有 ‎ A. B.‎ C. D. ‎ ‎9.已知下图是一个几何体的三视图及有关数据如图所示, 则该几何体的棱的长度中，最大的是 A． B． C． D．‎ 正视图 左视图 俯视图 ‎1‎ ‎1‎ ‎2‎ ‎10. 若实数满足，则的最大值是 ‎ A. B. C. D. ‎ ‎11. 已知实数，满足条件若恒成立，则实数的最大值为 ‎ A．5 B． C. D．‎ ‎12. 已知递增数列对任意均满足，记 ，则数列 的前项和等于 A. B. C. D. ‎ 二、本大题共4小题,每小题5分,共20分,请将答案填在答题卷的指定位置.‎ ‎13. 直线必过一定点，则定点的坐标为 .‎ ‎14. 设函数在内可导，且则＝________.‎ ‎15. 已知三棱锥A-BCD中，BC⊥CD，AB=AD=，BC=1，CD=，则该三棱锥外接球的体积为 ‎ _______.‎ ‎16. 在中，，，是的一个三等分点，则的最大值是 ．‎ 三、本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.‎ ‎17.（本小题满分10分）‎ ‎ 如图：在三棱锥中，已知点、、分别为棱、、的中点.‎ ‎（1）求证：∥平面；‎ ‎（2）若，，求证：平面⊥平面.‎ ‎ ‎ ‎ ‎ ‎18．（本小题满分12分）‎ 已知数列的前项和为，且满足（N）．‎ （1） 求数列的通项公式；（2）求数列的前项和．‎ ‎19.（本小题满分12分）‎ ‎ 某营养师要为某个儿童预定午餐和晚餐．已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素；一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素．另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素．如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐?‎ ‎20．（本小题满分12分）‎ ‎ 在中，内角所对的边分别为,已知，且成等比数列.‎ ‎（1）求；‎ ‎（2）若，求的值.‎ ‎21. （本小题满分12分）‎ ‎ 设各项均为正数的数列的前项和为，且满足．‎ ‎（1）求的值；‎ ‎（2）求数列的通项公式；‎ ‎（3）证明：对一切正整数，有 ‎22. （本小题满分12分）‎ ‎ 已知点及圆：.‎ ‎（1）若直线过点且与圆心的距离为1，求直线的方程；‎ ‎（2）设过P直线与圆交于、两点，当时，求以为直径的圆的方程；‎ ‎（3）设直线与圆交于，两点，是否存在实数，使得过点的直线垂直平分弦？若存在，求出实数的值；若不存在，请说明理由．‎ ‎ 阜阳三中2018—2019学年竞培中心竞一年级二调 数学答案 ‎1. B2. A 3. C4. B5．A6. C7． D8． D9. B 10. A11. D12. D ‎ ‎ 13. （-4，-2） 14. 3 15. 16. ‎ ‎17. 证明：（Ⅰ）∵是的中位线，∴∥.又∵平面，平面，‎ ‎∴∥平面. ‎ ‎（Ⅱ）∵,，∴.∵,，∴.‎ 又∵平面，平面，，∴平面，又∵平面，‎ ‎∴平面⊥平面. ‎ ‎18． 解：(Ⅰ)当时,,解得； 当时,,,两式相减得, 化简得,所以数列是首项为,公比为的等比数列.所以.‎ ‎ (Ⅱ)由(Ⅰ)可得,所以,‎ ‎ 两式相减得 , ‎ ‎ 所以数列的前项和. ‎ ‎19. 为该儿童分别预订个单位的午餐和晚餐，共花费元，则 ‎，且满足以下条件 ‎，即，做出可行域（图略）作直线，‎ 平移直线至，当 经过C点时，可使达到最小值．‎ 由 即，‎ 此时，‎ 答: 午餐和晚餐分别预定4个单位和3个单位，花费最少z=22元．‎ ‎20．（I），.由正弦定理得，又A∈（0，π），..（II）由（I）知，，由余弦定理得，，，，又成等比数列，所以，由正弦定理得.∵， ， . ‎ ‎21. （Ⅰ）所以，‎ ‎（Ⅱ）‎ ‎（Ⅲ）‎ ‎22. 解：（Ⅰ）设直线的斜率为（存在）则方程为. 又圆C的圆心为，半径，‎ 由 ， 解得.所以直线方程为， 即 . ‎ 当的斜率不存在时，的方程为，经验证也满足条件. ‎ ‎（Ⅱ）由于，而弦心距，所以.所以为的中点.‎ 故以为直径的圆的方程为. ‎ ‎（Ⅲ）把直线即．代入圆的方程，‎ 消去，整理得．‎ 由于直线交圆于两点，‎ 故，即，解得．‎ 则实数的取值范围是．设符合条件的实数存在，‎ 由于垂直平分弦，故圆心必在上．‎ 所以的斜率，而，所以．‎ 由于，故不存在实数，使得过点的直线垂直平分弦． ‎