数学文卷·2019届湖南省醴陵二中、醴陵四中高二上学期期末联考（2018-01）

数学文卷·2019届湖南省醴陵二中、醴陵四中高二上学期期末联考（2018-01）

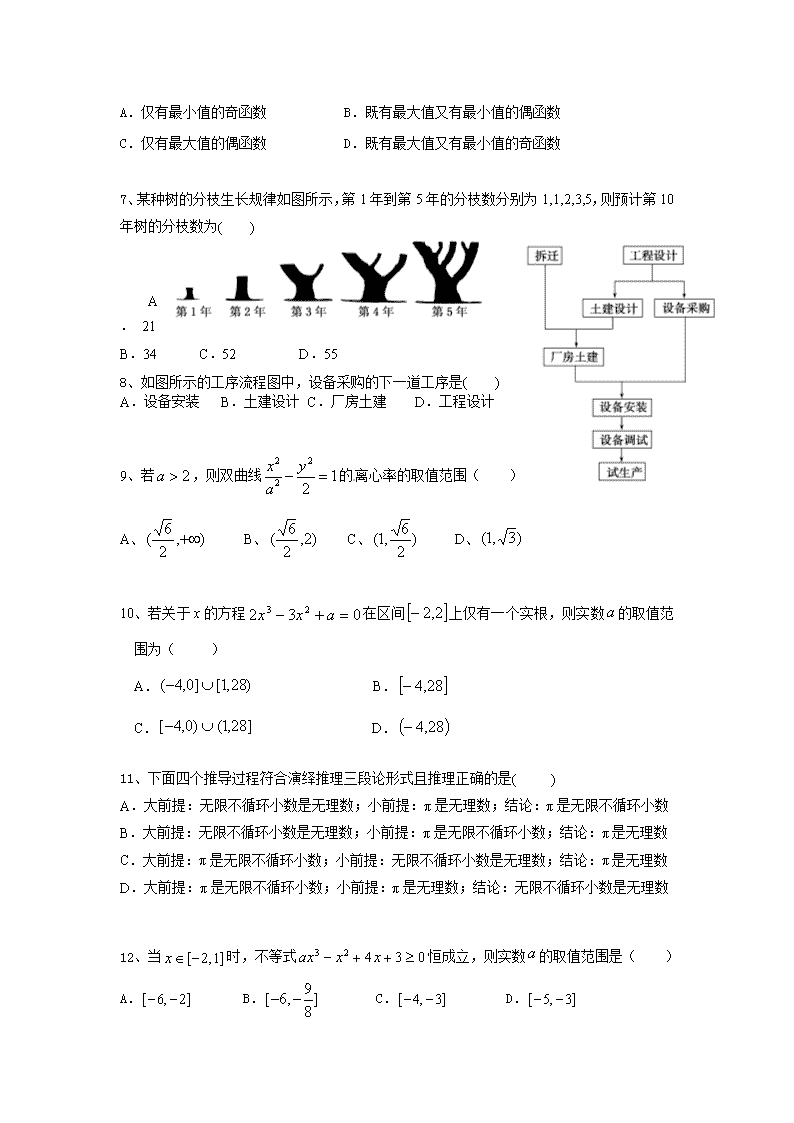
醴陵二中，醴陵四中 ‎2017年下学期两校联考高二年级数学（文）科期末考试试卷 命题学校：醴陵二中 命题人：贺建军 审题人：宁盼 ‎（时间120分钟，满分150分）‎ 一、选择题：（每小题5分，共计60分）‎ ‎1、若将复数表示为，是虚数单位)的形式,则的值为( )‎ ‎ A．-2 B． C．2 D． ‎ ‎2、给出如下四个命题：‎ ‎①若“或”为假命题，则，均为假命题；‎ ‎②命题“若且，则”的否命题为“若，则”； ‎ ‎③在中，“”是“”的充要条件；‎ ‎④命题“若”的逆否命题为真命题。其中正确命题的个数是（ ）‎ ‎ A．3 B．2 C．1 D．0‎ ‎3、已知变量之间具有线性相关关系，其散点图如图所示，则其回归方程可能为（ ）‎ A. B. ‎ C. D. ‎ ‎4、已知双曲线的离心率为，则的渐近线方程为（ ）‎ A． B． C． D．‎ ‎5、下面四个条件中,使成立的充分不必要的条件是（ ）‎ A. B. C. D. ‎ ‎6、已知，则函数是( )‎ A．仅有最小值的奇函数 B．既有最大值又有最小值的偶函数 C．仅有最大值的偶函数 D．既有最大值又有最小值的奇函数 ‎7、某种树的分枝生长规律如图所示，第1年到第5年的分枝数分别为1,1,2,3,5，则预计第10年树的分枝数为( )‎ A．21 B．34 C．52 D．55‎ ‎8、如图所示的工序流程图中，设备采购的下一道工序是( )‎ A．设备安装 B．土建设计 C．厂房土建 D．工程设计 ‎9、若，则双曲线的离心率的取值范围（ ）‎ A、 B、 C、 D、‎ ‎10、若关于x的方程在区间上仅有一个实根，则实数的取值范围为（ ）‎ A． B． ‎ C． D．‎ ‎11、下面四个推导过程符合演绎推理三段论形式且推理正确的是( )‎ A．大前提：无限不循环小数是无理数；小前提：π是无理数；结论：π是无限不循环小数 B．大前提：无限不循环小数是无理数；小前提：π是无限不循环小数；结论：π是无理数 C．大前提：π是无限不循环小数；小前提：无限不循环小数是无理数；结论：π是无理数 D．大前提：π是无限不循环小数；小前提：π是无理数；结论：无限不循环小数是无理数 ‎12、当时，不等式恒成立，则实数的取值范围是（ ）‎ A． B． C． D． ‎ 二、填空题（每小题5分，共20分）‎ ‎13、已知命题“，使”是假命题，则实数的取值范围是 ‎ ‎ ‎14、函数的图象在点处的切线方程为,为的导函数，则___ ____‎ ‎15、已知椭圆的中心在坐标原点，离心率为，的右焦点与抛物线的焦点重合，是的准线与椭圆的两个交点，则 .‎ ‎16、已知f (x)＝x3－6x2＋9x－abc，a＜b＜c，且f (a)＝f (b)＝f (c)＝0.现给出如下结论：①f(0)f(1)＞0; ②f(0)f(1)＜0； ③f(0)f(3)＞0; ④f(0)f(3)＜0.‎ 其中正确结论的序号是_____ ___．‎ 三、解答题：（共70分）‎ ‎17、（本小题满分10分）设是实数,已知命题函数的最小值小于；已知命题： “方程表示焦点在轴上的椭圆”，若为真命题，为假命题，求实数的取值范围。‎ ‎18、（本小题满分12分）已知抛物线，过点引一条弦使它恰好被点平分，求这条弦所在的直线方程及.‎ ‎19、( 本小题满分12分)某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主). ‎ ‎(1)根据茎叶图,帮助这位同学说明这30位亲属的饮食习惯.‎ ‎(2)根据以上数据完成如下2×2列联表.‎ 主食蔬菜 主食肉类 总计 ‎50岁以下 ‎50岁以上 总计 ‎(3)能否有99％的把握认为其亲属的饮食习惯与年龄有关?‎ ‎ ‎ ‎20、(本小题满分分)已知函数，当和时，取得极值．‎ ‎(1)求的值； ‎ ‎(2)若函数的极大值大于20，极小值小于5，试求的取值范围．‎ ‎21、（本小题满分12分）椭圆的离心率为，长轴端点与短轴端点间的距离为.‎ ‎（1）求椭圆的方程；‎ ‎（2）过点的直线与椭圆交于两点，为坐标原点，当为直角时，求直线的斜率.‎ ‎22、（本题满分12分）已知函数．‎ ‎(1)求函数的单调区间；‎ ‎(2)若函数的图象在点处的切线的倾斜角为45°，对于任意的 ‎，函数在区间上总不是单调函数，求的取值范围．‎ 醴陵二中，醴陵四中 ‎2017年下学期两校联考高二年级数学（文）科期末考试试卷 命题学校：醴陵二中 命题人：贺建军 审题人：宁盼 ‎（时间120分钟，满分150分）‎ 一、选择题：（每小题5分，共计60分）‎ ‎1、若将复数表示为，是虚数单位)的形式,则的值为( A )‎ ‎ A．-2 B． C．2 D． ‎ ‎2、给出如下四个命题：‎ ‎①若“或”为假命题，则，均为假命题；‎ ‎②命题“若且，则”的否命题为“若，则”； ‎ ‎③在中，“”是“”的充要条件；‎ ‎④命题“若”的逆否命题为真命题。其中正确命题的个数是（ B ）‎ ‎ A．3 B．2 C．1 D．0‎ ‎3、已知变量之间具有线性相关关系，其散点图如图所示，则其回归方程可能为（ D ）‎ A. B. ‎ C. D. ‎ ‎4、已知双曲线的离心率为，则的渐近线方程为（ C ）‎ A． B． C． D．‎ ‎5、下面四个条件中,使成立的充分不必要的条件是（ B ）‎ A. B. C. D. ‎ ‎6、已知，则函数是(　D　)‎ A．仅有最小值的奇函数 B．既有最大值又有最小值的偶函数 C．仅有最大值的偶函数 D．既有最大值又有最小值的奇函数 ‎7、某种树的分枝生长规律如图所示，第1年到第5年的分枝数分别为1,1,2,3,5，则预计第10年树的分枝数为(　D　)‎ A．21 B．34 C．52 D．55‎ ‎8、如图所示的工序流程图中，设备采购的下一道工序是(　A　)‎ A．设备安装 B．土建设计 C．厂房土建 D．工程设计 ‎9、若，则双曲线的离心率的取值范围（ C ）‎ A、 B、 C、 D、‎ ‎10、若关于x的方程在区间上仅有一个实根，则实数的取值范围为（ C ）‎ A． B． ‎ C． D．‎ ‎11、下面四个推导过程符合演绎推理三段论形式且推理正确的是( B )‎ A．大前提：无限不循环小数是无理数；小前提：π是无理数；结论：π是无限不循环小数 B．大前提：无限不循环小数是无理数；小前提：π是无限不循环小数；结论：π是无理数 C．大前提：π是无限不循环小数；小前提：无限不循环小数是无理数；结论：π是无理数 D．大前提：π是无限不循环小数；小前提：π是无理数；结论：无限不循环小数是无理数 ‎12、当时，不等式恒成立，则实数的取值范围是（ A ）‎ A． B． C． D． ‎ 二、填空题（每小题5分，共20分）‎ ‎13、已知命题“，使”是假命题，则实数的取值范围是 ‎ ‎ ‎14、函数的图象在点处的切线方程为,为的导函数，则___4____‎ ‎15、已知椭圆的中心在坐标原点，离心率为，的右焦点与抛物线的焦点重合，是的准线与椭圆的两个交点，则 6 .‎ ‎16、已知f (x)＝x3－6x2＋9x－abc，a＜b＜c，且f (a)＝f (b)＝f (c)＝0.现给出如下结论：①f(0)f(1)＞0; ②f(0)f(1)＜0； ③f(0)f(3)＞0; ④f(0)f(3)＜0.‎ 其中正确结论的序号是__②③______．‎ 三、解答题：（共70分）‎ ‎17、（本小题满分10分）设是实数,已知命题函数的最小值小于；已知命题： “方程表示焦点在轴上的椭圆”，若为真命题，为假命题，求实数的取值范围。‎ 解： 2分 ‎ 4分 真假 6分 假真 8分 综上得的范围是或 10分 ‎18、（本小题满分12分）已知抛物线，过点引一条弦使它恰好被点平分，求这条弦所在的直线方程及.‎ 解:设直线上任意一点坐标为(x，y)，弦两端点P1(x1，y1)，P2(x2，y2)．‎ ‎∵P1，P2在抛物线上，∴y＝6x1，y＝6x2.‎ 两式相减，得(y1＋y2)(y1－y2)＝6(x1－x2)． 3分 ‎∵y1＋y2＝2，∴k＝＝＝3.‎ ‎∴直线的方程为y－1＝3(x－2)，即3x－y－5＝0. 6分 ‎ ∴‎ ‎∴y1＋y2＝2，y1·y2＝－10. 9分 ‎∴|P1P2|＝ ＝. 12分 ‎19、( 本小题满分12分)某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主). ‎ ‎(1)根据茎叶图,帮助这位同学说明这30位亲属的饮食习惯.‎ ‎(2)根据以上数据完成如下2×2列联表.‎ 主食蔬菜 主食肉类 总计 ‎50岁以下 ‎50岁以上 总计 ‎(3)能否有99％的把握认为其亲属的饮食习惯与年龄有关?‎ ‎ ‎ ‎[解析] (1)由茎叶图可知,30位亲属中50岁以上的人饮食多以蔬菜为主,50岁以下的人饮食多以肉类为主. 4分 ‎(2) 2×2列联表如下所示:‎ 主食蔬菜 主食肉类 总计 ‎50岁以下 ‎4‎ ‎8‎ ‎12‎ ‎50岁以上 ‎16‎ ‎2‎ ‎18‎ 总计[来源:Zxxk.Com]‎ ‎20‎ ‎10‎ ‎30‎ ‎ 8分 ‎(3)由题意,随机变量的观测值 故有99％的把握认为其亲属的饮食习惯与年龄有关. 12分 ‎20、(本小题满分分)已知函数，当和时，取得极值．‎ ‎(1)求的值； ‎ ‎(2)若函数的极大值大于20，极小值小于5，试求的取值范围．‎ 解:(1)f′(x)＝3x2＋2bx＋c，∵当x＝－3和x＝1时，f(x)取得极值，‎ ‎∴f′(－3)＝0，f′(1)＝0.‎ ‎∴解得b＝3，c＝－9. 6分 ‎(2)由(1)知：f(x)＝x3＋3x2－9x＋d， f′(x)＝3x2＋6x－9，‎ 令f′(x)>0，得3x2＋6x－9>0，解得x<－3，或x>1， 8分 ‎∴当x变化时，f′(x)，f(x)的变化情况如下表：‎ x ‎(－∞，－3)‎ ‎－3‎ ‎(－3,1)‎ ‎1‎ ‎(1，＋∞)‎ f′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ ↗‎ 极大值27＋d ↘‎ 极小值d－5‎ ↗ ‎ 10分 ‎∵函数f(x)的极大值大于20，极小值小于5，‎ ‎∴解得－7

查看更多