【数学】2019届一轮复习北师大版几何体与球切、接的问题学案

【数学】2019届一轮复习北师大版几何体与球切、接的问题学案

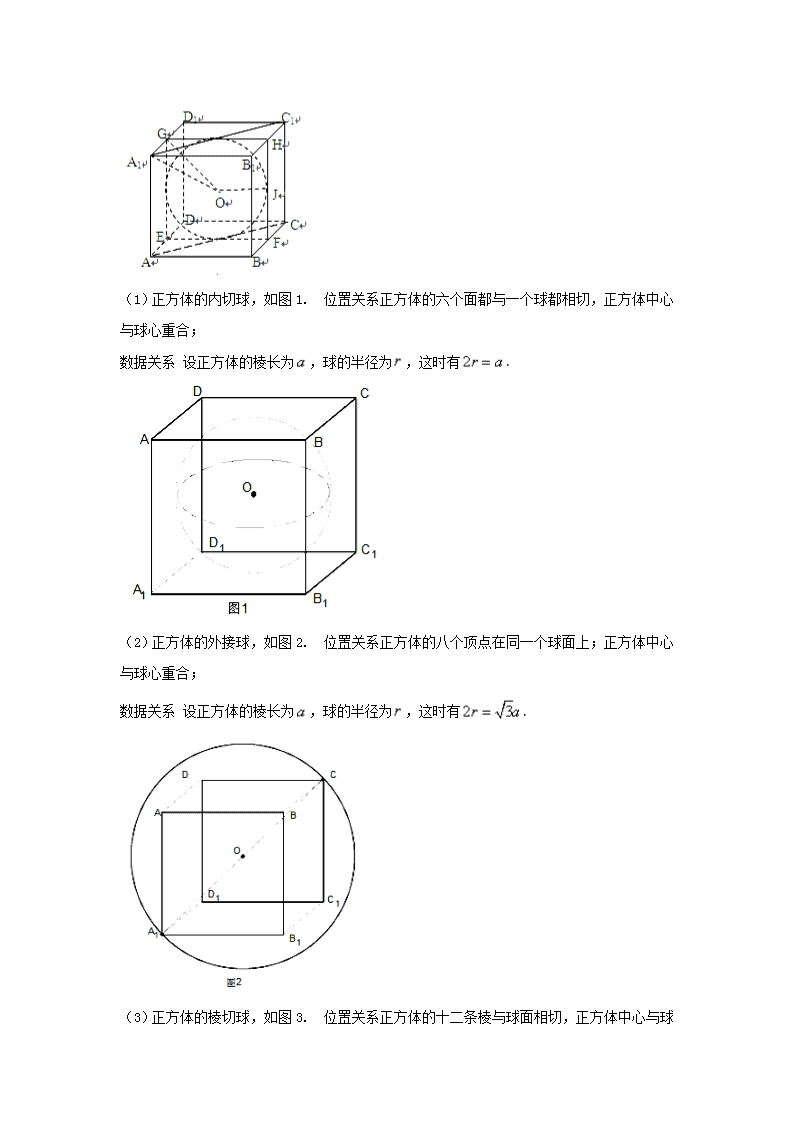
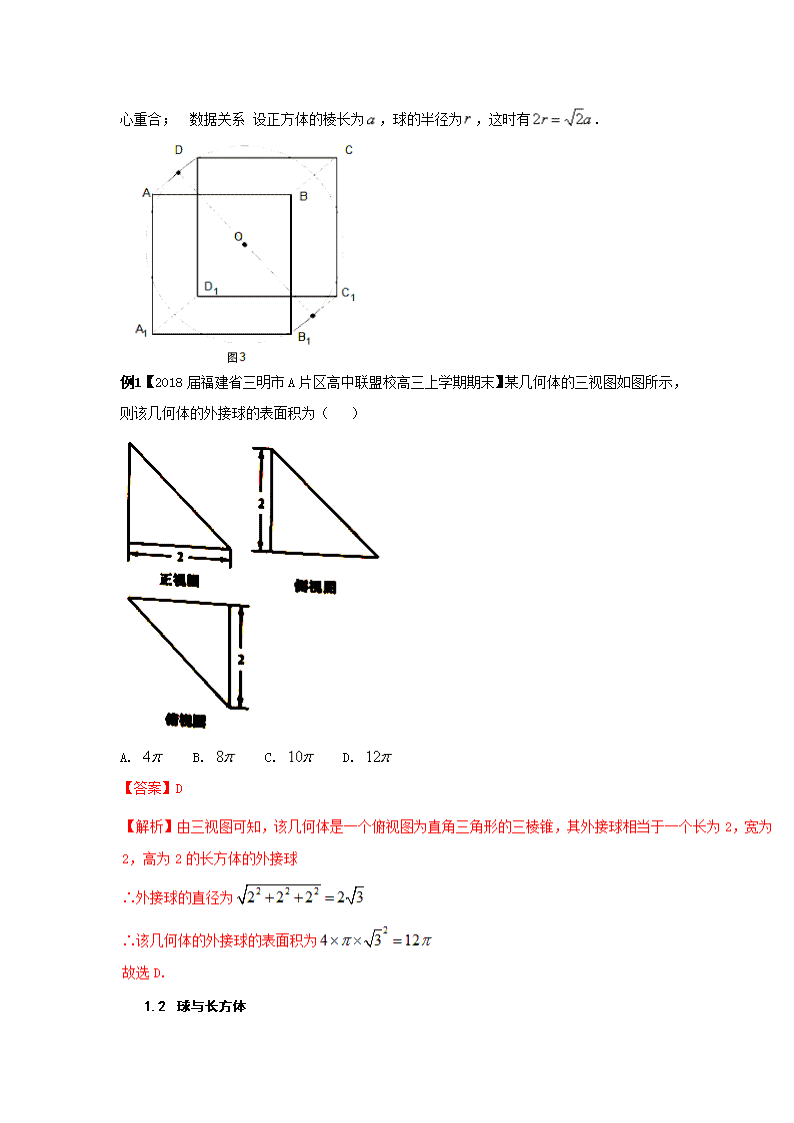
热点七 几何体与球切、接的问题 ‎ 纵观近几年高考对于组合体的考查，与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显，要求学生有较强的空间想象能力和准确的计算能力，才能顺利解答.从实际教学 看，这部分知识学生掌握较为薄弱、认识较为模糊，看到就头疼的题目.分析原因，除了这类题目的入手确实不易之外，主要是学生没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理. 下面结合近几年高考题对球与几何体的切接问题作深入的探究,以便更好地把握高考命题的趋势和高考的命题思路,力争在这部分内容不失分.从近几年全国高考命题 看,这部分内容以选择题、填空题为主，大题很少见. ‎ 首先明确定义1 若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。‎ 定义2 若一个多面体的各面都与一个球的球面相切， 则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.‎ ‎1 球与柱体的切接 ‎ 规则的柱体，如正方体、长方体、正棱柱等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱柱的棱产生联系，然后考查几何体的体积或者表面积等相关问题.‎ 1.1 ‎ 球与正方体 ‎ 如图所示，正方体，设正方体的棱长为，为棱的中点，为球的球心.常见组合方式有三类 一是球为正方体的内切球，截面图为正方形和其内切圆，则；二是与正方体各棱相切的球，截面图为正方形和其外接圆，则；三是球为正方体的外接球，截面图为长方形和其外接圆，则.通过这三种类型可以发现，解决正方体与球的组合问题，常用工具是截面图，即根据组合的形式找到两个几何体的轴截面，通过两个截面图的位置关系，确定好正方体的棱与球的半径的关系，进而将空间问题转化为平面问题.‎ ‎（1）正方体的内切球，如图1. 位置关系 正方体的六个面都与一个球都相切，正方体中心与球心重合； ‎ 数据关系 设正方体的棱长为，球的半径为，这时有. ‎ ‎（2）正方体的外接球，如图2. 位置关系 正方体的八个顶点在同一个球面上；正方体中心与球心重合； ‎ 数据关系 设正方体的棱长为，球的半径为，这时有.‎ ‎（3）正方体的棱切球，如图3. 位置关系 ‎ 正方体的十二条棱与球面相切，正方体中心与球心重合； 数据关系 设正方体的棱长为，球的半径为，这时有.‎ 例 1【2018届福建省三明市A片区高中联盟校高三上学期期末】某几何体的三视图如图所示，则该几何体的外接球的表面积为（ ） ]‎ A. B. C. D. ‎ ‎【答案】D 1.1 球与长方体 例 2 自半径为的球面上一点，引球的三条两两垂直的弦，求的值．‎ ‎【答案】.‎ ‎【解析】以为从一个顶点出发的三条棱，将三棱锥补成一个长方体，则另外四个顶点必在球面上，故长方体是球的内接长方体，则长方体的对角线长是球的直径． ‎ ‎=．‎ 例 3【2018届二轮复习专题】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥PABC为鳖臑，PA⊥平面ABC，PA＝AB＝2，AC＝4，三棱锥PABC的四个顶点都在球O的球面上，则球O的表面积为(　　)‎ A. 8π B. 12π C. 20π D. 24π ‎【答案】C ‎2 球与锥体的切接 ‎ 规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题.‎ ‎2.1正四面体与球的切接问题 ‎ ‎ （1） 正四面体的内切球，如图4. 位置关系 ‎ 正四面体的四个面都与一个球相切，正四面体的中心与球心重合；  ‎ ‎ 数据关系 设正四面体的棱长为，高为；球的半径为，这时有；（可以利用体积桥证明） ‎ ‎ （2） 正四面体的外接球，如图5. 位置关系 正四面体的四个顶点都在一个球面上，正四面体的中心与球心重合； ‎ ‎ 数据关系 设正四面体的棱长为，高为；球的半径为，这时有；（可用正四面体高减去内切球的半径得到）‎ ‎ ‎ ‎ （3） 正四面体的棱切球，如图6. 位置关系 正四面体的六条棱与球面相切，正四面体的中心与球心重合； ‎ ‎ 数据关系 设正四面体的棱长为，高为；球的半径为，这时有 ‎ 例 4【2018届广西防城港市高三1月模拟】各面均为等边三角形的四面体的外接球的表面积为，过棱作球的截面，则截面面积的最小值为__________．‎ ‎【答案】‎ ‎【解析】将四面体放回一个正方体中,使正四面体的棱都是正方体的面对角线,那么正四面体和正方体的外接球是同一个球,当AB是截面圆的直径时,截面面积最小.‎ 因外接球的表面积为,则球的直径为,则正方体的体对角线为,棱长为1,面对角线为,截面圆面积最小值为.‎ 点评 与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图.‎ ‎2.2其它棱锥与球的切接问题 ‎ 球与正棱锥的组合，常见的有两类，一是球为三棱锥的外接球，此时三棱锥的各个顶点在球面上，根据截面图的特点，可以构造直角三角形进行求解.二是球为正棱锥的内切球，例如正三棱锥的内切球，球与正三棱锥四个面相切，球心到四个面的距离相等，都为球半径．这样求球的半径可转化为球球心到三棱锥面的距离，故可采用等体积法解决，即四个小三棱锥的体积和为正三棱锥的体积.‎ ‎ 球与一些特殊的棱锥进行组合，一定要抓住棱锥的几何性质，可综合利用截面法、补形法等进行求解.例如，四个面都是直角三角形的三棱锥，可利用直角三角形斜边中点几何特征，巧定球心位置.‎ 例5【湖南省长沙市长郡中学2017届高三摸底】已知边长为的菱形中，‎ ‎，沿对角线折成二面角为的四面体，则四面体的外接球的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】D 例6【江西省新余市第一中学2017届高三上学期调研考试（一）】某几何体的正视图和侧视图如图（1）所示, 它的府视图的直观图是,如图（2）所示, 其中,则该几何体的外接球的表面积为 ．‎ ‎ ‎ ‎【答案】‎ ‎【解析】‎ 由斜二测画法易知，该几何体的俯视图是一个边长为4的等边三角形,再结合正视图和侧视图可知，该几何体是如下图所示的高为4的三棱锥D－ABC，将其补形为三棱柱 ABC-EDF,设球心为O，的中心为，则,所以该几何体的外接球的半径,其表面积为.‎ 例7【2018届山西省太原十二中高三上学期1月】在四棱锥中， 底面，底面为正方形， ， ，记四棱锥的外接球与三棱锥的外接球的表面积分别为，则___．‎ ‎【答案】‎ ‎【解析】设正方形的边长为，设为的中点，因为平面，而平面，所以，又，故，又，故平面， 平面，所以，故为直角三角形， 为斜边，所以．同理也为直角三角形，结合 ，所以，又， ，所以平面， 平面，所以， 为直角三角形，所以， 为三棱锥 外接球的球心，且半径．同理设为 的中点，则为四棱锥外接球的球心，且半径，所以．填．‎ 点睛 球的半径的计算，关键在球心位置的确定，三棱锥中均为直角三角形，因此外接球的球心就是的中点，因为它到四个顶点的距离是相等的．同理四棱锥外接球的球心就是的中点．‎ ‎3 球与球相切问题 ‎ 对于球与球的相切组合成复杂的几何体问题，要根据丰富的空间想象力，通过准确确定各个小球的球心的位置，或者巧借截面图等方法，将空间问题转化平面问题求解.‎ 例8 已知有半径分别为2、3的球各两个，且这四个球彼此相外切，现有一个球与此四个球都相外切，则此球 的半径为 .‎ ‎【答案】‎ ‎【解析】如图 设四个球的球心分别为A、B、C、D，则AD=AC=BD=BC=5，AB=6，CD=4.设AB中点为E、‎ CD中点为F，连结EF.在△ABF中求得BF=，在△EBF中求得EF=.‎ 由于对称性可得第五个球的球心O在EF上，连结OA、OD.设第五个球的半径为r，则OA=r+3，OD=r+2， ‎ 于是OE=，OF=，∵OE+OF=EF ‎∴平方整理再平方得 解得或（舍掉），故答案为.‎ 例9 把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与 ‎ 前三个都相切，求第四个球的最高点与桌面的距离．[ | ]‎ ‎【答案】.‎ 4 球与几何体的各条棱相切问题 ‎ 球与几何体的各条棱相切问题，关键要抓住棱与球相切的几何性质，达到明确球心的位置为目的，然后通过构造直角三角形进行转换和求解.如与正四面体各棱都相切的球的半径为相对棱的一半 .‎ 例10 把一个皮球放入如图10所示的由8根长均为20 cm的铁丝接成的四棱锥形骨架内，使皮球的表面与[ ]‎ ‎8根铁丝都有接触点，则皮球的半径为（ ）‎ A．l0cm B．10 cm C．10cm D．30cm ‎【答案】‎ ‎【解析】如图所示，由题意球心在AP上，球心为O，过O作BP的垂线ON垂足为N，ON=R，OM=R，因为各个棱都为20，所以AM=10，BP=20,BM=10，AB=,设，‎ 在BPM中，,所以.在PAM中, ,所以 ‎.在ABP中, ，在ONP中, ,所以 ‎，所以.在OAM中, ,所以，‎ ‎,解得，或30（舍）,所以，故选B.‎ ‎ ‎ 4 球与旋转体切接问题 ‎ 首先画出球及其它旋转体的公共轴截面，然后寻找几何体与几何体几何元素之间的关系．‎ 例11 求球与它的外切圆柱、外切等边圆锥的体积之比．学 ‎ ‎【答案】‎ ‎【解析】如图，等边为圆锥的轴截面，此截面截圆柱得正方形，截球面得球的大圆圆．‎ ‎ 设球的半径，则它的外切圆柱的高为，底面半径为；‎ ‎， ，[ ]‎ ‎∴，， ，‎ ‎∴．‎ ‎ ‎ 例12在棱长为1的正方体内有两个球相外切且又分别与正方体内切．（1）求两球半径之和；（2）球的半径 为多少时，两球体积之和最小．‎ ‎【答案】‎ ‎【解析】如图，球心和在上，过，分别作的垂线交于．‎ 则由得．‎ ‎， ．‎ ‎ ‎ ‎【反思提升】综合上面的五种类型，解决与球的外切问题主要是指球外切多面体与旋转体，解答时首先要找准切点，将问题转化成平面几何问题，应用三角形中的边角关系，建立与球半径的联系，将球的体积之和用或表示.如果外切的是多面体，则作截面时主要抓住多面体过球心的对角面 作；把一个多面体的几个顶点放在球面上即为球的内接问题．解决这类问题的关键是抓住内接的特点，即球心到多面体的顶点的距离等于球的半径．发挥好空间想象力，借助于数形结合进行转化，问题即可得解．如果是一些特殊的几何体，如正方体、正四面体等可以借助结论直接求解,此时结论的记忆必须准确.高考题往往与三视图相结合，题目的难易不一，在复习中切忌好高骛远，应重视各种题型的备考演练，重视高考信息的搜集，不断充实题目的类型，升华解题的境界.‎